
(a)
Interpretation:
Value of Yield strength at
Concept introduction:
Elastic modulus is defined as the ratio of shear stress to shear strain. It is denoted by E, the relationship is given as,
Stress is defined as the ratio of load per unit area. It is denoted by
Where,
P is the force in newton.
A is area in square meter.
Strain is defined as the ratio of change in length to original length. It is denoted by
Where,
Strain is dimensionless quantity.
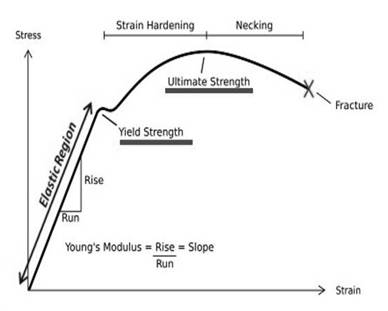
Offset is defined as the yield point in stress strain curve. The figure represents the Stress-Strain curve,
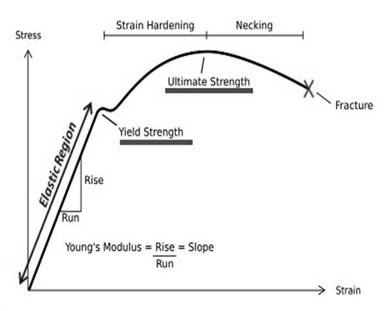
Answer to Problem 6.36P
The requiredvalue of Yield strength at
Explanation of Solution
Given information:
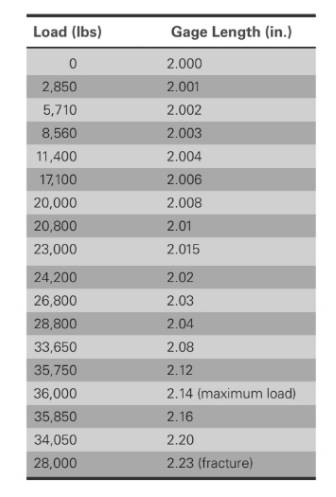
The data for AISI-SAE stainless steel is given below:
Diameter of stainless steel is
Gage length before fracture is
After fracture, the given values are,
Gage length after fracture is
Diameter of stainless steel is
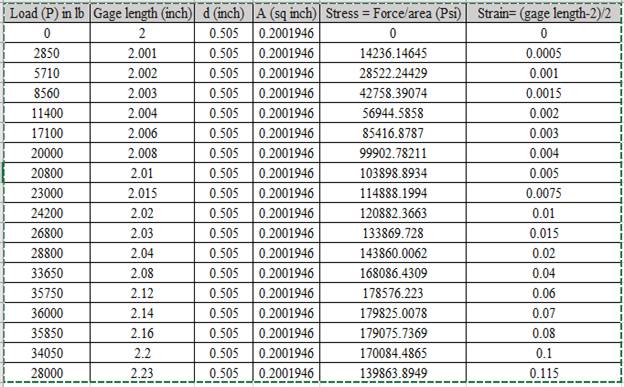
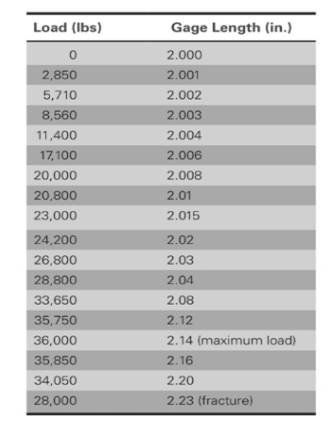
The values of load correspond to gage length is shown in table,
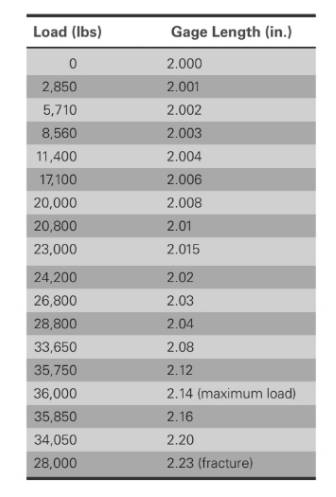
Based on given information
Applying formula of elastic modulus,
Stress is calculated on the basis on force and area. The given formula is,
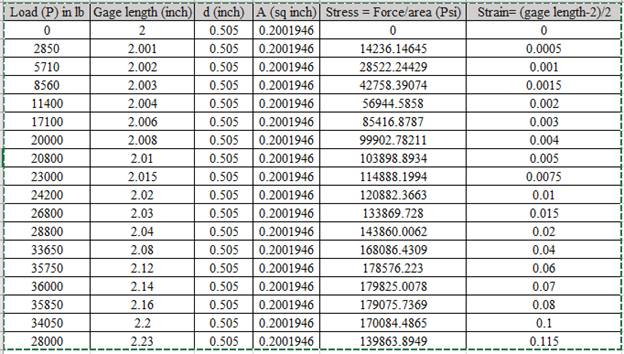
Calculation of stress and strain values are done using spreadsheet shown below,
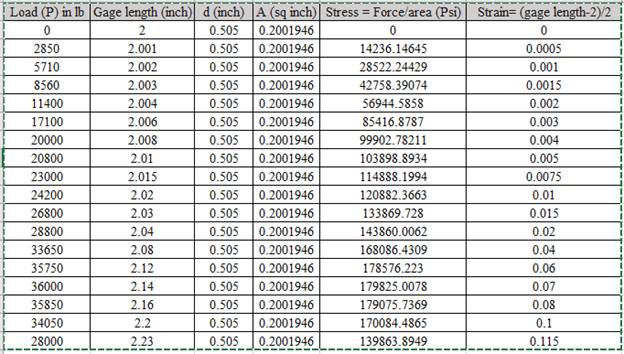
Using the data for Stress-Strain, Drawing the Stress Strain curve,
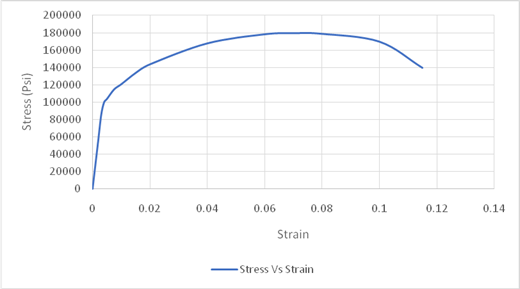
As, the value of offset is given in percentage so converting percentage by dividing it with
Drawing the tie line at offset of
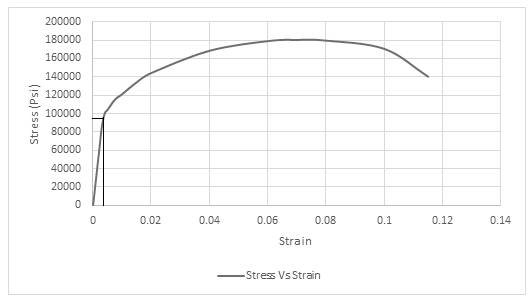
Thus, the required value of yield strength is
(b)
Interpretation:
The value of tensile strength for the given condition is to be determined.
Concept introduction:
Elastic modulus is defined as the ratio of shear stress to shear strain. It is denoted by E, the relationship is given as,
Stress is defined as the ratio of force per unit area. It is denoted by
Where,
F is the force in newton.
A is area in square meter.
Strain is defined as the ratio of change in length to original length. It is denoted by
Where,
Strain is dimensionless quantity.
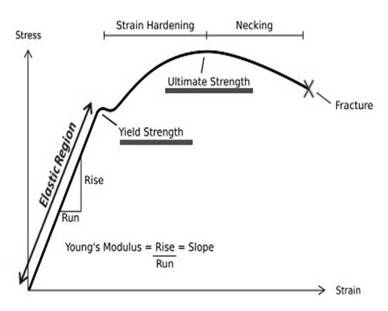
Tensile strength is the maximum load that material can withstand without rapture. The above graph is reflecting relationship between stress and strain.
Answer to Problem 6.36P
Thus, the required value of tensile strength is
Explanation of Solution
Given information:
The data for AISI-SAE stainless steel is given below:
Diameter of stainless steel is
Gage length before fracture is
After fracture, the given values are,
Gage length after fracture is
Diameter of stainless steel is
The values of load correspond to gage length is shown in table,
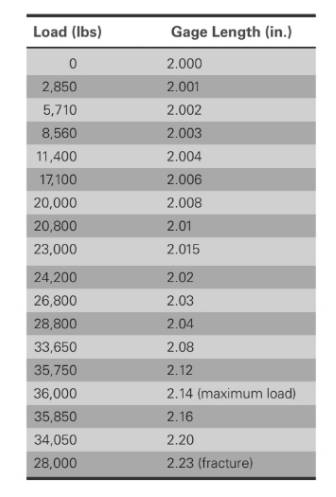
Based on given information
Applying formula of elastic modulus,
Stress is calculated on the basis on force and area. The given formula is,
Calculation of stress and strain values are done using spreadsheet shown below,
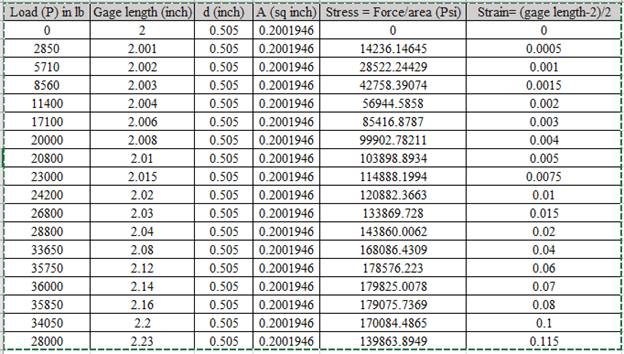
Using the data for Stress-Strain, Drawing the Stress Strain curve,
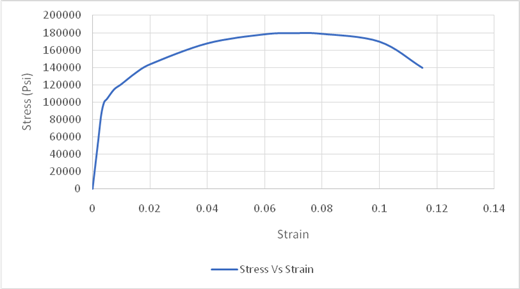
The maximum value of stress is used for obtaining the value of tensile strength. Drawing tie lines as shown in the figure below,
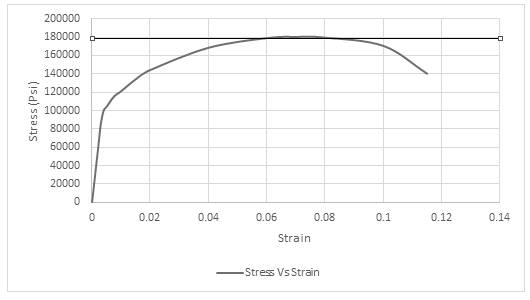
Thus, the required value of tensile strength is
(c)
Interpretation:
The value of Modulus of elasticity for the given condition should be calculated.
Concept introduction:
Elastic modulus is defined as the ratio of shear stress to shear strain. It is denoted by E, the relationship is given as,
Stress is defined as the ratio of force per unit area. It is denoted by
Where,
F is the force in newton.
A is area in square meter.
Strain is defined as the ratio of change in length to original length. It is denoted by
Where,
Strain is dimensionless quantity.
The graph of Proportionality constant using modulus of elasticity,
Answer to Problem 6.36P
Thus, the required value of modulus of elasticity is
Explanation of Solution
Given information:
The data for AISI-SAE stainless steel is given below:
Diameter of stainless steel is
Gage length before fracture is
After fracture, the given values are,
Gage length after fracture is
Diameter of stainless steel is
The values of load correspond to gage length is shown in table,
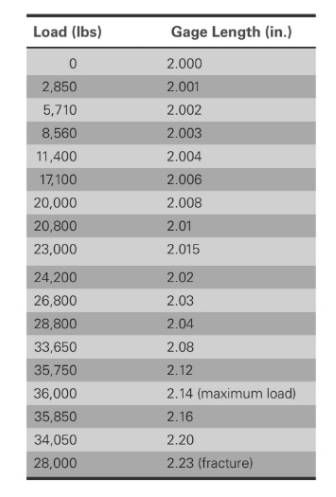
Based on given information
Applying formula of elastic modulus,
Stress is calculated on the basis on force and area. The given formula is,
Calculation of stress and strain values are done using spreadsheet shown below,
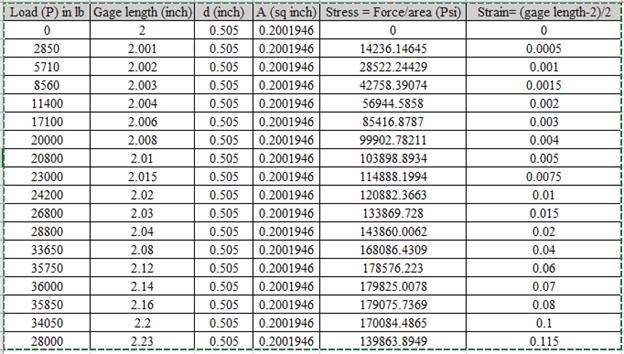
Using the data for Stress-Strain, Drawing the Stress Strain curve,
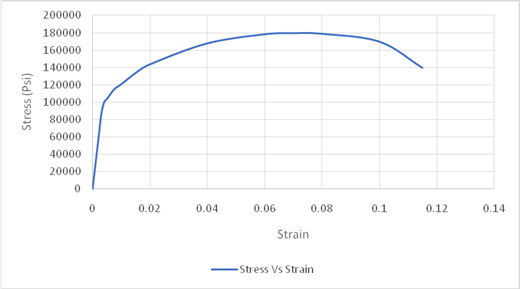
For calculating the modulus of elasticity, the values considered are highlighted in spreadsheet,
Using the above table the value of stress is
Calculation of modulus of elasticity,
Putting the values in formula,
Thus, the required value of modulus of elasticity is
(d)
Interpretation:
The value of percentage elongation for the given condition should be calculated.
Concept introduction:
Stress is defined as the ratio of force per unit area. It is denoted by
Where,
F is the force in newton.
A is area in square meter.
Strain is defined as the ratio of change in length to original length. It is denoted by
Where,
Strain is dimensionless quantity.
Percentage elongation:
It is defined as the ratio of difference between final length and initial length to initial length. The relationship is given as,
Where,
Answer to Problem 6.36P
Thus, the required value of percentage elongation is
Explanation of Solution
Given information:
The data for AISI-SAE stainless steel is given below:
Diameter of stainless steel is
Gage length before fracture is
After fracture, the given values are,
Gage length after fracture is
Diameter of stainless steel is
The values of load correspond to gage length is shown in table,
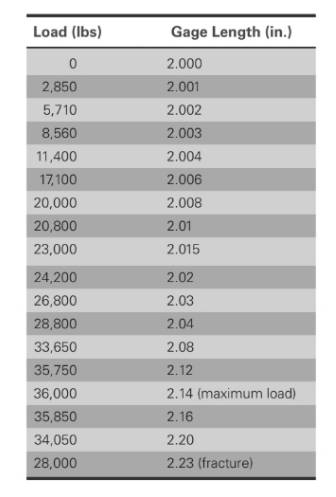
Based on the values,
Gage length before fracture is
Gage length after fracture is
Putting the values in the formula of percentage elongation,
Thus, the required value of percentage elongation is
(e)
Interpretation:
The value of percentage reduction in area for given condition should be calculated.
Concept introduction:
Stress is defined as the ratio of force per unit area. It is denoted by
Where,
F is the force in newton.
A is area in square meter.
Strain is defined as the ratio of change in length to original length. It is denoted by
Where,
Strain is dimensionless quantity.
True Strain: It is defined as the ratio of gage length to instantaneous gage length. The formula is given below:
Where,
Percentage Reduction in Area:
It is defined as the ratio of difference between final length and initial length to initial length. The relationship is given as,
Where,
Answer to Problem 6.36P
The required value of percentage reduction in area is
Explanation of Solution
Given information:
The data for AISI-SAE stainless steel is given below:
Diameter of stainless steel is
Gage length before fracture is
After fracture, the given values are,
Gage length after fracture is
Diameter of stainless steel is
The values of load correspond to gage length is shown in table,
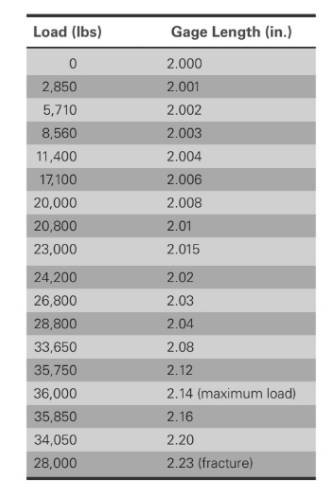
Based on the given values,
Calculation of
Calculation of
Substituting the values in the formula of percentage reduction of area,
The required value of percentage reduction in area is
(f)
Interpretation:
The value of engineering stress at fracture should be determined.
Concept introduction:
Stress is defined as the ratio of force per unit area. It is denoted by
Where,
F is the force in newton.
A is area in square meter.
Strain is defined as the ratio of change in length to original length. It is denoted by
Where,
Strain is dimensionless quantity.
Answer to Problem 6.36P
Thus, the required value of Stress at fracture is
Explanation of Solution
Given information:
The data for AISI-SAE stainless steel is given below:
Diameter of stainless steel is
Gage length before fracture is
After fracture, the given values are,
Gage length after fracture is
Diameter of stainless steel is
The values of load correspond to gage length is shown in table,
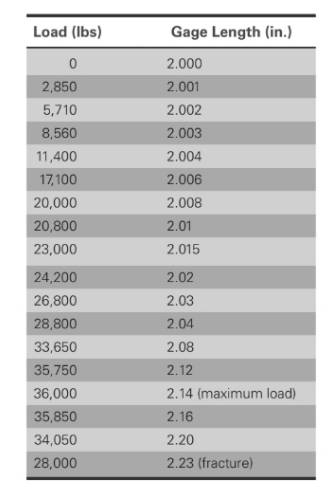
Based on the given values,
Based on given information
Applying formula of elastic modulus,
Stress is calculated on the basis on force and area. The given formula is,
Calculation of stress and strain values are done using spreadsheet shown below,
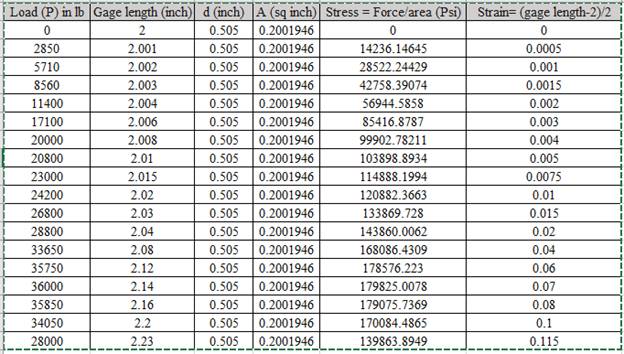
Using the data for Stress-Strain, Drawing the Stress Strain curve,
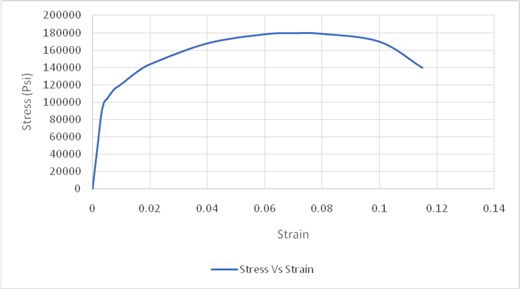
Drawing the tie lie at the fracture point of Stress-Strain curve,
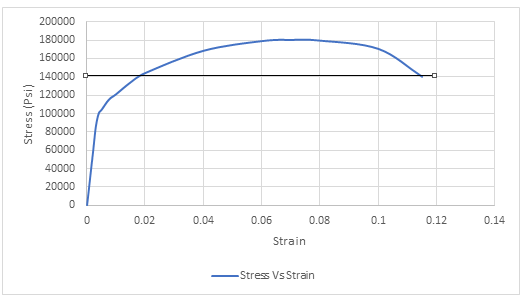
Thus, the required value of Stress at fracture is
(g)
Interpretation:
The value of true stress at necking should be calculated.
Concept introduction:
Stress is defined as the ratio of force per unit area. It is denoted by
Where,
F is the force in newton.
A is area in square meter.
Strain is defined as the ratio of change in length to original length. It is denoted by
Where,
Strain is dimensionless quantity.
True stress is defined as the ratio of force per unit area. The relationship is given as,
Where,
Answer to Problem 6.36P
Thus, the required value of true stress at neck point is
Explanation of Solution
Given information:
The data for AISI-SAE stainless steel is given below:
Diameter of stainless steel is
Gage length before fracture is
After fracture, the given values are,
Gage length after fracture is
Diameter of stainless steel is
The values of load correspond to gage length is shown in table,
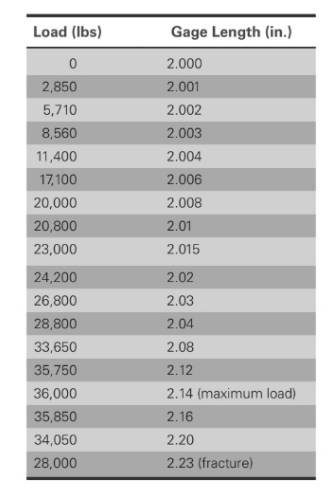
Based on the given values,
The different values of stress, Strain, gage diameter is shown below:
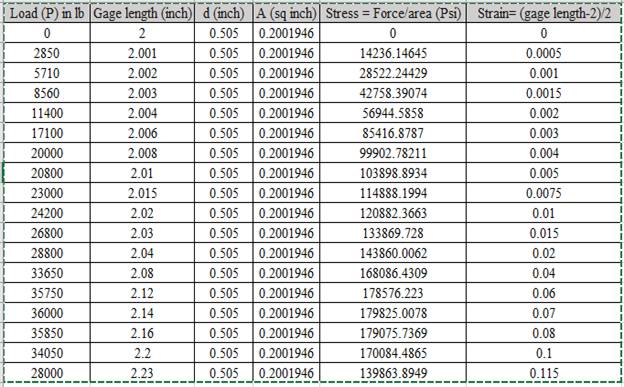
Calculation of true stress:
Following points are considered for calculating the values of true stress at gage length of
Calculation of area,
Calculation of strain,
Putting the values in the formula of true stress,
Thus, the required value of true stress at neck point is
(h)
Interpretation:
The value of Modulus of resilience for the given condition should be calculated.
Concept introduction:
Stress is defined as the ratio of force per unit area. It is denoted by
Where,
F is the force in newton.
A is area in square meter.
Strain is defined as the ratio of change in length to original length. It is denoted by
Where,
Strain is dimensionless quantity.
Modulus of Resilience is defined as the maximum amount of energy that a material can withstand without creating the permanent distortion of the material.
The relationship of Modulus of Resilience is,
Where,
The graph is showing the values of yield stress and strain corresponding to the yield value,
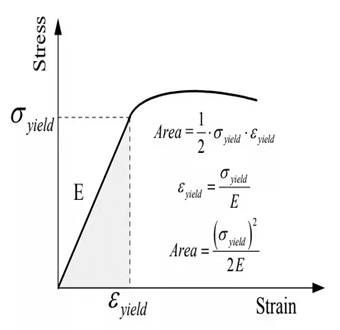
Answer to Problem 6.36P
Thus, the required value of modulus of resilience is
Explanation of Solution
Given information:
The data for AISI-SAE stainless steel is given below:
Diameter of stainless steel is
Gage length before fracture is
After fracture, the given values are,
Gage length after fracture is
Diameter of stainless steel is
The values of load correspond to gage length is shown in table,
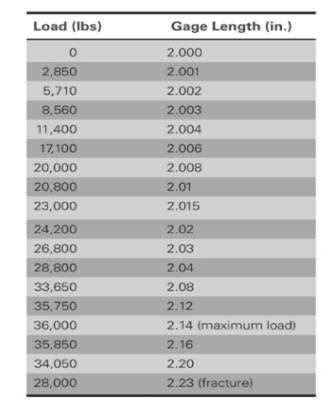
Based on the given values,
The different values of stress, Strain, gage diameter is shown below:
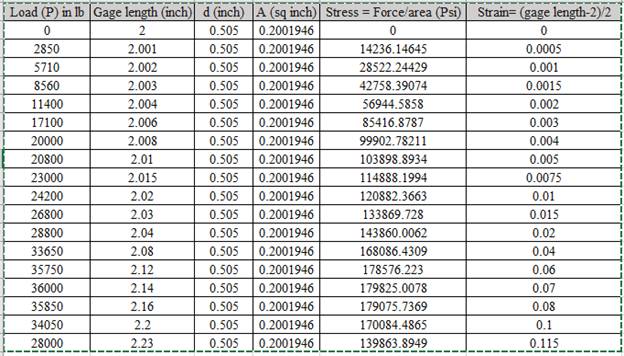
Based on the calculated values of stress and strain. The graph is shown below,
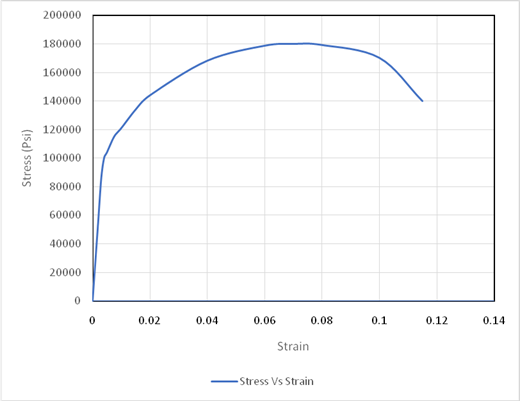
Using the above graph drawing tie lines,
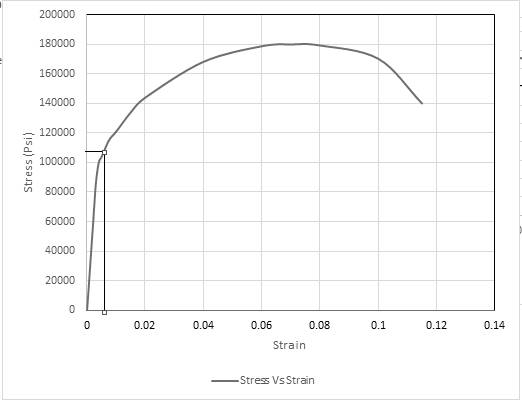
Thus, based on the tie line, The value for yield stress is
Substituting the values for calculating the modulus of resilience,
Thus, the required value of modulus of resilience is
(i)
Interpretation:
The value of elastic and plastic strain corresponding to fracture should be determined.
Concept introduction:
Elastic strainis defined as the distortion in the structure.
Plastic Strain is defined as the permanent distortion of structure.
The graph for elastic and plastic strain is shown below:
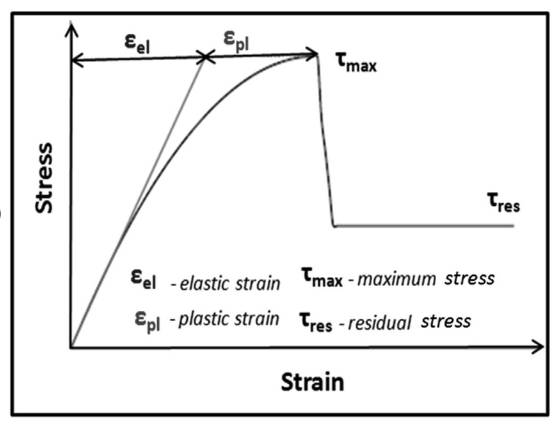
Answer to Problem 6.36P
Thus, the required value of elastic strain is
Thus, the required value of plastic strain is
Explanation of Solution
Given information:
The data for AISI-SAE stainless steel is given below:
Diameter of stainless steel is
Gage length before fracture is
After fracture, the given values are,
Gage length after fracture is
Diameter of stainless steel is
The values of load correspond to gage length is shown in table,
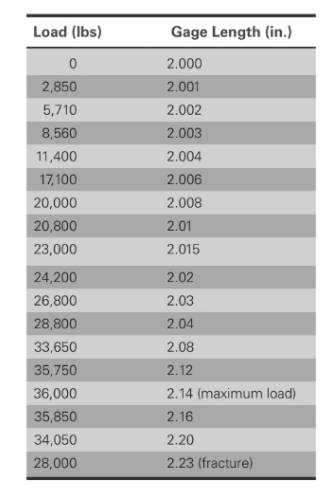
Based on the given values,
The different values of stress, Strain, gage diameter is shown below:
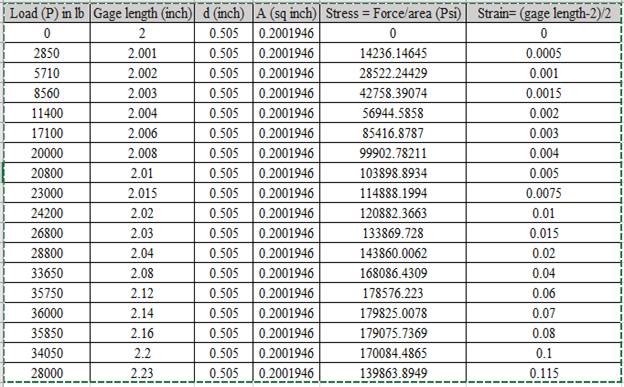
Based on the given values.
Plotting the graph,
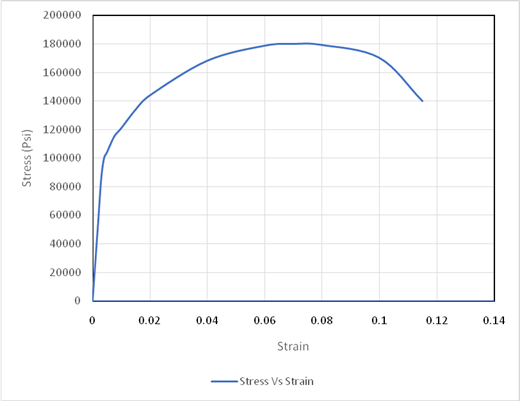
Based on given information
Applying formula of elastic modulus,
Stress is calculated on the basis on force and area. The given formula is,
For calculating the modulus of elasticity, the values considered are highlighted in spreadsheet,
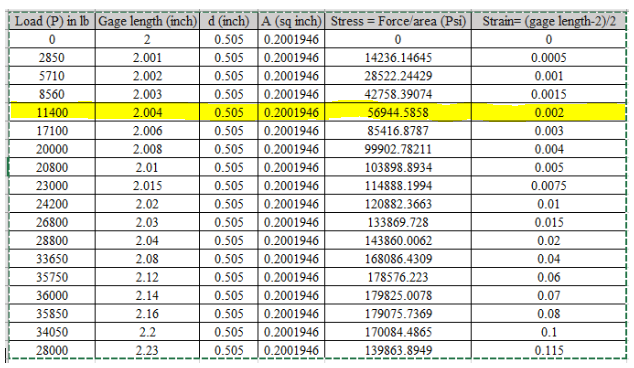
Using the above table the value of stress is
Putting the value of modulus of elasticity and stress,
Calculation of elastic strain,
Putting the values in formula,
Thus, the required value of elastic strain is
Using graph, drawing tie lines for determining the value of plastic strain,
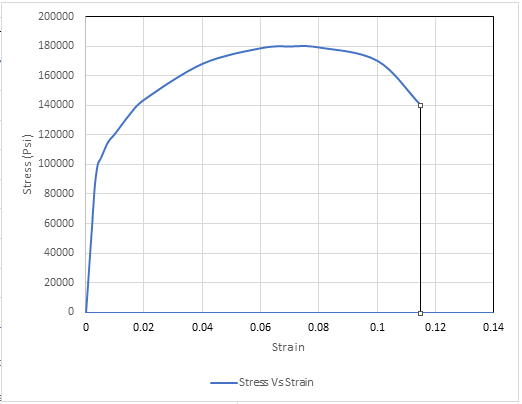
Thus, the required value of plastic strain is
(j)
Interpretation:
The transverse and axial strain for given condition should be determined. Also, the value of Poisson's ratio is to be calculated.
Concept introduction:
Transverse Strain is defined as the ratio of change in diameter to original diameter. The relationship is given as,
Where,
d is the original diameter.
Axial Strain is defined as the ratio of change in length to original length. It is denoted by
Where,
Strain is dimensionless quantity.
Poisson's Ratio:
It is defined as the ratio of transverse strain to axial strain represented as:
Answer to Problem 6.36P
The required value of transverse strain is
Thus, the required value of axial strain is
The required value of Poisson's ratio is
Explanation of Solution
Given information:
The data for AISI-SAE stainless steel is given below:
Diameter of stainless steel is
Gage length before fracture is
After fracture, the given values are,
Gage length after fracture is
Diameter of stainless steel is
The values of load correspond to gage length is shown in table,
Load for sample is
Diameter of sample is
Based on the given values,
The different values of stress, Strain, gage diameter is shown below:
Calculation of transverse strain,
Where,
Putting the values,
The required value of transverse strain is
Calculation of axial strain,
Where,
Thus, the required value of axial strain is
Calculation of Poisson's ratio,
Putting the value of transverse and axial strain,
Thus, the required value of Poisson's ratio is
(k)
Interpretation:
The value of tensile strength for 416 stainless steel is to be determined. Also, the comparison of values for tensile strength should be explained.
Concept introduction:
Elastic modulus is defined as the ratio of shear stress to shear strain. It is denoted by E, the relationship is given as,
Stress is defined as the ratio of force per unit area. It is denoted by
Where,
F is the force in newton.
A is area in square meter.
Strain is defined as the ratio of change in length to original length. It is denoted by
Where,
Strain is dimensionless quantity.
Tensile strength is the maximum load that material can withstand without rapture. The above graph is reflecting relationship between stress and strain.
Answer to Problem 6.36P
Thus, the required calculated value of tensile strength is
Thus, the value of tensile strength remains the same after quenching and tempering.
Explanation of Solution
Given information:
The data for AISI-SAE stainless steel is given below:
Diameter of stainless steel is
Gage length before fracture is
After fracture, the given values are,
Gage length after fracture is
Diameter of stainless steel is
The values of load correspond to gage length is shown in table,
Load for sample is
Diameter of sample is
Based on given information
Applying formula of elastic modulus,
Stress is calculated on the basis on force and area. The given formula is,
Calculation of stress and strain values are done using spreadsheet shown below,
Using the data for Stress-Strain, Drawing the Stress Strain curve,
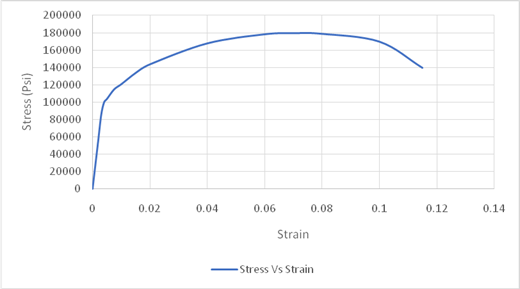
The maximum value of stress is used for obtaining the value of tensile strength. Drawing tie lines as shown in the figure below,
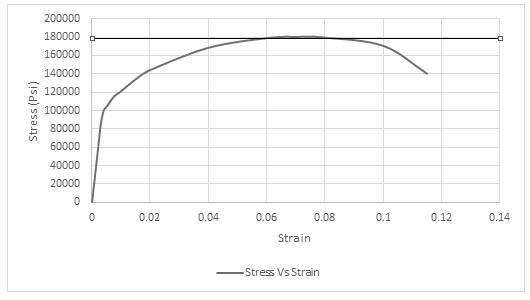
Thus, the required value of tensile strength is
Based on the given information the physical and mechanical properties of 416 stainless steel is shown below:
Thus, the required calculated value of tensile strength is
Thus, the required calculated value of yield strength is
The values of 416 stainless steel when quenched and tempered is shown in table,
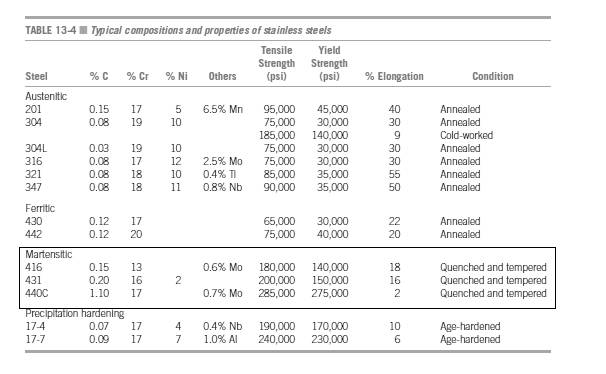
Thus, the value of tensile strength remains the same after quenching and tempering.
Want to see more full solutions like this?
Chapter 6 Solutions
Essentials Of Materials Science And Engineering
- the answer should be: V2= -(P0-PL/2μL)(dx-x^)+Ux/darrow_forwardFor some viscoelastic polymers that are subjected to stress relaxation tests, the stress decays with time according to a(t) = a(0) exp(-4) (15.10) where σ(t) and o(0) represent the time-dependent and initial (i.e., time = 0) stresses, respectively, and t and T denote elapsed time and the relaxation time, respectively; T is a time-independent constant characteristic of the material. A specimen of a viscoelastic polymer whose stress relaxation obeys Equation 15.10 was suddenly pulled in tension to a measured strain of 0.5; the stress necessary to maintain this constant strain was measured as a function of time. Determine E (10) for this material if the initial stress level was 3.5 MPa (500 psi), which dropped to 0.5 MPa (70 psi) after 30 s.arrow_forward1. Consider the following a unity feedback control system. R(s) + E(s) 500(s+2)(s+5)(s+6) s(s+8)(s+10)(s+12) -Y(s) Find the followings: a) Type of the system b) Static position error constant Kp, Static velocity error constant Ry and Static acceleration error constant Ka c) Find the steady-state error of the system for (i) step input 1(t), (ii) ramp input t 1(t), (iii) parabolic input t² 1(t). 2. Repeat the above problem for the following system. R(s) + E(s) 500(s + 2)(s + 5) (s+8)(s+ 10)(s+12) Y(s) 3. Repeat the above problem for the following system. R(s) + E(s) 500(s+2)(s+4)(s+5)(s+6)(s+7) s²(s+8)(s+10)(s+12) Y(s)arrow_forward
- For the flows in Examples 11.1 and 11.2, calculate the magnitudes of the Δ V2 / 2 terms omitted in B.E., and compare these with the magnitude of the ℱ terms.arrow_forward4. Consider a unity (negative) feedback control system whose open-loop transfer function is given by the following. 2 G(s) = s³ (s + 2) Find the steady-state error of the system for each of the following inputs. = a) u(t) (t²+8t+5) 1(t) b) u(t) = 3t³ 1(t) c) u(t) (t+5t² - 1) 1(t) =arrow_forward1 2. For the following closed-loop system, G(s) = and H(s) = ½ (s+4)(s+6) a. Please draw the root locus by hand and mark the root locus with arrows. Calculate the origin and angle for asymptotes. b. Use Matlab to draw the root locus to verify your sketch. Input R(s) Output C(s) KG(s) H(s)arrow_forward
- 5. Consider following feedback system. R(s) + 100 S+4 +1 Find the steady-state error for (i) step input and (ii) ramp input.arrow_forward6. Find (i) settling time (Ts), (ii) rise time (Tr), (iii) peak time (Tp), and (iv) percent overshoot (% OS) for each of the following systems whose transfer functions are given by: a) H(s) = 5 s²+12s+20 5 b) H(s) = s²+6s+25 c) H(s) = (s+2) (s²+12s+20) (s²+4s+13) Use dominant pole approximation if needed.arrow_forwardCalculate ℛP.M. in Example 11.2.arrow_forward
- For spherical sand particles with Dp = 0.03 and ρparticles = 150 lbm / ft3 estimate the minimum fluidizing velocity for air and for water. Assume ε = 0.3. In the case of the water we must rederive Eq. 11.42, taking into account the buoyant force on the particles. Below are the provide answers. Please show all work to get to the correct answers.arrow_forward7. Answer the following questions. Take help from ChatGPT to answer these questions (if you need). But write the answers briefly using your own words with no more than two sentences and make sure you check whether ChatGPT is giving you the appropriate answers in the context of class. a) Why do we need transient performance metrics? Name a few of such metrics. b) Define (i) settling time, (ii) rise time, (iii) peak time and (iv) percent overshoot. c) What is damping ratio? How does overshoot change with the change of damping ratio? When do we have zero overshoot? d) What is the criterion for selecting dominant pole in higher order systems? When dominant pole approximation is not valid? How will you calculate the transient performance metrics for the case when dominant pole approximation does not hold?arrow_forwardCan you help me with this problemarrow_forward
 MATLAB: An Introduction with ApplicationsEngineeringISBN:9781119256830Author:Amos GilatPublisher:John Wiley & Sons Inc
MATLAB: An Introduction with ApplicationsEngineeringISBN:9781119256830Author:Amos GilatPublisher:John Wiley & Sons Inc Essentials Of Materials Science And EngineeringEngineeringISBN:9781337385497Author:WRIGHT, Wendelin J.Publisher:Cengage,
Essentials Of Materials Science And EngineeringEngineeringISBN:9781337385497Author:WRIGHT, Wendelin J.Publisher:Cengage, Industrial Motor ControlEngineeringISBN:9781133691808Author:Stephen HermanPublisher:Cengage Learning
Industrial Motor ControlEngineeringISBN:9781133691808Author:Stephen HermanPublisher:Cengage Learning Basics Of Engineering EconomyEngineeringISBN:9780073376356Author:Leland Blank, Anthony TarquinPublisher:MCGRAW-HILL HIGHER EDUCATION
Basics Of Engineering EconomyEngineeringISBN:9780073376356Author:Leland Blank, Anthony TarquinPublisher:MCGRAW-HILL HIGHER EDUCATION Structural Steel Design (6th Edition)EngineeringISBN:9780134589657Author:Jack C. McCormac, Stephen F. CsernakPublisher:PEARSON
Structural Steel Design (6th Edition)EngineeringISBN:9780134589657Author:Jack C. McCormac, Stephen F. CsernakPublisher:PEARSON Fundamentals of Materials Science and Engineering...EngineeringISBN:9781119175483Author:William D. Callister Jr., David G. RethwischPublisher:WILEY
Fundamentals of Materials Science and Engineering...EngineeringISBN:9781119175483Author:William D. Callister Jr., David G. RethwischPublisher:WILEY





