Bundle: Mechanics Of Materials, Loose-leaf Version, 9th + Mindtap Engineering, 1 Term (6 Months) Printed Access Card
9th Edition
ISBN: 9781337594318
Author: Barry J. Goodno; James M. Gere
Publisher: Cengage Learning
expand_more
expand_more
format_list_bulleted
Concept explainers
Videos
Textbook Question
Chapter 6, Problem 6.3.12P
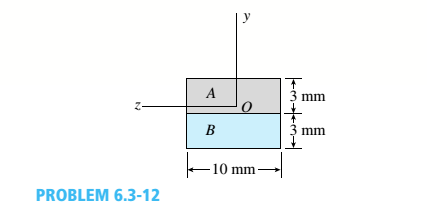
The cross section of a bimetallic strip is shown in the figure. Assuming that the moduli of elasticity for metals A and B are EA=168 GPa and EB= 90 GPa, respectively, determine the smaller of the two section moduli for the beam. (Recall that section modulus is equal to bending moment divided by maximum bending stress.) In which material does the maximum stress occur?
Expert Solution & Answer
Trending nowThis is a popular solution!
Students have asked these similar questions
14- effect of different carburizing treatments on the microstructure and mechanical
properties of a case produced by carburizing.
5-surface film between two surfaces is one of the main factors affecting wear.
2. Consider a polymeric membrane within a 6 cm diameter stirred ultrafiltration cell. The membrane is
30 μm thick. The membrane has pores equivalent in size to a spherical molecule with a molecular weight
of 100,000, a porosity of 80%, and a tortuosity of 2.5. On the feed side of the membrane, we have a
solution containing a protein at a concentration of 8 g L-1 with these properties: a = 3 nm and DAB = 6.0 ×
10-7 cm² s¹. The solution viscosity is 1 cP. The hydrodynamic pressure on the protein side of the
membrane is 20 pounds per square inch (psi) higher than on the filtrate side of the membrane. Assume
that the hydrodynamic pressure difference is much larger than the osmotic pressure difference
(advection >> diffusion). Determine the convective flow rate of the solution across the membrane.
1. Calculate the filtration flow rate (cm³ s¹) of a pure fluid across a 100 cm² membrane. Assume the
viscosity (µ) of the fluid is 1.8 cP. The porosity of the membrane is 40% and the thickness of the
membrane is 500 μm. The pores run straight through the membrane and these pores have a radius of
0.225 μm. The pressure drop applied across the membrane is 75 psi. (Note: 1 cP = 0.001 N s m²² = 0.001
Pa s.)
Chapter 6 Solutions
Bundle: Mechanics Of Materials, Loose-leaf Version, 9th + Mindtap Engineering, 1 Term (6 Months) Printed Access Card
Ch. 6 - A composite beam is constructed using a steel...Ch. 6 - A wood beam is strengthened using two steel plates...Ch. 6 - A composite beam consisting of fiberglass faces...Ch. 6 - A wood beam with cross-sectional dimensions 200 mm...Ch. 6 - A hollow box beam is constructed with webs of...Ch. 6 - A r o lukI f/frm f «m t ub e of ou t sid e d ia...Ch. 6 - A beam with a guided support and 10-ft span...Ch. 6 - A plastic-lined steel pipe has the cross-sectional...Ch. 6 - The cross section of a sand wie h beam consisting...Ch. 6 - The cross section of a sandwich beam consisting of...
Ch. 6 - A bimetallic beam used in a temperature-control...Ch. 6 - A simply supported composite beam 3 m long carries...Ch. 6 - A simply supported wooden I-beam with a 12-ft span...Ch. 6 - -14 A simply supported composite beam with a 3.6 m...Ch. 6 - -15 A composite beam is constructed froma wood...Ch. 6 - A wood beam in a historic theater is reinforced...Ch. 6 - Repeat Problem 6.2-1 but now assume that the steel...Ch. 6 - Repeat Problem 6.2-17 but now use a...Ch. 6 - A sandwich beam having steel faces enclosing a...Ch. 6 - A wood beam 8 in. wide and 12 in. deep (nominal...Ch. 6 - A simple beam of span length 3.2 m carries a...Ch. 6 - A simple beam that is 18 ft long supports a...Ch. 6 - The composite beam shown in the figure is simply...Ch. 6 - The cross section of a beam made of thin strips of...Ch. 6 - Consider the preceding problem if the beam has...Ch. 6 - A simple beam thai is IS ft long supports a...Ch. 6 - The cross section of a composite beam made of...Ch. 6 - A beam is constructed of two angle sections, each...Ch. 6 - The cross section of a bimetallic strip is shown...Ch. 6 - A W 12 x 50 steel wide-flange beam and a segment...Ch. 6 - A reinforced concrete beam (see figure) is acted...Ch. 6 - A reinforced concrete T-beam (see figure) is acted...Ch. 6 - A reinforced concrete slab (see figure) is...Ch. 6 - A wood beam reinforced using two channels is...Ch. 6 - A wood beam reinforced by an aluminum channel...Ch. 6 - A beam with a rectangular cross section supports...Ch. 6 - A wood beam with a rectangular cross section (see...Ch. 6 - Solve the preceding problem for the following...Ch. 6 - A simply supported wide-flange beam of span length...Ch. 6 - Solve the preceding problem using the fol...Ch. 6 - A wood cantilever beam with a rectangular cross...Ch. 6 - Solve the preceding problem for a cantilever beam...Ch. 6 - A 2-m-long cantilever beam is constructed using a...Ch. 6 - A wood beam AB with a rectangular cross section (4...Ch. 6 - A steel beam of I-section (see figure) is simply...Ch. 6 - A cantilever beam with a wide-flange cross section...Ch. 6 - Solve the preceding problem using a W 310 x 129...Ch. 6 - A cantilever beam of W 12 × 14 section and length...Ch. 6 - A cantilever beam built up from two channel...Ch. 6 - A built-Lip I-section steel beam with channels...Ch. 6 - Repeat Problem 6.4-14 but use the configuration of...Ch. 6 - A beam with a channel section is subjected to a...Ch. 6 - A beam with a channel section is subjected to a...Ch. 6 - An angle section with equal legs is subjected to a...Ch. 6 - An angle section with equal legs is subjected to a...Ch. 6 - A beam made up all woun equal leg angles is...Ch. 6 - The Z-section of Example D-7 is subjected to M = 5...Ch. 6 - The cross section of a steel beam is constructed...Ch. 6 - The cross section of a steel beam is shown in the...Ch. 6 - A beam with a semicircular cross section of radius...Ch. 6 - .10 A built-up bourn supporting a condominium...Ch. 6 - Asteelpost (E = 30 × 106 psi) having thickness t =...Ch. 6 - A C 200 x 17.1 channel section has an angle with...Ch. 6 - A cold-formed steel section is made by folding a...Ch. 6 - A simple beam with a W 10 x 30 wide-flange cross...Ch. 6 - Solve the preceding problem for a W 250 × 44.8...Ch. 6 - A beam of wide-flange shape, W 8 x 28, has the...Ch. 6 - Solve the preceding problem for a W 200 × 41,7...Ch. 6 - Calculate the distance e from the cent crime of...Ch. 6 - Calculate the distance e from the centerline of...Ch. 6 - The cross section of an unbalanced wide-flange...Ch. 6 - The cross section of an unbalanced wide-flange...Ch. 6 - The cross section of a channel beam with double...Ch. 6 - The cross section of a slit circular tube of...Ch. 6 - The cross section of a slit square tube of...Ch. 6 - The cross section of a slit rectangular tube of...Ch. 6 - A U-shaped cross section of constant thickness is...Ch. 6 - Derive the following formula for the distance e...Ch. 6 - Derive the following formula for the distance e...Ch. 6 - The cross section of a sign post of constant...Ch. 6 - A cross section in the shape of a circular arc of...Ch. 6 - Determine the shape factor f for a cross section...Ch. 6 - (a) Determine the shape factor/for a hollow...Ch. 6 - A propped cantilever beam of length L = 54 in....Ch. 6 - A steel beam of rectangular cross section is 40 mm...Ch. 6 - .5 Calculate the shape factor j for the...Ch. 6 - Solve the preceding problem for a wide-flange beam...Ch. 6 - Determine the plastic modulus Z and shape...Ch. 6 - Prob. 6.10.8PCh. 6 - Prob. 6.10.9PCh. 6 - Prob. 6.10.10PCh. 6 - A hollow box beam with height h = 16 in,, width h...Ch. 6 - Solve the preceding problem for a box beam with...Ch. 6 - A hollow box beam with height h = 9.5 in., inside...Ch. 6 - Solve the preceding problem for a box beam with...Ch. 6 - The hollow box beam shown in the figure is...Ch. 6 - Prob. 6.10.16PCh. 6 - Prob. 6.10.17PCh. 6 - A singly symmetric beam with a T-section (see...Ch. 6 - A wide-flange beam with an unbalanced cross...Ch. 6 - .20 Determine the plastic moment Mpfor beam having...
Knowledge Booster
Learn more about
Need a deep-dive on the concept behind this application? Look no further. Learn more about this topic, mechanical-engineering and related others by exploring similar questions and additional content below.Similar questions
- 3. Tong and Anderson (1996) obtained for BSA the following data in a polyacrylamide gel for the partition coefficient (K) as a function of the gel volume fraction (4). The BSA they used had a molecular weight of 67,000, a molecular radius of 3.6 nm, and a diffusivity of 6 × 10-7 cm2 s-1. Compare the Ogston equation K=exp + to their data and obtain an estimate for the radius of the cylindrical fibers (af) that comprise the gel. Hint: You will need to plot Ink as a function of gel volume fraction as part of your analysis. Please include your MATLAB, or other, code with your solution. Gel Volume Fraction (4) KBSA 0.00 1.0 0.025 0.35 0.05 0.09 0.06 0.05 0.075 0.017 0.085 0.02 0.105 0.03arrow_forwardAssignment 10, Question 1, Problem Book #189 Problem Statement An ideal Brayton cycle operates with no reheat, intercooling, or regeneration. The com- pressor inlet conditions are 30°C and 1 bar. The compression ratio is 11. The turbine inlet temperature is 1,300 K. Determine the turbine exit temperature, the thermal efficiency, and the back work ratio. Use an air standard analysis. Answer Table Correct Stage Description Your Answer Answer * 1 Compressor inlet enthalpy (kJ/kg) Due Date Grade (%) Weight Attempt Action/Message Part Type 1 2 1 Compressor inlet relative pressure 1 Compressor exit relative pressure 1 Compressor exit enthalpy (kJ/kg) Compressor work (kJ/kg) Turbine inlet enthalpy (kJ/kg) Dec 5, 2024 11:59 pm Dec 5, 2024 11:59 pm Dec 5, 2024 11:59 pm 0.0 0.0 1 1/5 Submit Stage 1 0.0 1 1 Dec 5, 2024 11:59 pm 0.0 1 Dec 5, 2024 11:59 pm 0.0 1 2 Turbine inlet relative pressure Dec 5, 2024 11:59 pm Dec 5, 2024 11:59 pm 0.0 1 1/5 0.0 1 2 Combustion chamber heat addition (kJ/kg) Dec…arrow_forwardAssignment 10, Question 4, Problem Book #202 Problem Statement An ideal Brayton cycle with a two-stage compressor, a two-stage turbine, and a regenerator operates with a mass flow rate of 25 kg/s. The regenerator cold inlet is at 490 K and its effectiveness is 60%. Ambient conditions are 90 kPa and 20°C. The intercooler operates at 450 kPa and the reheater operates at 550 kPa. The temperature at the exit of the combustion chamber is 1,400 K. Heat is removed in the intercooler at a rate of 2.5 MW and heat is added in the reheater at a rate of 10 MW. Determine the thermal efficiency and the back work ratio. Use a cold air standard analysis with cp = 1.005 kJ/(kg K) and k = 1.4. . Answer Table Stage Description Your Answer Correct Answer Due Date Grade (%) 1 Thermal efficiency (%) Dec 5, 2024 11:59 pm 0.0 1 Weight Attempt Action/Message 1/5 Part Type Submit 1 Back work ratio (%) Dec 5, 2024 11:59 pm 0.0 1 * Correct answers will only show after due date has passed.arrow_forward
- Assignment 10, Question 3, Problem Book #198 Problem Statement Consider a Brayton cycle with a regenerator. The regenerator has an effectiveness of 75%. The compressor inlet conditions are 1.2 bar and 300 K and the mass flowrate is 4.5 kg/s. The compressor outlet pressure is 9 bar. Both the compressor and turbine consist of a single isentropic stage. What minimum power output must be achieved before the regenerator begins to have a benefit? Use an air-standard analysis. Answer Table Correct Answer Stage Description Your Answer Due Date Grade (%) Part Weight Attempt Action/Message Туре 1 Power output (MW) Dec 5, 2024 11:59 pm 0.0 1 1/5 Submit * Correct answers will only show after due date has passed.arrow_forwardQ-3 Consider an engine operating on the ideal Diesel cycle with air as the working fluid. The volume of the cylinder is 1200 cm³ at the beginning of the Compression process, 75 cm³ at the end, and 150 cm³ after the heat addition process. Air is at 17°c and lookpa at the beginning of the compression proc ess. Determine @ The pressure at the beginning of the heat rejection process. the net work per cycle in kjⒸthe mean effective pressur. Answers @264.3 KN/m² ②0.784 kj or 544-6 kj © 697 KN 19 2 marrow_forwardIn the system shown in the (img 1), water flows through the pump at a rate of 50L/s. The permissible NPSH providedby the manufacturer with that flow is 3.6 m. Determine the maximum height Delta z above the water surface at which the Pump can be installed to operate without cavitation. Include all losses in the suction tube. What is the value of the smaller total losses? What is the value of minor-minor losses? What is the value of major-minor losses?arrow_forward
- A plastic canister whose bottom surface can be approximated as a flat surface1.9 m and 3 m long, travels through the water at 19 °C with a speed of up to 48 km/h. Determine: Drag due to friction that water exerts on the boat The power needed to overcome itarrow_forward(Fig. 1) shows the performance of a centrifugal pump for various diameters of theimpeller. For such a pump with a 5" diameter impeller, what power, in hp, would be expected to supply 5 L/s?what is its efficiency, in %?A pumping system requires 6 L/s of water with a load of 8 m, which of the pumpsof (fig. 1) would you recommend for this application?;arrow_forwardYou have the following information about a ship (image 1) Determine:a) Calculation of the block coefficient. b) Calculation of the wake coefficient. c) Determine the length of the wake.arrow_forward
- A stainless steel canoe moves horizontally along the surface of a lake at 3.7 mi/h. TheThe lake's water temperature is 60°F. The bottom of the canoe is 25 ft long and flat. The boundary layer inThe bottom of the canoe is laminar or turbulent. the value of kinematic viscosity is? the value of the Reynolds number is?arrow_forwardExample Example 1 A vertical tubular test section is to be installed in an experimental high pressure water loop. The tube is 10.16 mm i.d. and 3.66 m long heated uniformly over its EXAMPLE 73 length. An estimate of the pressure drop across the test section is required as a function of the flow-rate of water entering the test section at 204°C and 68.9 bar. (1) Calculate the pressure drop over the test section for a water flow of 0.108 kg/s with a power of 100 kW applied to the tube using (i) the homogeneous model (ii) the Martinelli-Nelson model (iii) The Thom correlation (iv) the Baroczy correlation (2) Estimate the pressure drop versus flow-rate relationship over the range 0.108 to 0.811 kg/s (2-15 USGPM) for a power of 100 kW and 200 kW applied to the tube using (i) the Martinelli-Nelson model (ii) the Baroczy correlationarrow_forward"A seismograph detects vibrations caused by seismic movements. To model this system, it is assumed that the structure undergoes a vibration with a known amplitude band frequency w (rad/s), such that its vertical displacement is given by xB=bsin(wt). This movement of the structure will produce a relative acceleration in the mass m of 2 kg, whose displacement 2 will be plotted on a roller." x= 15 kN/m Structure -WI 24 mm (Ctrl) sin(wt) b(w/w)² √√1 (w/w)] + [25(w/w)]²' "The seismograph's roller measures 60 mm, and a maximum vibration amplitude of the structure of b<5 mm is expected. Design the damper (constant c) to ensure that, for a constant oscillation, the seismograph functions correctly and the needle does not move off the roller."arrow_forward
arrow_back_ios
SEE MORE QUESTIONS
arrow_forward_ios
Recommended textbooks for you
Mechanics of Materials (MindTap Course List)Mechanical EngineeringISBN:9781337093347Author:Barry J. Goodno, James M. GerePublisher:Cengage Learning
Mechanics of Materials (MindTap Course List)
Mechanical Engineering
ISBN:9781337093347
Author:Barry J. Goodno, James M. Gere
Publisher:Cengage Learning
Everything About COMBINED LOADING in 10 Minutes! Mechanics of Materials; Author: Less Boring Lectures;https://www.youtube.com/watch?v=N-PlI900hSg;License: Standard youtube license