
A First Course in Probability (10th Edition)
10th Edition
ISBN: 9780134753119
Author: Sheldon Ross
Publisher: PEARSON
expand_more
expand_more
format_list_bulleted
Concept explainers
Textbook Question
Chapter 6, Problem 6.18STPE
6.18. Let
4V’H and
Y, be independent random
= i1.. . ., .X’,, = i,1} = P{)1 = i1.. . .. = i,1}
1
= ,ij=o,1, j=1ij=:1I.
(n
\
N = 1=1Ix—)’;
I denote the number of coordinates at which the two vectors have different values. Also, let
M denote the number of values of i for which
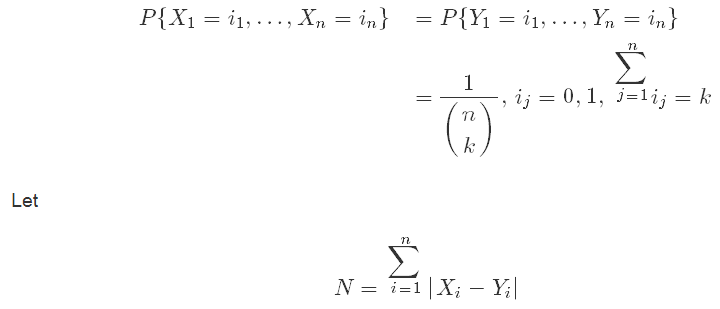
= 0.
a. Relate N to M.
b. What is the distribution of M?
c. Find E [ N].
d. Find Var (N).
Expert Solution & Answer
Want to see the full answer?
Check out a sample textbook solution
Students have asked these similar questions
The same final exam of the astronomy course was given to two groups of students. The maximum number of points that a student can score is 100. The first group consisted of a random sample of 10 students who were taught by Professor A. Students from the first group obtained the following results:
87 88 91 88 86 92 81 93 73 99
The second group consisted of a random sample of 9 students who were taught by Professor B. Students from the second group obtained the following results:
74 74 79 97 67 88 86 83 78
Compute the mean squares of between-group variability, MSBET. Round your answer to two decimal places.
1. Consider the following preference ballots:
Number of voters
Rankings 6 5 4 2
1st choice A DCB
DC
2nd choice B B D
3rd choice DCBD
4th choice CA
AAA
For each of the four voting systems we have studied, determine who would win the election
in each case. (Remember: For plurality with runoff, all but the top two vote-getters are
simultaneously eliminated at the end of round 1.)
dangers of college kids carrying concealed handguns
Chapter 6 Solutions
A First Course in Probability (10th Edition)
Ch. 6 - Two fair dice are rolled. Find the joint...Ch. 6 - Suppose that 3 balls are chosen without...Ch. 6 - In Problem 8 t, suppose that the white balls are...Ch. 6 - Repeat Problem 6.2 when the ball selected is...Ch. 6 - Repeat Problem 6.3a when the ball selected is...Ch. 6 - The severity of a certain cancer is designated by...Ch. 6 - Consider a sequence of independent Bernoulli...Ch. 6 - Prob. 6.8PCh. 6 - The joint probability density function of X and Y...Ch. 6 - Prob. 6.10P
Ch. 6 - In Example Id, verify that f(x,y)=2exe2y,0x,0y, is...Ch. 6 - The number of people who enter a drugstore in a...Ch. 6 - A man and a woman agree to meet at a certain...Ch. 6 - An ambulance travels back and forth at a constant...Ch. 6 - The random vector (X,Y) is said to be uniformly...Ch. 6 - Suppose that n points are independently chosen at...Ch. 6 - Prob. 6.17PCh. 6 - Let X1 and X2 be independent binomial random...Ch. 6 - Show that f(x,y)=1x, 0yx1 is a joint density...Ch. 6 - Prob. 6.20PCh. 6 - Let f(x,y)=24xy0x1,0y1,0x+y1 and let it equal 0...Ch. 6 - The joint density function of X and Y is...Ch. 6 - Prob. 6.23PCh. 6 - Consider independent trials, each of which results...Ch. 6 - Suppose that 106 people arrive at a service...Ch. 6 - Prob. 6.26PCh. 6 - Prob. 6.27PCh. 6 - The time that it takes to service a car is an...Ch. 6 - The gross daily sales at a certain restaurant are...Ch. 6 - Jills bowling scores are approximately normally...Ch. 6 - According to the U.S. National Center for Health...Ch. 6 - Monthly sales are independent normal random...Ch. 6 - Let X1 and X2 be independent normal random...Ch. 6 - Prob. 6.34PCh. 6 - Teams 1, 2, 3, 4 are all scheduled to play each of...Ch. 6 - Let X1,...,X10 be independent with the same...Ch. 6 - The expected number of typographical errors on a...Ch. 6 - The monthly worldwide average number of airplane...Ch. 6 - In Problem 6.4, calculate the conditional...Ch. 6 - In Problem 6.3 calculate the conditional...Ch. 6 - Prob. 6.41PCh. 6 - Prob. 6.42PCh. 6 - Prob. 6.43PCh. 6 - The joint probability mass function of X and Y is...Ch. 6 - Prob. 6.45PCh. 6 - Prob. 6.46PCh. 6 - An insurance company supposes that each person has...Ch. 6 - If X1,X2,X3 are independent random variables that...Ch. 6 - Prob. 6.49PCh. 6 - If 3 trucks break down at points randomly...Ch. 6 - Consider a sample of size 5 from a uniform...Ch. 6 - Prob. 6.52PCh. 6 - Let X(1),X(2),...,X(n) be the order statistics of...Ch. 6 - Let Z1 and Z2 be independent standard normal...Ch. 6 - Derive the distribution of the range of a sample...Ch. 6 - Let X and Y denote the coordinates of a point...Ch. 6 - Prob. 6.57PCh. 6 - Prob. 6.58PCh. 6 - Prob. 6.59PCh. 6 - Prob. 6.60PCh. 6 - Repeat Problem 6.60 when X and Y are independent...Ch. 6 - Prob. 6.62PCh. 6 - Prob. 6.63PCh. 6 - In Example 8b, let Yk+1=n+1i=1kYi. Show that...Ch. 6 - Consider an urn containing n balls numbered 1.. .....Ch. 6 - Suppose X,Y have a joint distribution function...Ch. 6 - Prob. 6.2TECh. 6 - Prob. 6.3TECh. 6 - Solve Buffons needle problem when LD.Ch. 6 - If X and Y are independent continuous positive...Ch. 6 - Prob. 6.6TECh. 6 - Prob. 6.7TECh. 6 - Let X and Y be independent continuous random...Ch. 6 - Let X1,...,Xn be independent exponential random...Ch. 6 - The lifetimes of batteries are independent...Ch. 6 - Prob. 6.11TECh. 6 - Show that the jointly continuous (discrete) random...Ch. 6 - In Example 5e t, we computed the conditional...Ch. 6 - Suppose that X and Y are independent geometric...Ch. 6 - Consider a sequence of independent trials, with...Ch. 6 - If X and Y are independent binomial random...Ch. 6 - Suppose that Xi,i=1,2,3 are independent Poisson...Ch. 6 - Prob. 6.18TECh. 6 - Let X1,X2,X3 be independent and identically...Ch. 6 - Prob. 6.20TECh. 6 - Suppose that W, the amount of moisture in the air...Ch. 6 - Let W be a gamma random variable with parameters...Ch. 6 - A rectangular array of mn numbers arranged in n...Ch. 6 - If X is exponential with rate , find...Ch. 6 - Suppose thatF(x) is a cumulative distribution...Ch. 6 - Show that if n people are distributed at random...Ch. 6 - Suppose that X1,...,Xn are independent exponential...Ch. 6 - Establish Equation (6.2) by differentiating...Ch. 6 - Show that the median of a sample of size 2n+1 from...Ch. 6 - Prob. 6.30TECh. 6 - Compute the density of the range of a sample of...Ch. 6 - Let X(1)X(2)...X(n) be the ordered values of n...Ch. 6 - Let X1,...,Xn be a set of independent and...Ch. 6 - Let X1,....Xn, be independent and identically...Ch. 6 - Prob. 6.35TECh. 6 - Prob. 6.36TECh. 6 - Suppose that (X,Y) has a bivariate normal...Ch. 6 - Suppose that X has a beta distribution with...Ch. 6 - 6.39. Consider an experiment with n possible...Ch. 6 - Prob. 6.40TECh. 6 - Prob. 6.41TECh. 6 - Each throw of an unfair die lands on each of the...Ch. 6 - The joint probability mass function of the random...Ch. 6 - Prob. 6.3STPECh. 6 - Let r=r1+...+rk, where all ri are positive...Ch. 6 - Suppose that X, Y, and Z are independent random...Ch. 6 - Let X and Y be continuous random variables with...Ch. 6 - The joint density function of X and Y...Ch. 6 - Consider two components and three types of shocks....Ch. 6 - Consider a directory of classified advertisements...Ch. 6 - The random parts of the algorithm in Self-Test...Ch. 6 - Prob. 6.11STPECh. 6 - The accompanying dartboard is a square whose sides...Ch. 6 - A model proposed for NBA basketball supposes that...Ch. 6 - Let N be a geometric random variable with...Ch. 6 - Prob. 6.15STPECh. 6 - You and three other people are to place bids for...Ch. 6 - Find the probability that X1,X2,...,Xn is a...Ch. 6 - 6.18. Let 4VH and Y, be independent random...Ch. 6 - Let Z1,Z2.....Zn be independent standard normal...Ch. 6 - Let X1,X2,... be a sequence of independent and...Ch. 6 - Prove the identity P{Xs,Yt}=P{Xs}+P{Yt}+P{Xs,Yt}1...Ch. 6 - In Example 1c, find P(Xr=i,Ys=j) when ji.Ch. 6 - A Pareto random variable X with parameters a0,0...Ch. 6 - Prob. 6.24STPECh. 6 - Prob. 6.25STPECh. 6 - Let X1,...,Xn, be independent nonnegative integer...
Knowledge Booster
Learn more about
Need a deep-dive on the concept behind this application? Look no further. Learn more about this topic, probability and related others by exploring similar questions and additional content below.Similar questions
- iid B1 Suppose X1, ..., Xn fx(x), where 2 fx(x) = x exp(−x²/0), 0<< (0 otherwise). (a) Find the maximum likelihood estimator of 0. (b) Show that the MLE is an unbiased estimator of 0. (c) Find the MSE of the MLE. Hint: For parts (b) and (c), you may use integration by parts.arrow_forwardiid B1 Suppose X1, ..., Xn fx(x), where 2 fx(x) = x exp(−x²/0), 0<< (0 otherwise). (a) Find the maximum likelihood estimator of 0. (b) Show that the MLE is an unbiased estimator of 0. (c) Find the MSE of the MLE. Hint: For parts (b) and (c), you may use integration by parts.arrow_forward2) Suppose we select two values x and y independently from the uniform distribution on [0,1]. What is the probability that xyarrow_forward100 identical balls are rolling along a straight line. They all have speed equal to v, but some of them might move in opposite directions. When two of them collide they immediately switch their direction and keep the speed v. What is the maximum number of collisions that can happen? Let f(w) be a function of vector w Є RN, i.e. f(w) = 1+e Determine the first derivative and matrix of second derivatives off with respect to w. Let A Є RN*N be a symmetric, positive definite matrix and bЄ RN a vector. If x ER, evaluate the integral Z(A,b) = e¯xAx+bx dx as a function of A and b. John throws a fair die with faces labelled 1 to 6. ⚫ He gains 10 points if the die shows 1. ⚫ He gains 1 point if the die shows 2 or 4. • No points are allocated otherwise. Let X be the random variable describing John's gain at each throw. Determine the variance of X.arrow_forwardFemale Male Totals Less than High School Diploma 0.077 0.110 0.187 High School Diploma 0.154 0.201 0.355 Some College/University 0.141 0.129 0.270 College/University Graduate 0.092 0.096 0.188 Totals 0.464 0.536 1.000arrow_forwardFemale Male Totals Less than High School Diploma 0.077 0.110 0.187 High School Diploma 0.154 0.201 0.355 Some College/University 0.141 0.129 0.270 College/University Graduate 0.092 0.096 0.188 Totals 0.464 0.536 1.000arrow_forwardFemale Male Totals Less than High School Diploma 0.077 0.110 0.187 High School Diploma 0.154 0.201 0.355 Some College/University 0.141 0.129 0.270 College/University Graduate 0.092 0.096 0.188 Totals 0.464 0.536 1.000arrow_forwardFemale Male Totals Less than High School Diploma 0.077 0.110 0.187 High School Diploma 0.154 0.201 0.355 Some College/University 0.141 0.129 0.270 College/University Graduate 0.092 0.096 0.188 Totals 0.464 0.536 1.000arrow_forward6.54 Let Y₁, Y2,..., Y, be independent Poisson random variables with means 1, 2,..., An respectively. Find the a probability function of Y. b conditional probability function of Y₁, given that Y = m. Y₁ = m. c conditional probability function of Y₁+Y2, given that 6.55 Customers arrive at a department store checkout counter according to a Poisson distribution with a mean of 7 per hour. In a given two-hour period, what is the probability that 20 or more customers will arrive at the counter? 6.56 The length of time necessary to tune up a car is exponentially distributed with a mean of .5 hour. If two cars are waiting for a tune-up and the service times are independent, what is the probability that the total time for the two tune-ups will exceed 1.5 hours? [Hint: Recall the result of Example 6.12.] 6.57 Let Y, Y2,..., Y,, be independent random variables such that each Y, has a gamma distribution with parameters a, and B. That is, the distributions of the Y's might have different a's, but…arrow_forward6.82 6.83 6.84 6.85 *6.86 6.87 If Y is a continuous random variable and m is the median of the distribution, then m is such that P(Ym) = P(Y ≥ m) = 1/2. If Y₁, Y2,..., Y, are independent, exponentially dis- tributed random variables with mean ẞ and median m, Example 6.17 implies that Y(n) = max(Y₁, Y., Y) does not have an exponential distribution. Use the general form of FY() (y) to show that P(Y(n) > m) = 1 - (.5)". Refer to Exercise 6.82. If Y₁, Y2,..., Y,, is a random sample from any continuous distribution with mean m, what is P(Y(n) > m)? Refer to Exercise 6.26. The Weibull density function is given by -my" m-le-y/a f(y)= α 0. y > 0, elsewhere, where a and m are positive constants. If a random sample of size n is taken from a Weibull distributed population, find the distribution function and density function for Y(1) = min(Y1, Y2,Y). Does Y(1) = have a Weibull distribution? Let Y₁ and Y2 be independent and uniformly distributed over the interval (0, 1). Find P(2Y(1) 0, elsewhere,…arrow_forward6.26 The Weibull density function is given by e-y/a f(y) = α 0. y > 0, elsewhere, where a and m are positive constants. This density function is often used as a model for the lengths of life of physical systems. Suppose Y has the Weibull density just given. Find a the density function of UY". b E(Y) for any positive integer k. 6.27 Let Y have an exponential distribution with mean ẞ. 6.28 6.29 a Prove that W = √Y has a Weibull density with α = ẞ and m = 2. b Use the result in Exercise 6.26(b) to give E(Yk/2) for any positive integer k. Let Y have a uniform (0, 1) distribution. Show that U = -2ln(Y) has an exponential distri- bution with mean 2. The speed of a molecule in a uniform gas at equilibrium is a random variable V whose density function is given by 6.30 6.31 6.32 f(v) = av²e-by², v > 0, where b = m/2kT and k, T, and m denote Boltzmann's constant, the absolute temperature, and the mass of the molecule, respectively. a Derive the distribution of W = mV2/2, the kinetic energy of…arrow_forwardQIA Let F-4c24, countible or, A, countible), show that is o-algebra. B Let (Fne N) is family of a-algebra on 2, prove that F. o-algebra Q2: Prove that: 1. X, is martingale -esin 2. M, -e sin B,, is martingale by using Ito formula Q3: A Let X, has stochastic differential with drift p(x)=-bx + c, and diffusion o²(x)=4x, let Y√X,, where X, ≥0, find dr B: Let X, -(-s), Ito integral process, find dx, and [x.xko). Q4: Let Y, =[x,dB, is Ito integral, such that X, is nonrandom process, find: التوزيع 1. The distribution of Y 2. The moment generating function of Y,.arrow_forwardarrow_back_iosSEE MORE QUESTIONSarrow_forward_ios
Recommended textbooks for you
 Linear Algebra: A Modern IntroductionAlgebraISBN:9781285463247Author:David PoolePublisher:Cengage Learning
Linear Algebra: A Modern IntroductionAlgebraISBN:9781285463247Author:David PoolePublisher:Cengage Learning

Linear Algebra: A Modern Introduction
Algebra
ISBN:9781285463247
Author:David Poole
Publisher:Cengage Learning
Mod-01 Lec-01 Discrete probability distributions (Part 1); Author: nptelhrd;https://www.youtube.com/watch?v=6x1pL9Yov1k;License: Standard YouTube License, CC-BY
Discrete Probability Distributions; Author: Learn Something;https://www.youtube.com/watch?v=m9U4UelWLFs;License: Standard YouTube License, CC-BY
Probability Distribution Functions (PMF, PDF, CDF); Author: zedstatistics;https://www.youtube.com/watch?v=YXLVjCKVP7U;License: Standard YouTube License, CC-BY
Discrete Distributions: Binomial, Poisson and Hypergeometric | Statistics for Data Science; Author: Dr. Bharatendra Rai;https://www.youtube.com/watch?v=lHhyy4JMigg;License: Standard Youtube License