A First Course in Probability (10th Edition)
10th Edition
ISBN: 9780134753119
Author: Sheldon Ross
Publisher: PEARSON
expand_more
expand_more
format_list_bulleted
Videos
Textbook Question
Chapter 6, Problem 6.12STPE
The accompanying dartboard is a square whose sides are of length 6: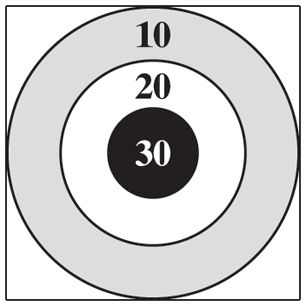 
The three circles are all centered at the center of the board and are of radii 1, 2, and 3, respectively. Darts landing within the circle of radius I score 30 points, those landing outside this circle, but within the circle of radius 2, are worth 20 points, and those landing outside the circle of radius 2, but within the circle of radius 3, are worth 10 points. Darts that do not land within the circle of radius 3 do not score any points. Assuming that each dart that you throw will, independently of what occurred on your previous throws, land on a point uniformly distributed in the square, find the probabilities of the accompanying
a. You score 20 on a throw of the dart.
b. You score at least 20 on a throw of the dart.
c. You score 0 on a throw of the dart.
d. The
e. Both of your first two throws score at least 10.
f. Your total score after two throws is 30.
Expert Solution & Answer
Want to see the full answer?
Check out a sample textbook solution
Students have asked these similar questions
Problem: The probability density function of a random variable is given by the exponential
distribution
Find the probability that
f(x) = {0.55e−0.55x 0 < x, O elsewhere}
a. the time to observe a particle is more than 200 microseconds.
b. the time to observe a particle is less than 10 microseconds.
Problem: The probability density function of a random variable is given by the exponential
distribution
Find the probability that
f(x) = {0.55e-0.55 x 0 < x, O elsewhere}
a. the time to observe a particle is more than 200 microseconds.
b. the time to observe a particle is less than 10 microseconds.
Unknown to a medical researcher, 7 out of 24 patients have a heart problem that will result in death if they receive the test drug. 5 patients are randomly selected to receive the drug and the rest receive a placebo. What is the probability that less than 4 patients will die? Express as a fraction or a decimal number rounded to four decimal places.
Chapter 6 Solutions
A First Course in Probability (10th Edition)
Ch. 6 - Two fair dice are rolled. Find the joint...Ch. 6 - Suppose that 3 balls are chosen without...Ch. 6 - In Problem 8 t, suppose that the white balls are...Ch. 6 - Repeat Problem 6.2 when the ball selected is...Ch. 6 - Repeat Problem 6.3a when the ball selected is...Ch. 6 - The severity of a certain cancer is designated by...Ch. 6 - Consider a sequence of independent Bernoulli...Ch. 6 - Prob. 6.8PCh. 6 - The joint probability density function of X and Y...Ch. 6 - Prob. 6.10P
Ch. 6 - In Example Id, verify that f(x,y)=2exe2y,0x,0y, is...Ch. 6 - The number of people who enter a drugstore in a...Ch. 6 - A man and a woman agree to meet at a certain...Ch. 6 - An ambulance travels back and forth at a constant...Ch. 6 - The random vector (X,Y) is said to be uniformly...Ch. 6 - Suppose that n points are independently chosen at...Ch. 6 - Prob. 6.17PCh. 6 - Let X1 and X2 be independent binomial random...Ch. 6 - Show that f(x,y)=1x, 0yx1 is a joint density...Ch. 6 - Prob. 6.20PCh. 6 - Let f(x,y)=24xy0x1,0y1,0x+y1 and let it equal 0...Ch. 6 - The joint density function of X and Y is...Ch. 6 - Prob. 6.23PCh. 6 - Consider independent trials, each of which results...Ch. 6 - Suppose that 106 people arrive at a service...Ch. 6 - Prob. 6.26PCh. 6 - Prob. 6.27PCh. 6 - The time that it takes to service a car is an...Ch. 6 - The gross daily sales at a certain restaurant are...Ch. 6 - Jills bowling scores are approximately normally...Ch. 6 - According to the U.S. National Center for Health...Ch. 6 - Monthly sales are independent normal random...Ch. 6 - Let X1 and X2 be independent normal random...Ch. 6 - Prob. 6.34PCh. 6 - Teams 1, 2, 3, 4 are all scheduled to play each of...Ch. 6 - Let X1,...,X10 be independent with the same...Ch. 6 - The expected number of typographical errors on a...Ch. 6 - The monthly worldwide average number of airplane...Ch. 6 - In Problem 6.4, calculate the conditional...Ch. 6 - In Problem 6.3 calculate the conditional...Ch. 6 - Prob. 6.41PCh. 6 - Prob. 6.42PCh. 6 - Prob. 6.43PCh. 6 - The joint probability mass function of X and Y is...Ch. 6 - Prob. 6.45PCh. 6 - Prob. 6.46PCh. 6 - An insurance company supposes that each person has...Ch. 6 - If X1,X2,X3 are independent random variables that...Ch. 6 - Prob. 6.49PCh. 6 - If 3 trucks break down at points randomly...Ch. 6 - Consider a sample of size 5 from a uniform...Ch. 6 - Prob. 6.52PCh. 6 - Let X(1),X(2),...,X(n) be the order statistics of...Ch. 6 - Let Z1 and Z2 be independent standard normal...Ch. 6 - Derive the distribution of the range of a sample...Ch. 6 - Let X and Y denote the coordinates of a point...Ch. 6 - Prob. 6.57PCh. 6 - Prob. 6.58PCh. 6 - Prob. 6.59PCh. 6 - Prob. 6.60PCh. 6 - Repeat Problem 6.60 when X and Y are independent...Ch. 6 - Prob. 6.62PCh. 6 - Prob. 6.63PCh. 6 - In Example 8b, let Yk+1=n+1i=1kYi. Show that...Ch. 6 - Consider an urn containing n balls numbered 1.. .....Ch. 6 - Suppose X,Y have a joint distribution function...Ch. 6 - Prob. 6.2TECh. 6 - Prob. 6.3TECh. 6 - Solve Buffons needle problem when LD.Ch. 6 - If X and Y are independent continuous positive...Ch. 6 - Prob. 6.6TECh. 6 - Prob. 6.7TECh. 6 - Let X and Y be independent continuous random...Ch. 6 - Let X1,...,Xn be independent exponential random...Ch. 6 - The lifetimes of batteries are independent...Ch. 6 - Prob. 6.11TECh. 6 - Show that the jointly continuous (discrete) random...Ch. 6 - In Example 5e t, we computed the conditional...Ch. 6 - Suppose that X and Y are independent geometric...Ch. 6 - Consider a sequence of independent trials, with...Ch. 6 - If X and Y are independent binomial random...Ch. 6 - Suppose that Xi,i=1,2,3 are independent Poisson...Ch. 6 - Prob. 6.18TECh. 6 - Let X1,X2,X3 be independent and identically...Ch. 6 - Prob. 6.20TECh. 6 - Suppose that W, the amount of moisture in the air...Ch. 6 - Let W be a gamma random variable with parameters...Ch. 6 - A rectangular array of mn numbers arranged in n...Ch. 6 - If X is exponential with rate , find...Ch. 6 - Suppose thatF(x) is a cumulative distribution...Ch. 6 - Show that if n people are distributed at random...Ch. 6 - Suppose that X1,...,Xn are independent exponential...Ch. 6 - Establish Equation (6.2) by differentiating...Ch. 6 - Show that the median of a sample of size 2n+1 from...Ch. 6 - Prob. 6.30TECh. 6 - Compute the density of the range of a sample of...Ch. 6 - Let X(1)X(2)...X(n) be the ordered values of n...Ch. 6 - Let X1,...,Xn be a set of independent and...Ch. 6 - Let X1,....Xn, be independent and identically...Ch. 6 - Prob. 6.35TECh. 6 - Prob. 6.36TECh. 6 - Suppose that (X,Y) has a bivariate normal...Ch. 6 - Suppose that X has a beta distribution with...Ch. 6 - 6.39. Consider an experiment with n possible...Ch. 6 - Prob. 6.40TECh. 6 - Prob. 6.41TECh. 6 - Each throw of an unfair die lands on each of the...Ch. 6 - The joint probability mass function of the random...Ch. 6 - Prob. 6.3STPECh. 6 - Let r=r1+...+rk, where all ri are positive...Ch. 6 - Suppose that X, Y, and Z are independent random...Ch. 6 - Let X and Y be continuous random variables with...Ch. 6 - The joint density function of X and Y...Ch. 6 - Consider two components and three types of shocks....Ch. 6 - Consider a directory of classified advertisements...Ch. 6 - The random parts of the algorithm in Self-Test...Ch. 6 - Prob. 6.11STPECh. 6 - The accompanying dartboard is a square whose sides...Ch. 6 - A model proposed for NBA basketball supposes that...Ch. 6 - Let N be a geometric random variable with...Ch. 6 - Prob. 6.15STPECh. 6 - You and three other people are to place bids for...Ch. 6 - Find the probability that X1,X2,...,Xn is a...Ch. 6 - 6.18. Let 4VH and Y, be independent random...Ch. 6 - Let Z1,Z2.....Zn be independent standard normal...Ch. 6 - Let X1,X2,... be a sequence of independent and...Ch. 6 - Prove the identity P{Xs,Yt}=P{Xs}+P{Yt}+P{Xs,Yt}1...Ch. 6 - In Example 1c, find P(Xr=i,Ys=j) when ji.Ch. 6 - A Pareto random variable X with parameters a0,0...Ch. 6 - Prob. 6.24STPECh. 6 - Prob. 6.25STPECh. 6 - Let X1,...,Xn, be independent nonnegative integer...
Knowledge Booster
Learn more about
Need a deep-dive on the concept behind this application? Look no further. Learn more about this topic, probability and related others by exploring similar questions and additional content below.Similar questions
- Was wanting to check if my calculations were correct Suppose 52% of the population has a college degree. If a random sample of size 808 is selected, what is the probability that the proportion of persons with a college degree will be less than 54%? Round to four decimal places. after following the formula I got 0.8724arrow_forwardAt the beginning of each semester, students at the University of Minnesota receive one prepaid copy card that allows them to print from the copiers and printers on campus. The amount of money remaining on the card can be modeled by a linear equation where A represents how much remains on the card (in dollars) and p represents the number of pages that the student has printed. The graph of this linear equation is given below. 100 90 80 70 60 50 40 30 20 10 0 A = Amount on Card ($) 0 200 400 600 800 1000 1200 1400 1600 p = Number of Pages Printed What information does the vertical intercept tell you (represent) for this problem? Be sure to include specific details in your answer -- your answer should have both quantitative and qualitative data to describe the answer in terms of the question.arrow_forwardData management no 2 thanksarrow_forward
- G12 Data Management please help on the first question no 1 belowarrow_forwardTotal marks 14 4. Let X and Y be random variables on a probability space (N, F, P) that take values in [0, ∞). Assume that the joint density function of X and Y on [0, ∞) × [0, ∞) is given by f(x, y) = 2e-2x-y Find the probability P(0 ≤ X ≤ 1,0 ≤ y ≤ 2). (ii) spectively. [6 Marks] Find the the probability density function of X and Y, re- [5 Marks] 111) Are the X and Y independent? Justify your answer! [3 Marks]arrow_forwardTotal marks 17 4. Let (,,P) be a probability space and let X : → R be a ran- dom variable that has Gamma(2, 1) distribution, i.e., the distribution of the random variable X is the probability measure on ((0, ∞), B((0, ∞))) given by (i) dPx(x) = xex dx. Find the characteristic function of the random variable X. [8 Marks] (ii) Using the result of (i), calculate the first three moments of the random variable X, i.e., E(X") for n = 1, 2, 3. Using Markov's inequality involving E(X³), (iii) probability P(X > 10). [6 Marks] estimate the [3 Marks]arrow_forward
- 1. There are 8 balls in an urn, of which 6 balls are red, 1 ball is blue and 1 ball is white. You draw a ball from the urn at random, note its colour, do not return the ball to the urn, and then draw a second ball, note its colour, do not return the ball to the urn, and finally draw a third ball, note its colour. (i) (Q, F, P). Describe the corresponding discrete probability space [7 Marks] (ii) Consider the following event, A: At least one of the first two balls is red.arrow_forward3. Consider the following discrete probability space. Let = {aaa, bbb, ccc, abc, acb, bac, bca, cab, cba}, i.e., consists of 3-letter 'words' aaa, bbb, ccc, and all six possible 3-letter 'words' that have a single letter a, a single letter b, and a single letter c. The probability measure P is given by 1 P(w) = for each weΩ. 9 Consider the following events: A: the first letter of a 'word' is a, B: the second letter of a 'word' is a, C: the third letter of a 'word' is a. answer! Decide whether the statements bellow are true or false. Justify your (i) The events A, B, C are pairwise independent. (ii) The events A, B, C are independent. Total marks 7 [7 Marks]arrow_forwardLet X and Y have the following joint probability density function: fxy(x,y) =1/(x²²), for >>1, y>1 0, otherwise Let U = 5XY and V = 3 x. In all question parts below, give your answers to three decimal places (where appropriate). (a) The non-zero part of the joint probability density function of U and V is given by fu,v(u,v) = A√³uc for some constants A, B, C. Find the value of A. Answer: 5 Question 5 Answer saved Flag question Find the value of B. Answer: -1 Question 6 Answer saved P Flag question (b) The support of (U,V), namely the values of u and vthat correspond to the non-zero part of fu,v(u,v) given in part (a), is given by:arrow_forward
- Total marks 13. 3. There are three urns. Urn I contains 3 blue balls and 5 white balls; urn II contains 2 blue balls and 6 white balls; urn III contains 4 blue balls and 4 white balls. Rolling a dice, if 1 appears, we draw a ball from urn I; if 4 or 5 or 6 appears, we draw a ball from urn II; if 2, or 3 appears, we draw a ball from urn III. (i) What is the probability to draw a blue ball? [7 Marks] (ii) Assume that a blue ball is drawn. What is the probability that it came from Urn I? [6 Marks] Turn over. MA-252: Page 3 of 4arrow_forward3. Consider the discrete probability space with the sample space = {a, b, c, d, e, f, g, h} and the probability measure P given by P(w) for each wEN. Consider the following events: A = {a, c, e, g}, B = {b, c, d, e}, C = = {a, b, d, g}. Decide whether the statements bellow are true or false. Justify your answer! (i) The events A, B, C are pairwise independent. (ii) The events A, B, C are independent. Total marks 6 [6 Marks]arrow_forward2. space Consider the discrete probability space (N, F, P) with the sample N = {W1 W2 W3 W4 W5, W6, W7, W8, W9, W10, W11, W12}, is the power of 2, and the probability measure P is given by 1 P(wi) for each i = 1, 12. 12 Consider the following events: A = {W1, W3, W5, W7, W9, W11}, C = B = {W1, WA, W7, W8, W9, W12}, = {W3, WA, W5, W6, W9, W12}. Decide whether the statements bellow are true or false. Justify your answer! (i) The events A, B, C are pairwise independent. [5 Marks] Total marks 8 (ii) The events A, B, C are independent. [3 Marks]arrow_forward
arrow_back_ios
SEE MORE QUESTIONS
arrow_forward_ios
Recommended textbooks for you
Elementary Geometry For College Students, 7eGeometryISBN:9781337614085Author:Alexander, Daniel C.; Koeberlein, Geralyn M.Publisher:Cengage,
Trigonometry (MindTap Course List)TrigonometryISBN:9781305652224Author:Charles P. McKeague, Mark D. TurnerPublisher:Cengage Learning
Holt Mcdougal Larson Pre-algebra: Student Edition...AlgebraISBN:9780547587776Author:HOLT MCDOUGALPublisher:HOLT MCDOUGAL
Mathematics For Machine TechnologyAdvanced MathISBN:9781337798310Author:Peterson, John.Publisher:Cengage Learning,
Algebra: Structure And Method, Book 1AlgebraISBN:9780395977224Author:Richard G. Brown, Mary P. Dolciani, Robert H. Sorgenfrey, William L. ColePublisher:McDougal Littell
Elementary AlgebraAlgebraISBN:9780998625713Author:Lynn Marecek, MaryAnne Anthony-SmithPublisher:OpenStax - Rice University
Elementary Geometry For College Students, 7e
Geometry
ISBN:9781337614085
Author:Alexander, Daniel C.; Koeberlein, Geralyn M.
Publisher:Cengage,
Trigonometry (MindTap Course List)
Trigonometry
ISBN:9781305652224
Author:Charles P. McKeague, Mark D. Turner
Publisher:Cengage Learning
Holt Mcdougal Larson Pre-algebra: Student Edition...
Algebra
ISBN:9780547587776
Author:HOLT MCDOUGAL
Publisher:HOLT MCDOUGAL
Mathematics For Machine Technology
Advanced Math
ISBN:9781337798310
Author:Peterson, John.
Publisher:Cengage Learning,
Algebra: Structure And Method, Book 1
Algebra
ISBN:9780395977224
Author:Richard G. Brown, Mary P. Dolciani, Robert H. Sorgenfrey, William L. Cole
Publisher:McDougal Littell
Elementary Algebra
Algebra
ISBN:9780998625713
Author:Lynn Marecek, MaryAnne Anthony-Smith
Publisher:OpenStax - Rice University
Quadrilaterals: Missing Angles and Sides; Author: rhornfeck;https://www.youtube.com/watch?v=knVj1O0L2TM;License: Standard YouTube License, CC-BY
STD IX | State Board | Types of Quadrilateral; Author: Robomate;https://www.youtube.com/watch?v=wh0KQ4UB0EU;License: Standard YouTube License, CC-BY