
A piston–cylinder device initially contains 1.2 kg of air at 700 kPa and 200°C. At this state, the piston is touching on a pair of stops. The mass of the piston is such that 600-kPa pressure is required to move it. A valve at the bottom of the tank is opened, and air is withdrawn from the cylinder. The valve is closed when the volume of the cylinder decreases to 80 percent of the initial volume. If it is estimated that 40 kJ of heat is lost from the cylinder, determine (a) the final temperature of the air in the cylinder, (b) the amount of mass that has escaped from the cylinder, and (c) the work done. Use constant specific heats at the average temperature.
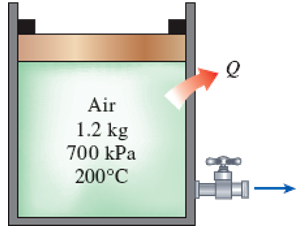
FIGURE P5–183
(a)
The final temperature of air in the cylinder.
Answer to Problem 183RP
The final temperature of air in the cylinder is
Explanation of Solution
Write the equation of mass balance.
Here, the inlet mass is
The change in mass of the system for the control volume is expressed as,
Here, the suffixes 1 and 2 indicates the initial and final states of the system.
Consider the piston-cylinder as the control volume. Initially the cylinder is filled with air and the valve is in closed position, further no other mass is allowed to enter the cylinder. Hence, the inlet mass is neglected i.e.
Rewrite the Equation (I) as follows.
Write the formula for initial volume of air present in the cylinder.
Here, the mass of air is
Write the formula for mass of air present in the cylinder at final state.
Here, the subscript 2 indicates the final state.
Write the energy balance equation.
Here, the heat transfer is
The pressure of
The Equation (V) reduced as follows.
Write the formula for boundary work done on the cylinder.
Here, the pressure required to move the piston is
The enthalpy and internal energy in terms of temperature and specific heats are expressed as follows.
Rewrite the Equation (VI) as follows.
The temperature of the air while exiting the cylinder is considered as the average temperature of initial and final temperatures.
Refer Table A-1, “Molar mass, gas constant, and critical-point properties”.
The gas constant
Refer Table A-2b, “Ideal-gas specific heats of various common gases”.
The specific heat at constant pressure
Conclusion:
Substitute
It is given that the final volume is 80 % of initial volume.
Substitute
Substitute
Substitute
Substitute
Use Engineering Equation Solver (EES) or online calculator to solve the Equation (X) and obtain the value of
Thus, the final temperature of air in the cylinder is
(b)
The amount of mass escaped from the cylinder.
Answer to Problem 183RP
The amount of mass escaped from the cylinder is
Explanation of Solution
The amount of mass escaped from the cylinder is nothing but the mass of air vented out until final state i.e.
Refer Equation (II) and (IX).
Conclusion:
Substitute
Thus, the amount of mass escaped from the cylinder is
(c)
The work done.
Answer to Problem 183RP
The amount of mass escaped from the cylinder is
Explanation of Solution
The work done is nothing but the work done on the piston to move it i.e. boundary work
Refer part (a).
Thus, the work done is
Want to see more full solutions like this?
Chapter 5 Solutions
THERMODYNAMICS (LL)-W/ACCESS >CUSTOM<
- A ship has 300 tonne of cargo in the hold, 24 m forward ofmidships. The displacement of the vessel is 6000 tonne and its centre of gravity is 1.2 m forward of midships.Find the new position of the centre of gravity if this cargo ismoved to an after hold, 40 m from midshipsarrow_forwardSketch and describe how ships are supported in dry dock. When and where does the greatest amount of stresses occur?arrow_forwardSketch and desribe a balanced rudder and how it is suspendedarrow_forward
- A ship 140 m long and 18 m beam floats at a draught of9 m. The immersed cross-sectionai areas at equai intervais are 5,60, 116, 145, 152, 153, 153, 151, 142, 85 and 0 m2 respectively.Calculate:(a) displacement(b) block coefficient(c) midship section area coefficient(d) prismatic coefficient.arrow_forwardA steamer has waterplane area 1680m2 recorded in water with relative denisty 1.013. Displacement = 1200 t, calculate difference in draught in salwater reltive denisity 1.025.arrow_forwardrelative velocity 11.72 m/s is correct, need help finding the angle pleasearrow_forward
- Determine the distance between the two automobiles 2 s after A has passed through the intersection.arrow_forwardA box barge 65 m long and 12 m wide floats at a draught of5.5 m in sea water. Calculate:(a) the displacement of the barge,(b) its draught in fresh waterarrow_forwardwhat is the angle of the velocity of block B? velocity is 7.46 in/s Determine the acceleration and angle of block B. (Round the acceleration value to three decimal places.)arrow_forward
- Determine the relative velocity of B with respect to A.arrow_forwardGenerate the kinematic diagram of the following mechanism. Then, draw their graphs and calculate their degrees of freedom (DoF) using Gruebler's formula.arrow_forwardAn elastic bar of length L = 1m and cross section A = 1cm2 spins with angular velocity ω about an axis, as shown in the figure below. The radial acceleration at a generic point x along the bar is a(x) = ω2x, where ω= 100rad/s is the angular velocity. The bar is pinned on the rotation axis at x = 0. A mass M = 1kg is attached to the right end of the bar. Due to the radial acceleration, the bar stretches along x with displacement function u(x). The displacement u(x) solves the BVP (strong form) sketched below: d dx (σ(x)) + ρa(x) = 0 PDE σ(x) = E du dx Hooke’s law (1) u(0) =?? essential BC σ(L) =?? natural BC where σ(x) is the axial stress in the rod, ρ= 2700kg /m3 is the mass density, and E = 70GPa is the Young’s modulus 1. Define appropriate BCs for the strong BVP 2. Find the solution of the strong BVP analytically 3. Derive the weak form of the BVP.arrow_forward
 Elements Of ElectromagneticsMechanical EngineeringISBN:9780190698614Author:Sadiku, Matthew N. O.Publisher:Oxford University Press
Elements Of ElectromagneticsMechanical EngineeringISBN:9780190698614Author:Sadiku, Matthew N. O.Publisher:Oxford University Press Mechanics of Materials (10th Edition)Mechanical EngineeringISBN:9780134319650Author:Russell C. HibbelerPublisher:PEARSON
Mechanics of Materials (10th Edition)Mechanical EngineeringISBN:9780134319650Author:Russell C. HibbelerPublisher:PEARSON Thermodynamics: An Engineering ApproachMechanical EngineeringISBN:9781259822674Author:Yunus A. Cengel Dr., Michael A. BolesPublisher:McGraw-Hill Education
Thermodynamics: An Engineering ApproachMechanical EngineeringISBN:9781259822674Author:Yunus A. Cengel Dr., Michael A. BolesPublisher:McGraw-Hill Education Control Systems EngineeringMechanical EngineeringISBN:9781118170519Author:Norman S. NisePublisher:WILEY
Control Systems EngineeringMechanical EngineeringISBN:9781118170519Author:Norman S. NisePublisher:WILEY Mechanics of Materials (MindTap Course List)Mechanical EngineeringISBN:9781337093347Author:Barry J. Goodno, James M. GerePublisher:Cengage Learning
Mechanics of Materials (MindTap Course List)Mechanical EngineeringISBN:9781337093347Author:Barry J. Goodno, James M. GerePublisher:Cengage Learning Engineering Mechanics: StaticsMechanical EngineeringISBN:9781118807330Author:James L. Meriam, L. G. Kraige, J. N. BoltonPublisher:WILEY
Engineering Mechanics: StaticsMechanical EngineeringISBN:9781118807330Author:James L. Meriam, L. G. Kraige, J. N. BoltonPublisher:WILEY





