
Concept explainers
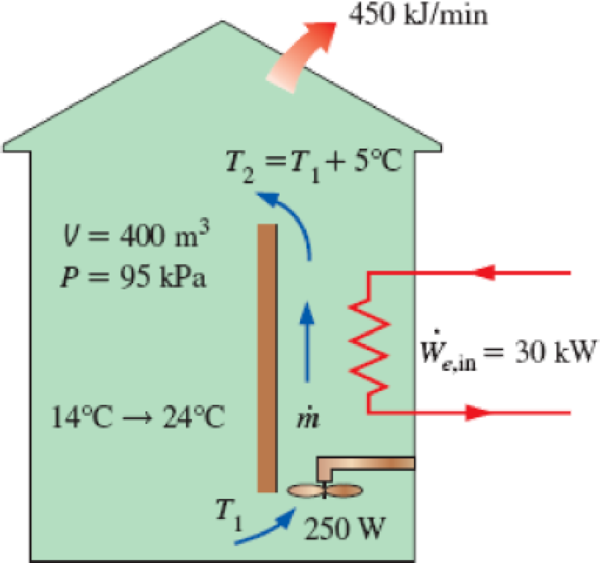
A building with an internal volume of 400 m3 is to be heated by a 30-kW electric resistance heater placed in the duct inside the building. Initially, the air in the building is at 14°C, and the local atmospheric pressure is 95 kPa. The building is losing heat to the surroundings at a steady rate of 450 kJ/min. Air is forced to flow through the duct and the heater steadily by a 250-W fan, and it experiences a temperature rise of 5°C each time it passes through the duct, which may be assumed to be adiabatic.
- (a) How long will it take for the air inside the building to reach an average temperature of 24°C?
- (b) Determine the average mass flow rate of air through the duct.
FIGURE P5–173
(a)
The time taken to attain the building’s average temperature of
Answer to Problem 173RP
The time taken to attain the building’s average temperature of
Explanation of Solution
Consider the entire building as system and the air circulates the in the building itself. There is no leakage to the surrounding.
The air flows at steady state through one inlet and one exit system (pipe and duct flow). Hence, the inlet and exit mass flow rates are equal.
Write the energy balance equation.
Here, the heat transfer is
In this system two work inputs are involved namely, the work input to the electric heater
The Equations (I) reduced as follows.
Here, there is no mass leakage from the building to the surrounding. The mass of air circulates in the building itself. Hence, inlet and exit enthalpies are neglected.
The change in internal energy is expresses as follow.
Here, the specific heat at constant volume is
Neglect the inlet and exit enthalpies and substitute
Equation (II).
Express the Equation (III) with respect to change of time and rearrange it to obtain
Write the formula for mass of air
The mass flow rate
Here, the change in time or time interval is
Refer Table A-1, “Molar mass, gas constant, and critical-point properties”.
The gas constant of air
Refer Table A-2, “Ideal-gas specific heats of various common gases”.
The specific heat at constant volume
Conclusion:
Substitute
Substitute
Substitute
Thus, the time taken to attain the building’s average temperature of
(b)
The average mass flow rate of air through the duct.
Answer to Problem 173RP
The average mass flow rate of air through the duct is
Explanation of Solution
Consider the heating duct with fan and heater only as the system. The air passes through in it steadily.
The system is at steady state. Hence, the rate of change in net energy of the system becomes zero.
The heating duct is an adiabatic duct. Hence, there is no heat loss.
The Equations (II) reduced as follows.
Express the Equation (VII) with respect to change of time as follows.
The change in enthalpy is expresses as follow.
Here, the specific heat at constant pressure is
Substitute
Refer Table A-2, “Ideal-gas specific heats of various common gases”.
The specific heat at constant pressure
Conclusion:
It is given that the temperature rise is
Substitute
Thus, The average mass flow rate of air through the duct is
Want to see more full solutions like this?
Chapter 5 Solutions
THERMODYNAMICS (LL)-W/ACCESS >CUSTOM<
- 3. A steel bar is pinned to a vertical support column by a 10 mm diameter hardened dowel pin, Figure 1. For P = 7500 N, find: a. the shear stress in the pin, b. the direct bearing stress on the hole in the bar, c. the minimum value of d to prevent tearout failure if the steel bar has a shear strength of 175 MPa. support column pin bar thickness of bar = 8 mm h d 150 mmarrow_forwardA press that delivers 115 strokes per minute, each stroke providing a force of 7826 N throughout a distance of 18 mm. The press efficiency is 90% and is driven by a 1749-rpm motor. Determine average torque that must be provided by the motor in the units of N-m.arrow_forward·3) find the force (P) for the figures (1) and (2) 15cm 10cm 15 h=10mm h2=6mm // Call = 90 N/2 P Agate Fig (i) Ans: 1)P=112614N 2) P=1956.5 N 25cm 25 cm الفترة أو الحجم تمر بالتي عثر اكو تورشن (ک Fig (2) h₁ = 10mm 42=6mm Cmarrow_forward
- 3. A steam power plant has an average monthly net power delivery of 740 MW over the course of a year. This power delivery is accomplished by burning coal in the boiler. The coal has a heating value of 9150 Btu/lbm. The cost of the coal is $14.20/ton. The overall thermal efficiency of the plant is, nth = Wnet Qboiler = 0.26 = 26% Determine the annual cost of the coal required to deliver the given average monthly power.arrow_forward47 14 16 12 34 10 12 12 33arrow_forward= The forces F₁ = 590 lb, F₂ = 380 lb, F3 = 240 lb and F 330 lb. Determine the forces in each member of the truss. Use positive values to indicate tension and negative values to indicate compression. a a a D b F₁ A 000 B. 779977 F₂V H G E F4 b BY NC SA 2013 Michael Swanbom Values for dimensions on the figure are given in the following table. Note the figure may not be to scale. Variable Value a 6 ft b 10.1 ft The force in member AB is lb. The force in member AH is lb. The force in member GH is lb. The force in member BH is lb. The force in member BC is lb. The force in member BG is lb. The force in member EG is lb. The force in member CD is lb. The force in member DE is lb. The force in member CE is lb. The force in member CG is lb.arrow_forward
- Multiple Choice Circle the best answer to each statement. 1. Which type of surface deviation is controlled by a cy- lindricity tolerance but not by a circularity tolerance? A. B. C. Ovality Taper Lobing D. None of the above 2. When verifying a cylindricity tolerance, the inspec- tion method must be able to collect a set of points and determine the: A. Distance between two coaxial cylinders that con- tain the set of points B. Cylinder that circumscribes the set of points C. Cylinder that inscribes the set of points D. Distance between two coaxial circles that contain the set of points 3. Where Rule #1 applies to a cylindrical regular feature of size, the tolerance value of a cylindricity tolerance applied to the feature of size must be tolerance. A. Less than B. Equal to C. Greater than D. None of the above the size 4. Which of the following modifiers may be applied with a cylindricity tolerance? A. M B. C. ℗ D. Ø 5. Which geometric tolerance can provide an indirect cylindricity…arrow_forwardThe beam AB is attached to the wall in the xz plane by a fixed support at A. A force of F = (−129î + 69.0ĵ + 3591) N is applied to the end of the beam at B. The weight of the beam can be modeled with a uniform distributed load of intensity w = 85.0 N/m acting in the negative z direction along its entire length. Find the support reactions at A. Z с A b a B F y Cc 10 BY NC SA 2016 Eric Davishahl X Values for dimensions on the figure are given in the following. table. Note the figure may not be to scale. Variable Value a 5.60 m b 5.00 m C 3.70 m A II = MA = ( m 2.> ~.> + + k) N k) N-arrow_forwardneed help?arrow_forward
 Elements Of ElectromagneticsMechanical EngineeringISBN:9780190698614Author:Sadiku, Matthew N. O.Publisher:Oxford University Press
Elements Of ElectromagneticsMechanical EngineeringISBN:9780190698614Author:Sadiku, Matthew N. O.Publisher:Oxford University Press Mechanics of Materials (10th Edition)Mechanical EngineeringISBN:9780134319650Author:Russell C. HibbelerPublisher:PEARSON
Mechanics of Materials (10th Edition)Mechanical EngineeringISBN:9780134319650Author:Russell C. HibbelerPublisher:PEARSON Thermodynamics: An Engineering ApproachMechanical EngineeringISBN:9781259822674Author:Yunus A. Cengel Dr., Michael A. BolesPublisher:McGraw-Hill Education
Thermodynamics: An Engineering ApproachMechanical EngineeringISBN:9781259822674Author:Yunus A. Cengel Dr., Michael A. BolesPublisher:McGraw-Hill Education Control Systems EngineeringMechanical EngineeringISBN:9781118170519Author:Norman S. NisePublisher:WILEY
Control Systems EngineeringMechanical EngineeringISBN:9781118170519Author:Norman S. NisePublisher:WILEY Mechanics of Materials (MindTap Course List)Mechanical EngineeringISBN:9781337093347Author:Barry J. Goodno, James M. GerePublisher:Cengage Learning
Mechanics of Materials (MindTap Course List)Mechanical EngineeringISBN:9781337093347Author:Barry J. Goodno, James M. GerePublisher:Cengage Learning Engineering Mechanics: StaticsMechanical EngineeringISBN:9781118807330Author:James L. Meriam, L. G. Kraige, J. N. BoltonPublisher:WILEY
Engineering Mechanics: StaticsMechanical EngineeringISBN:9781118807330Author:James L. Meriam, L. G. Kraige, J. N. BoltonPublisher:WILEY





