
Represent the maps given in Exercises 37-40 by graphs as we did in Example 6. Recall that we join two vertices by an edge if and only if the states that they represent share a stretch of common border
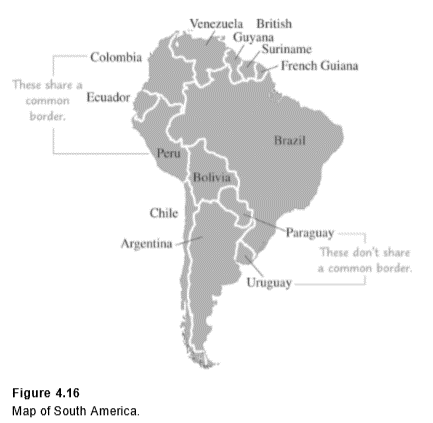
Example 6 Solving the Four-Color Problem for South America
Model the map of South America by a graph and use this graph to color the map using at most four colors.
Solution: In this problem, we have a set of countries, some of which are related in that they share a common border. Therefore, we can model this situation by a graph.
We will represent each country by a vertex; if two countries share a common border, we draw an edge between the corresponding vertices. This graph appears in Figure 4.17 .
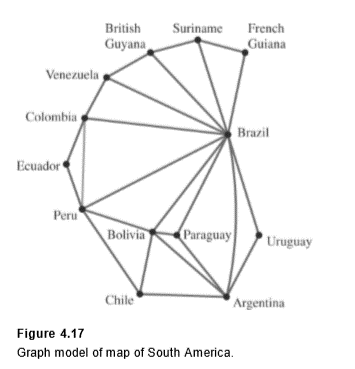
Note that we connect the vertices representing Peru and Colombia with an edge because they share a common boundary. We do not connect the vertices representing Argentina and Peru, because they have no boundary in common.
We can rephrase the map-coloring question now as follows: Using four or fewer colors, can we color the vertices of a graph so that no two vertices of the same edge receive the same color? It is easier to think about coloring a graph than it is to think about coloring the original map.
We show one coloring using four colors in Figure 4.18 and another coloring that I generated on my iPad using a graph theory app called Graphynx. Notice that Graphynx again had to use four colors to color the graph.
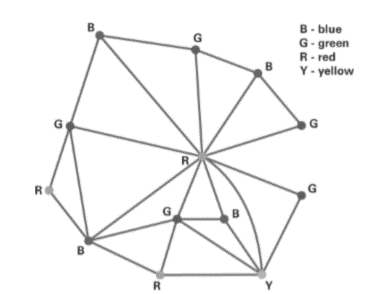
Figure 4.18 Coloring of graph of South America.
Graphynx coloring of graph of South America.
Want to see the full answer?
Check out a sample textbook solution
Chapter 4 Solutions
Mathematics All Around (6th Edition)
- 3. A different 7-Eleven has a bank of slurpee fountain heads. Their available flavors are as follows: Mountain Dew, Mountain Dew Code Red, Grape, Pepsi and Mountain Dew Livewire. You fill five different cups full with each type of flavor. How many different ways can you arrange the cups in a line if exactly two Mountain Dew flavors are next to each other? 3.2.1arrow_forwardBusinessarrow_forwardWhat is the area of this figure? 5 mm 4 mm 3 mm square millimeters 11 mm Submit 8 mm Work it out 9 mmarrow_forward
- No chatgpt pls will upvotearrow_forwardFind all solutions of the polynomial congruence x²+4x+1 = 0 (mod 143). (The solutions of the congruence x² + 4x+1=0 (mod 11) are x = 3,4 (mod 11) and the solutions of the congruence x² +4x+1 = 0 (mod 13) are x = 2,7 (mod 13).)arrow_forwardhttps://www.hawkeslearning.com/Statistics/dbs2/datasets.htmlarrow_forward
- Determine whether each function is an injection and determine whether each is a surjection.The notation Z_(n) refers to the set {0,1,2,...,n-1}. For example, Z_(4)={0,1,2,3}. f: Z_(6) -> Z_(6) defined by f(x)=x^(2)+4(mod6). g: Z_(5) -> Z_(5) defined by g(x)=x^(2)-11(mod5). h: Z*Z -> Z defined by h(x,y)=x+2y. j: R-{3} -> R defined by j(x)=(4x)/(x-3).arrow_forwardDetermine whether each function is an injection and determine whether each is a surjection.arrow_forwardLet A = {a, b, c, d}, B = {a,b,c}, and C = {s, t, u,v}. Draw an arrow diagram of a function for each of the following descriptions. If no such function exists, briefly explain why. (a) A function f : AC whose range is the set C. (b) A function g: BC whose range is the set C. (c) A function g: BC that is injective. (d) A function j : A → C that is not bijective.arrow_forward
 Discrete Mathematics and Its Applications ( 8th I...MathISBN:9781259676512Author:Kenneth H RosenPublisher:McGraw-Hill Education
Discrete Mathematics and Its Applications ( 8th I...MathISBN:9781259676512Author:Kenneth H RosenPublisher:McGraw-Hill Education Mathematics for Elementary Teachers with Activiti...MathISBN:9780134392790Author:Beckmann, SybillaPublisher:PEARSON
Mathematics for Elementary Teachers with Activiti...MathISBN:9780134392790Author:Beckmann, SybillaPublisher:PEARSON
 Thinking Mathematically (7th Edition)MathISBN:9780134683713Author:Robert F. BlitzerPublisher:PEARSON
Thinking Mathematically (7th Edition)MathISBN:9780134683713Author:Robert F. BlitzerPublisher:PEARSON Discrete Mathematics With ApplicationsMathISBN:9781337694193Author:EPP, Susanna S.Publisher:Cengage Learning,
Discrete Mathematics With ApplicationsMathISBN:9781337694193Author:EPP, Susanna S.Publisher:Cengage Learning, Pathways To Math Literacy (looseleaf)MathISBN:9781259985607Author:David Sobecki Professor, Brian A. MercerPublisher:McGraw-Hill Education
Pathways To Math Literacy (looseleaf)MathISBN:9781259985607Author:David Sobecki Professor, Brian A. MercerPublisher:McGraw-Hill Education





