
Concept explainers
Use the technique that we used in Example 7 to do Exercises 51–54. We do not list duplicate information in the tables.
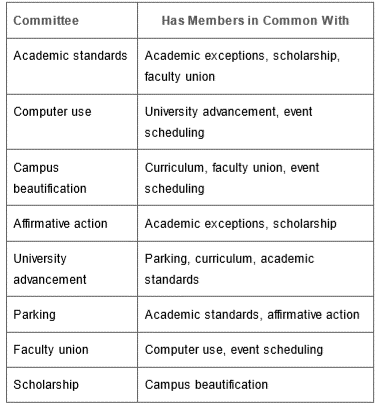
Scheduling meetings. A college’s student government has a number of committees that meet Tuesdays between 11:00 and 12:00. To avoid conflicts, it is important not to schedule two committee meetings at the same time if the two committees have students in common. Use the following table, which lists possible conflicts, to determine an acceptable schedule for the meetings.
Example 7 Using a Graph Theory Model to Schedule Committees
Each member of a city council usually serves on several committees to oversee the operation of various aspects of city government. Assume that council members serve on the following committees: police, parks, sanitation, finance, development, streets, fire department, and public relations. Use Table 4.1, which lists committees having common members, to determine a conflict-free schedule for the meetings. We do not duplicate information in Table 4.1. That is, because police conflicts with fire department, we do not also list that fire department conflicts with police.


Solution: Recall that in building a graph model, we must have two things:
A set of objects—in this case, the set of committees.1. A relationship among the objects. We will say that two committees are related if the two committees have members in common. So we can model the information in Table 4.1 by the graph in Figure 4.19.

This problem is similar to the map-coloring problem. If we color this graph, then all vertices having the same color represent committees that can meet at the same time. We show one possible coloring of the graph in Figure 4.1.
From Figure 4.19, we see that the police, streets, and sanitation committees have no common members and therefore can meet at the same time. Public relations, development, and the fire department can meet at a second time. Finance and parks can meet at a third time.
Want to see the full answer?
Check out a sample textbook solution
Chapter 4 Solutions
Mathematics All Around (6th Edition)
- II Consider the following data matrix X: X1 X2 0.5 0.4 0.2 0.5 0.5 0.5 10.3 10 10.1 10.4 10.1 10.5 What will the resulting clusters be when using the k-Means method with k = 2. In your own words, explain why this result is indeed expected, i.e. why this clustering minimises the ESS map.arrow_forwardX Acellus | Student admin192c.acellus.com go 0:0 Hannah wants to have concrete stairs for her backdoor. How much concrete will be needed to build the stairs? 20 cm 70 cm 30 cm 15 cm 10 cm 45 cm cm 70 cm GIF 自 لاarrow_forwardwhy the answer is 3 and 10?arrow_forward
- 1 Hannah wants to have concrete stairs for her backdoor. How much concrete will be needed to build the stairs? 70 cm 30 cm 15 cm 10 cm 10 cm 20 cm 45 cm cm³ GIF GIF/ 2 3 4 qwe asdf 5 6 自 yu ty u 8 ghjk 9 P Z X C cv b vbnm ×arrow_forwardPS 9 Two films are shown on screen A and screen B at a cinema each evening. The numbers of people viewing the films on 12 consecutive evenings are shown in the back-to-back stem-and-leaf diagram. Screen A (12) Screen B (12) 8 037 34 7 6 4 0 534 74 1645678 92 71689 Key: 116|4 represents 61 viewers for A and 64 viewers for B A second stem-and-leaf diagram (with rows of the same width as the previous diagram) is drawn showing the total number of people viewing films at the cinema on each of these 12 evenings. Find the least and greatest possible number of rows that this second diagram could have. TIP On the evening when 30 people viewed films on screen A, there could have been as few as 37 or as many as 79 people viewing films on screen B.arrow_forwardskip A swimming pool plan has concrete stairs leading down into the shallow end How much concrete will be needed to build the stairs? Bift 9 ft 2 ft 1 ft 9 ft 2 ft 5 ft [ ? ] ft³arrow_forward
 Glencoe Algebra 1, Student Edition, 9780079039897...AlgebraISBN:9780079039897Author:CarterPublisher:McGraw Hill
Glencoe Algebra 1, Student Edition, 9780079039897...AlgebraISBN:9780079039897Author:CarterPublisher:McGraw Hill Algebra: Structure And Method, Book 1AlgebraISBN:9780395977224Author:Richard G. Brown, Mary P. Dolciani, Robert H. Sorgenfrey, William L. ColePublisher:McDougal Littell
Algebra: Structure And Method, Book 1AlgebraISBN:9780395977224Author:Richard G. Brown, Mary P. Dolciani, Robert H. Sorgenfrey, William L. ColePublisher:McDougal Littell Mathematics For Machine TechnologyAdvanced MathISBN:9781337798310Author:Peterson, John.Publisher:Cengage Learning,
Mathematics For Machine TechnologyAdvanced MathISBN:9781337798310Author:Peterson, John.Publisher:Cengage Learning,- Algebra & Trigonometry with Analytic GeometryAlgebraISBN:9781133382119Author:SwokowskiPublisher:Cengage



