
Concept explainers
(a)
The maximum altitude.
(a)
Answer to Problem 65AP
The maximum altitude for this projectile motion is
Explanation of Solution
Draw the below figure for this condition as.
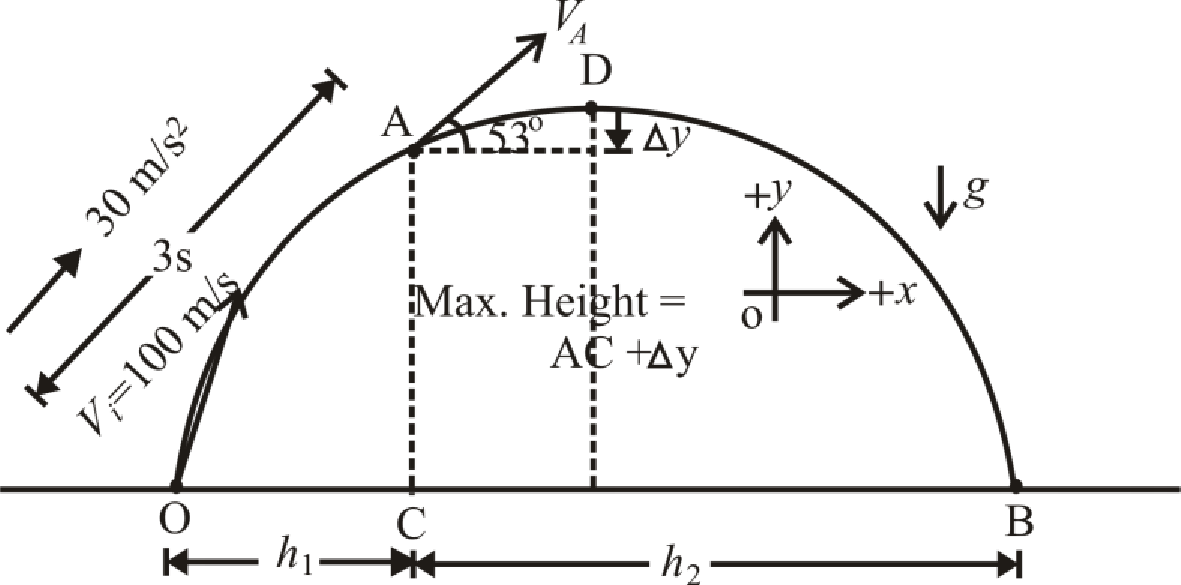
This is the case of projectile motion. Before the engine fails, car has acceleration up to distance from point
Write the expression for vertical acceleration as.
Here,
Write the expression for horizontal acceleration as.
Here,
Write the expression for initial velocity along vertical as.
Here,
Write the expression for initial velocity along horizontal as.
Here,
This projectile motion is divided into three part. Calculate the distances traveled during each phase of the motion.
Case:1
Refer to above figure at point
Write the expression for final velocity along vertical at point
Here,
Write the expression for final velocity along horizontal as.
Here,
Write the expression for vertical displacement as.
Here,
Write the expression for horizontal displacement as.
Here,
Case:2
Refer to the drawn figure, at point
Rearrange equation (V) in terms of time
Write the expression for horizontal distance cover by the engine as.
Write the expression for vertical distance cover by the engine as.
Write the expression for maximum altitude as.
Here,
Case:3
Refer to above figure, at point
Use third equation of motion to calculate the final velocity along verical at point
Write the expression for equation of motion at point
Conclusion:
Substitute
Substitute
Substitute
Substitute
Substitute
Substitute
Substitute
Substitute
Substitute
Substitute
Substitute
Substitute
Thus, the maximum altitude for this projectile motion is
(b)
The total time of fight.
(b)
Answer to Problem 65AP
The total time of flight is
Explanation of Solution
The acceleration is under gravity. The final velocity along vertical is downward direction at point
Write the expression for total time of flight as.
Here,
Write the expression for total flight time as.
Here,
Conclusion:
Substitute
Substitute
Substitute
Thus, the total time of flight is
(c)
The horizontal range.
(c)
Answer to Problem 65AP
The net horizontal range is
Explanation of Solution
Refer to above figure, the horizontal range can be calculated by the sum of distance
Write the expression for horizontal distance cover by the engine as.
Here,
Write the expression for horizontal range as.
Here
Conclusion:
Substitute
Substitute
Thus, the net horizontal range is
Want to see more full solutions like this?
Chapter 4 Solutions
Physics For Scientists And Engineers With Modern Physics, 9th Edition, The Ohio State University
- A circular capacitor has 6mm radius. Two parallel plates are 2mm apart. Between the capacitors magnetic field is B=410^-2 Tesla in theta direction at a given time. Calculate the displacement current and change in electric field at thatmomentarrow_forwardA light source is incoming with 30 degrees with the normal force to an equilateral prism made out of a material withn=1.2 and it exits the prism. Draw the ray diagramarrow_forward1 Cartpole System Analysis The cartpole system (Fig. 1) consists of a cart of mass M moving along a frictionless track, and a pendulum of mass m and length 1 pivoting around the cart. The mass of the pendulum is assumed to be equally distributed along the rigid rod. The system is actuated by a horizontal force F applied to the cart. m Ө X F M Figure 1: Cart-pole as the combination of a cart and a pendulum. 1.1 Tasks 1. Draw the free-body diagram of the pendulum and cart, showing all forces acting on them. Note: Point the reaction force Fx as the coupling force between the pendulum and the cart in positive x-direction in the free-body diagram of the pendulum.arrow_forward
- A light beam with intensity I=40W/m^2 passes through two polarizers. First polarizer makes 30 degrees with the y-axis and the second one makes 40 degrees with the x-axis. Find the final intensity as it exits both polarizers fora) Original beam is umpolarized b) Original beam is polarized in x direction c) Original beam is polarized in y-directonarrow_forwardFind the critical angle between ruby and glass. Ruby has n=1.75 and glass has n=1.5Draw an approximate raydiagram for a beam coming 5 degrees less than the critical anglearrow_forwardCalculate the value of the force F at which the 20 kg uniformly dense cabinet will start to tip. Calculate the acceleration of the cabinet at this force F. Must include the FBD and KD of the system. Ignore friction.arrow_forward
- 1) A 2.0 kg toy car travelling along a smooth horizontal surface experiences a horizontal force Fas shown in the picture to the left. Assuming the rightward direction to be positive and if the car has an initial velocity of 60.0m/s to the right, calculate the velocity of the car after the first 10.0s of motion. (Force is in Newtons and time in seconds). (Hint: Use impulse-momentum theorem) F 5.0 10 0 -10arrow_forward3) Two bumper cars of masses 600 kg and 900 kg travelling (on a smooth surface) with velocities 8m/s and 4 m/s respectively, have a head on collision. If the coefficient of restitution is 0.5. a) What sort of collision is this? b) Calculate their velocities immediately after collision. c) If the coefficient of restitution was 1 instead of 0.5, what is the amount of energy lost during collision?arrow_forwardThe rectangular loop of wire shown in the figure (Figure 1) has a mass of 0.18 g per centimeter of length and is pivoted about side ab on a frictionless axis. The current in the wire is 8.5 A in the direction shown. Find the magnitude of the magnetic field parallel to the y-axis that will cause the loop to swing up until its plane makes an angle of 30.0 ∘ with the yz-plane. Find the direction of the magnetic field parallel to the y-axis that will cause the loop to swing up until its plane makes an angle of 30.0 ∘ with the yz-plane.arrow_forward
- Give a more general expression for the magnitude of the torque τ. Rewrite the answer found in Part A in terms of the magnitude of the magnetic dipole moment of the current loop m. Define the angle between the vector perpendicular to the plane of the coil and the magnetic field to be ϕ, noting that this angle is the complement of angle θ in Part A. Give your answer in terms of the magnetic moment mm, magnetic field B, and ϕ.arrow_forwardCalculate the electric and magnetic energy densities at thesurface of a 3-mm diameter copper wire carrying a 15-A current. The resistivity ofcopper is 1.68×10-8 Ω.m.Prob. 18, page 806, Ans: uE= 5.6 10-15 J/m3 uB= 1.6 J/m3arrow_forwardA 15.8-mW laser puts out a narrow beam 2.0 mm in diameter.Suppose that the beam is in free space. What is the rms value of E in the beam? What isthe rms value of B in the beam?Prob. 28, page 834. Ans: Erms= 1380 V/m, Brms =4.59×10-6 Tarrow_forward
 Principles of Physics: A Calculus-Based TextPhysicsISBN:9781133104261Author:Raymond A. Serway, John W. JewettPublisher:Cengage Learning
Principles of Physics: A Calculus-Based TextPhysicsISBN:9781133104261Author:Raymond A. Serway, John W. JewettPublisher:Cengage Learning Glencoe Physics: Principles and Problems, Student...PhysicsISBN:9780078807213Author:Paul W. ZitzewitzPublisher:Glencoe/McGraw-Hill
Glencoe Physics: Principles and Problems, Student...PhysicsISBN:9780078807213Author:Paul W. ZitzewitzPublisher:Glencoe/McGraw-Hill Physics for Scientists and Engineers with Modern ...PhysicsISBN:9781337553292Author:Raymond A. Serway, John W. JewettPublisher:Cengage Learning
Physics for Scientists and Engineers with Modern ...PhysicsISBN:9781337553292Author:Raymond A. Serway, John W. JewettPublisher:Cengage Learning Physics for Scientists and EngineersPhysicsISBN:9781337553278Author:Raymond A. Serway, John W. JewettPublisher:Cengage Learning
Physics for Scientists and EngineersPhysicsISBN:9781337553278Author:Raymond A. Serway, John W. JewettPublisher:Cengage Learning Physics for Scientists and Engineers: Foundations...PhysicsISBN:9781133939146Author:Katz, Debora M.Publisher:Cengage Learning
Physics for Scientists and Engineers: Foundations...PhysicsISBN:9781133939146Author:Katz, Debora M.Publisher:Cengage Learning Physics for Scientists and Engineers, Technology ...PhysicsISBN:9781305116399Author:Raymond A. Serway, John W. JewettPublisher:Cengage Learning
Physics for Scientists and Engineers, Technology ...PhysicsISBN:9781305116399Author:Raymond A. Serway, John W. JewettPublisher:Cengage Learning





