Chapter 4, Problem 4.1P

Suppose we have a capacitance C discharging through a resistance R. Define and give an expression for the time constant. To attain a long time constant, do we need large or small values for R? For C?

To determine

The expression for the time constant of the discharging RC circuit and the magnitude of values of R and C for the condition of a large time constant.

Answer to Problem 4.1P

The expression for the time constant for the discharging RC circuit is given as $\tau =RC$.

The value of the values of R and C must be high for a large time constant.

Explanation of Solution

Given information:

Initially, the capacitor is fully charged, the charge on the plates of the capacitor at $t=0is{Q}_0$.

The capacitance of the capacitor is C, the resistance of the resistor is R and the time constant of the circuit is $\tau$.

Calculation:

The circuit diagram of the discharging RC circuit is shown below. The capacitor is initially fully charged. Since it is a discharging circuit, the charges on the plate of the capacitor are Q after a time $t$.

Applying K.V.L in loop 1

  

  $\begin{array}{l}{V}_R+V_C=\mathrm{0............}(1)\\ \end{array}$

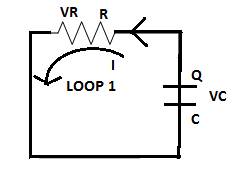
Let the charge on the capacitor at any instant is $Q_c$, the value of equation (1) at that instant is given as:

  $\begin{array}{l}IR+\frac{Q_c}{C}=0\\ \frac{d{Q}_c}{dt}R+\frac{Q_c}{C}=0\left\{\because I=\frac{d{Q}_c}{dt}\right\}\\ \frac{d{Q}_c}{dt}=-\frac{Q_c}{RC}\mathrm{..................}(2)\end{array}$

Solving the differential equation (2) using the variable separable method,

  $\begin{array}{l}-\frac{dt}{RC}=\frac{d{Q}_c}{Q_c}\mathrm{......................}(3)\\ \text{putting the limits in }\text{the}\text{ equation (3)}\\ -{\displaystyle \underset{0}{\overset{t}{\int }}\frac{dt}{RC}}={\displaystyle {\int }_{Q_0}^Q\frac{Q_c}{Q_c}}\\ \frac{-t}{RC}=\ln (\frac{Q}{Q_0})\\ e^{\frac{-t}{RC}}=e^{\ln (\frac{Q}{Q_0})}\\ e^{\frac{-t}{RC}}=\frac{Q}{Q_0}\\ Q=Q_0{e}^{\frac{-t}{RC}}\end{array}$

Where $Q_0$ is the charge on the plates of the capacitor at the time when the switch was on. The simplified equation for this circuit in terms of the time constant is shown below:

$Q=Q_0{e}^{\frac{-t}{\tau }}$ where, $\tau$ is the time constant of the given RC circuit.

  $\tau =RC$

Hence, the time constant is proportional to the values of resistance and capacitance in the circuit.

To attain a large time constant large value of R is needed as R is directly proportional to the time constant. Also, a large value of C is needed for a large time constant.