
Concept explainers
Consider the uniformly loaded simply supported steel beam with an overhang as shown. The second-area moment of the beam is I = 0.05 in4. Use superposition (with Table A–9 and the results of Prob. 4–20) to determine the reactions and the deflection equations of the beam. Plot the deflections.
Problem 4–21
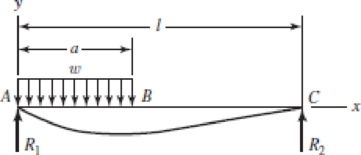
The net reaction at
The net reaction at
The expression for the deflection in the beam of portion
The expression for the deflection in the beam of portion
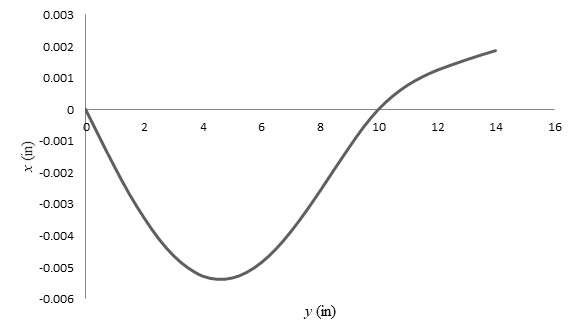
The plot of deflection verses length of the beam.
Answer to Problem 21P
The net reaction at
The net reaction at
The expression for the deflection in the beam of portion
The expression for the deflection in the beam of portion
The plot of deflection verses length of the beam is
Explanation of Solution
Write the expression for the reaction at
Here, the uniform load on the beam is
Write the expression for the reaction at
Here, the reaction at the
Write the expression for the deflection of the beam between
Here, the moment of inertia of the beam is
Write the expression for the slope of the deflection in the beam.
Substitute
Substitute
Write the expression for the deflection of the beam for
Substitute
Write the expression for the reaction at one end of the overhang section.
Here, the distance between
Write the expression for the reaction at other end of the overhang section.
Write the expression for the deflection in the beam section
Write the expression for the deflection in the beam section
Write the expression for the net reaction at
Write the expression for the net reaction at
Add equation (III) and (XI).
Add equation (VII) and (XII).
Conclusion:
Substitute
Substitute
Substitute
Substitute
Substitute
Thus, the net reaction at
Substitute
Thus, the net reaction at
Substitute
Thus, the expression for the deflection in the beam of portion
Substitute
Thus, the expression for the deflection in the beam of portion
Substitute different values of
Substitute
Substitute
Similarly,
Use excel spread sheet to calculate the
The Table-(1) shows the different values of the deflection at different point of the beam.
Table-(1)
| S. No. | length | deflection |
| 1 | ||
| 2 | ||
| 3 | ||
| 4 | ||
| 5 | ||
| 6 | ||
| 7 | ||
| 8 | ||
| 9 | ||
| 10 | ||
| 11 | ||
| 12 | ||
| 13 | ||
| 14 | ||
| 15 | ||
| 16 | ||
| 17 | ||
| 18 | ||
| 19 | ||
| 20 | ||
| 21 | ||
| 22 | ||
| 23 | ||
| 24 | ||
| 25 | ||
| 26 | ||
| 27 | ||
| 28 | ||
| 29 |
Draw the plot of length of the beam verses deflection of the beam.

Figure-(1)
Want to see more full solutions like this?
Chapter 4 Solutions
Shigley's Mechanical Engineering Design (McGraw-Hill Series in Mechanical Engineering)
- Consider the forces acting on the handle of the wrench in (Figure 1). a) Determine the moment of force F1={−F1={−2i+i+ 4 jj −−8k}lbk}lb about the zz axis. Express your answer in pound-inches to three significant figures. b) Determine the moment of force F2={F2={3i+i+ 7 jj −−6k}lbk}lb about the zz axis. Express your answer in pound-inches to three significant figures.arrow_forwardI need you to explain each and every step (Use paper)arrow_forwardCalculate the Moment About the Point A -20"- 5 lb 40 N D 1.5 m 40 N 4.5 m A 15 lb. 150 mm 52 N 5 12 100 mm 15 lb. 26 lb. 12 5 34 lb. 13 8 15 77777 36 lb.arrow_forward
- Calculate the Moment About the Point A -20"- 5 lb 40 N D 1.5 m 40 N 4.5 m A 15 lb. 150 mm 52 N 5 12 100 mm 15 lb. 26 lb. 12 5 34 lb. 13 8 15 77777 36 lb.arrow_forwardFormala for Hunzontal component= + cos & Vertical Component: Fsin t Find the vertical and horizontal components for the figure bellow: 30° 200 N 77 200 cos 30 = 173 N // 200 sin 30 = 100 N YA a₂+b₂ b₂ (b₁,b₂) a+b 20haits (a+b₁,a+b) Magnitude a and b a = lbl = 2o unite rugle of vector a wt Horisontal Axis = 30 11 vector & wt Honzontal Axis - 60° b b a= |a| Cas 30 a2 (a1, a2) ag = 10 bx = /b/ cos a 1 20 cos 80 = 17.32 Sia 30 = 20 sin 30. 60 = 10 = 20 Cos 60 = It by = 161 sin 60 = 20 sia 60 = 17.32 b₁ Rx ax +bx = 17.32 +10=2732 a₁ a₁+b₁ X By = ou + by= + + by = 10 + 17.32 =27.32 Magnitude = 38.637 Find the Vector a +b the Resultans The angle of the vector with the horizontal axle is 30 degrees while the angle of the vector b is 60 degrees. The magnitude of both vectors is 20 (units) angle of the Resultant vector = tam- " (14) 45arrow_forwardThe net force exerted on the piston by the exploding fuel-air mixture and friction is 5 kN to the left. A clockwise couple M = 200 N-m acts on the crank AB. The moment of inertia of the crank about A is 0.0003 kg-m2 . The mass of the connecting rod BC is 0.36 kg, and its center of mass is 40 mm from B on the line from B to C. The connecting rod’s moment of inertia about its center of mass is 0.0004 kg-m2 . The mass of the piston is 4.6 kg. The crank AB has a counterclockwise angular velocity of 2000 rpm at the instant shown. Neglect the gravitational forces on the crank, connecting rod, and piston – they still have mass, just don’t include weight on the FBDs. What is the piston’s acceleration?arrow_forward
- Solve only no 1 calculations,the one with diagram,I need handwritten expert solutionsarrow_forwardProblem 3 • Compute the coefficient matrix and the right-hand side of the n-parameter Ritz approximation of the equation d du (1+x)· = 0 for 0 < x < 1 dx dx u (0) = 0, u(1) = 1 Use algebraic polynomials for the approximation functions. Specialize your result for n = 2 and compute the Ritz coefficients.arrow_forwardFinite Element Analysis. Solve step by steparrow_forward
- Draw the top view In autoCAD from graphicsarrow_forwardAnswer all the calculations questions, if you are not not expert please don't attempt, don't use artificial intelligencearrow_forwardPlease measure the size of the following object, and then draw the front, top and side view in the AutoCAD (including the printing) just one arrow for this one 30arrow_forward
 Mechanics of Materials (MindTap Course List)Mechanical EngineeringISBN:9781337093347Author:Barry J. Goodno, James M. GerePublisher:Cengage Learning
Mechanics of Materials (MindTap Course List)Mechanical EngineeringISBN:9781337093347Author:Barry J. Goodno, James M. GerePublisher:Cengage Learning
