Chapter 4, Problem 33P

For the steel countershaft specified in the table, find the slope of the shaft at each bearing. Use superposition with the deflection equations in Table A–9. Assume the bearings constitute simple supports.

To determine

The slope of the shaft at each bearing.

Answer to Problem 33P

The slope of the shaft at bearing point O is $0.0128\text{rad}$ and the slope of the shaft at bearing point C is $0.0222\text{rad}$.

Explanation of Solution

Calculate the force $F_B$, using the net torque equation.

    $\begin{array}{c}{\displaystyle \sum T}=0\\ -\left(F_A\times \frac{d_A}{2}\times \cos {\theta }_1\right)+\left(F_B\times \frac{d_B}{2}\times \cos {\theta }_2\right)=0\\ F_B=F_A\frac{d_A\cos {\theta }_1}{d_B\cos {\theta }_2}\end{array}$                      (I)

Here, the force acting on pulley $A$ is $F_A$, the diameter of pulley $A$ is $d_A$, the angle at which force acts on pulley $A$ is ${\theta }_1$, the force acting on pulley $B$ is $F_B$, the diameter of pulley $B$ is $d_B$ and the angle at which force acts on pulley $B$ is ${\theta }_2$.

Write the equation for moment of inertia of the shaft.

    $I=\frac{\pi d^4}{64}$                                                (II)

Here, the diameter of the shaft is $d$.

The free body diagram of the beam in the direction of y-axis is shown below.

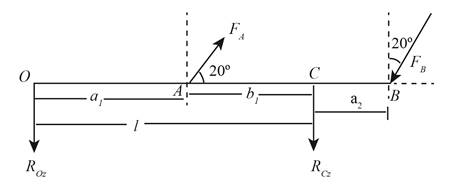
Figure (1)

Write the force component at point A along y-axis.

    $F_{Ay}=-F_A\cos 20°$

Write the force component at point B along y-axis.

    $F_{By}=F_B\sin 20°$

Write the deflection equation along y-axis for beam 6 and beam 10 using Table A-9.

    $y_{OA}=\frac{F_{Ay}{b}_{1}x}{6EIl}\left(x^2+b_1^2-l^2\right)+\frac{F_{By}{a}_{2}x}{6EIl}\left(l^2-x^2\right)$

Here, the force component at point A along y-axis is $F_{Ay}$ , the location of point A from the point C is $b_1$ , the distance of point A from left end is $x$ , the total length of the beam between point O point C is $l$ , Young modulus of the material is $E$ , moment of inertia of the beam is $I$ , the force component at point B along y-axis is $F_{By}$ and the location of point B from the point C is $a_2$.

Write the expression for net slope of the shaft along z-axis at point O.

    ${\left({\theta }_O\right)}_z={\left(\frac{d{y}_{OA}}{dx}\right)}_{x=0}$

Substitute $\frac{F_{Ay}{b}_{1}x}{6EIl}\left(x^2+b_1^2-l^2\right)+\frac{F_{By}{a}_{2}x}{6EIl}\left(l^2-x^2\right)$ for $y_{OA}$.

    $\begin{array}{c}{\left({\theta }_O\right)}_z={\left\{\frac{d}{dx}\cdot \frac{F_{Ay}{b}_{1}x}{6EIl}\left(x^2+b_1^2-l^2\right)+\frac{F_{By}{a}_{2}x}{6EIl}\left(l^2-x^2\right)\right\}}_{x=0}\\ ={\left\{\frac{1}{6EIl}\left[F_{Ay}{b}_1\left(3x^2+b_1^2-l^2\right)+F_{By}{a}_2\left(l^2-3x^2\right)\right]\right\}}_{x=0}\\ =\frac{1}{6EIl}\left[F_{Ay}{b}_1\left(3{\left(0\right)}^2+b_1^2-l^2\right)+F_{By}{a}_2\left(l^2-3{\left(0\right)}^2\right)\right]\\ =\frac{1}{6EIl}\left[F_{Ay}{b}_1\left(b_1^2-l^2\right)+F_{By}{a}_2{l}^2\right]\end{array}$

Substitute $-F_A\cos 20°$ for $F_{Ay}$ and $F_B\sin 20°$ for $F_{By}$.

    ${\left({\theta }_O\right)}_z=\frac{1}{6EIl}\left[\left(-F_A\cos 20°\right)b_1\left(b_1^2-l^2\right)+\left(F_B\sin 20°\right)a_2{l}^2\right]$                       (III)

The free body diagram of the beam in the direction of z-axis is shown below.

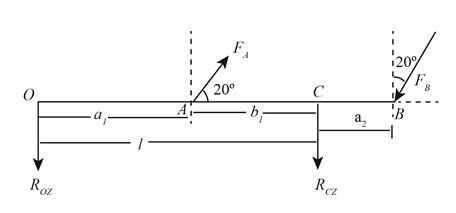
Figure (2)

Write the force component at point A along z-axis.

    $F_{Az}=F_A\sin 20°$

Write the force component at point B along z-axis.

    $F_{Bz}=-F_B\cos 20°$

Write the deflection equation along z-axis for beam 6 and beam 10 using Table A-9.

    $z_{OA}=\frac{F_{Az}{b}_{1}x}{6EIl}\left(x^2+b_1^2-l^2\right)+\frac{F_{Bz}{a}_{2}x}{6EIl}\left(l^2-x^2\right)$

Here, the force component at point A along z-axis is $F_{Az}$ and the force component at point B along z-axis is $F_{Bz}$.

Write the expression for net slope of the shaft along y-axis at point O.

    ${\left({\theta }_O\right)}_y=-{\left(\frac{d{z}_{OA}}{dx}\right)}_{x=0}$

Substitute $\frac{F_{Az}{b}_{1}x}{6EIl}\left(x^2+b_1^2-l^2\right)+\frac{F_{Bz}{a}_{2}x}{6EIl}\left(l^2-x^2\right)$ for $z_{OA}$.

    $\begin{array}{c}{\left({\theta }_O\right)}_y=-{\left\{\frac{d}{dx}\cdot \frac{F_{Az}{b}_{1}x}{6EIl}\left(x^2+b_1^2-l^2\right)+\frac{F_{Bz}{a}_{2}x}{6EIl}\left(l^2-x^2\right)\right\}}_{x=0}\\ =-{\left\{\frac{1}{6EIl}\left[F_{Az}{b}_1\left(3x^2+b_1^2-l^2\right)+F_{Bz}{a}_2\left(l^2-3x^2\right)\right]\right\}}_{x=0}\\ =-\frac{1}{6EIl}\left[F_{Az}{b}_1\left(3{\left(0\right)}^2+b_1^2-l^2\right)+F_{Bz}{a}_2\left(l^2-3{\left(0\right)}^2\right)\right]\\ =-\frac{1}{6EIl}\left[F_{Az}{b}_1\left(b_1^2-l^2\right)+F_{Bz}{a}_2{l}^2\right]\end{array}$

Substitute $F_A\sin 20°$ for $F_{Az}$ and $-F_B\cos 20°$ for $F_{Bz}$.

    ${\left({\theta }_O\right)}_y=-\frac{1}{6EIl}\left[\left(F_A\sin 20°\right)b_1\left(b_1^2-l^2\right)+\left(-F_B\cos 20°\right)a_2{l}^2\right]$               (IV)

Write the expression for the net slope at point O.

    ${\Theta }_O=\sqrt{{\left({\theta }_O\right)}_z^2+{\left({\theta }_O\right)}_y^2}$                                                                         (V)

Write the deflection equation along y-axis for section AC for beam 6 and beam 10 using Table A-9.

    $y_{AC}=\frac{F_{Ay}{a}_1\left(l-x\right)}{6EIl}\left(x^2+a_1^2-2lx\right)+\frac{F_{By}{a}_{2}x}{6EIl}\left(l^2-x^2\right)$

Here, the location of point A from point O is $a_1$.

Write the expression for net slope of the shaft along z-axis at point C.

    ${\left({\theta }_C\right)}_z={\left(\frac{d{y}_{AC}}{dx}\right)}_{x=l}$

Substitute $\frac{F_{Ay}{a}_1\left(l-x\right)}{6EIl}\left(x^2+a_1^2-2lx\right)+\frac{F_{By}{a}_{2}x}{6EIl}\left(l^2-x^2\right)$ for $y_{AC}$.

    $\begin{array}{c}{\left({\theta }_C\right)}_z={\left\{\frac{d}{dx}\cdot \frac{F_{Ay}{a}_1\left(l-x\right)}{6EIl}\left(x^2+a_1^2-2lx\right)+\frac{F_{By}{a}_{2}x}{6EIl}\left(l^2-x^2\right)\right\}}_{x=l}\\ ={\left\{\frac{1}{6EIl}\left[F_{Ay}{a}_1\left(6lx-2l^2-3x^2-a_1^2\right)+F_{By}{a}_2\left(l^2-3x^2\right)\right]\right\}}_{x=l}\\ =\frac{1}{6EIl}\left[F_{Ay}{a}_1\left(6l\cdot l-2l^2-3l^2-a_1^2\right)+F_{By}{a}_2\left(l^2-3l^2\right)\right]\\ =\frac{1}{6EIl}\left[F_{Ay}{a}_1\left(l^2-a_1^2\right)-2F_{By}{a}_2{l}^2\right]\end{array}$

Substitute $-F_A\cos 20°$ for $F_{Ay}$ and $F_B\sin 20°$ for $F_{By}$.

    ${\left({\theta }_C\right)}_z=\frac{1}{6EIl}\left[\left(-F_A\cos 20°\right)a_1\left(l^2-a_1^2\right)-2\left(F_B\sin 20°\right)a_2{l}^2\right]$                  (VI)

Write the deflection equation along z-axis for section AC for beam 6 and beam 10 using Table A-9.

    $z_{AC}=\frac{F_{Az}{a}_1\left(l-x\right)}{6EIl}\left(x^2+a_1^2-2lx\right)+\frac{F_{Bz}{a}_{2}x}{6EIl}\left(l^2-x^2\right)$

Write the expression for net slope of the shaft along z-axis at point C.

    ${\left({\theta }_C\right)}_y=-{\left(\frac{d{z}_{AC}}{dx}\right)}_{x=l}$

Substitute $\frac{F_{Az}{a}_1\left(l-x\right)}{6EIl}\left(x^2+a_1^2-2lx\right)+\frac{F_{Bz}{a}_{2}x}{6EIl}\left(l^2-x^2\right)$ for $z_{AC}$.

    $\begin{array}{c}{\left({\theta }_C\right)}_y=-{\left\{\frac{d}{dx}\cdot \frac{F_{Az}{a}_1\left(l-x\right)}{6EIl}\left(x^2+a_1^2-2lx\right)+\frac{F_{Bz}{a}_{2}x}{6EIl}\left(l^2-x^2\right)\right\}}_{x=l}\\ =-{\left\{\frac{1}{6EIl}\left[F_{Az}{a}_1\left(6lx-2l^2-3x^2-a_1^2\right)+F_{Bz}{a}_2\left(l^2-3x^2\right)\right]\right\}}_{x=l}\\ =-\frac{1}{6EIl}\left[F_{Az}{a}_1\left(6l\cdot l-2l^2-3l^2-a_1^2\right)+F_{Bz}{a}_2\left(l^2-3l^2\right)\right]\\ =-\frac{1}{6EIl}\left[F_{Az}{a}_1\left(l^2-a_1^2\right)-2F_{Bz}{a}_2{l}^2\right]\end{array}$

Substitute $F_A\sin 20°$ for $F_{Az}$ and $-F_B\cos 20°$ for $F_{Bz}$.

    ${\left({\theta }_C\right)}_y=-\frac{1}{6EIl}\left[\left(F_A\sin 20°\right)a_1\left(l^2-a_1^2\right)-2\left(-F_B\cos 20°\right)a_2{l}^2\right]$              (VII)

Write the expression for the net slope at point C.

    ${\Theta }_C=\sqrt{{\left({\theta }_C\right)}_z^2+{\left({\theta }_C\right)}_y^2}$                                                                            (VIII)

Conclusion:

Substitute $300\text{lbf}$ for $F_A$, $20\text{in}$ for $d_A$, $20°$ for ${\theta }_1$, $8\text{in}$ for $d_B$ and $20°$ for ${\theta }_2$ in Equation (I).

    $\begin{array}{c}{F}_B=300\text{lbf}\times \frac{20\cos 20°}{8\cos 20°}\\ =750\text{lbf}\end{array}$

Substitute $1.25\text{in}$ for $d$ in Equation (II).

    $\begin{array}{c}I=\frac{\pi \times {\left(1.25\text{in}\right)}^4}{64}\\ =0.1198{\text{in}}^{\text{4}}\end{array}$

Substitute $300\text{lbf}$ for $F_A$, $14\text{in}$ for $b_1$, $30\text{in}$ for $l$, $30\times {10}^6\text{psi}$ for $E$, $0.1198{\text{in}}^{\text{4}}$ for $I$, $750\text{lbf}$ for $F_B$ and $9\text{in}$ for $a_2$ in Equation (III).

    $\begin{array}{c}{\left({\theta }_O\right)}_z=\frac{1}{6\left(30\times {10}^6\text{psi}\right)\left(0.1198{\text{in}}^4\right)\left(30\text{in}\right)}\left[\begin{array}{l}\left(-300\text{lbf}\times \cos 20°\right)\left(14\text{in}\right)\left({\left(14\text{in}\right)}^2-{\left(30\text{in}\right)}^2\right)\\ +\left(750\text{lbf}\times \sin 20°\right)\left(9\text{in}\right){\left(30\text{in}\right)}^2\end{array}\right]\\ =0.00751\text{rad}\end{array}$

Thus, the slope of the shaft at bearing point O along z-axis is $0.00751\text{rad}$.

Substitute $300\text{lbf}$ for $F_A$, $14\text{in}$ for $b_1$, $30\text{in}$ for $l$, $30\times {10}^6\text{psi}$ for $E$, $0.1198{\text{in}}^{\text{4}}$ for $I$, $750\text{lbf}$ for $F_B$ and $9\text{in}$ for $a_2$ in Equation (IV).

    $\begin{array}{c}{\left({\theta }_O\right)}_y=-\frac{1}{6\left(30\times {10}^6\text{psi}\right)\left(0.1198{\text{in}}^4\right)\left(30\right)}\left[\begin{array}{l}\left(300\text{lbf}\times \sin 20°\right)\left(14\text{in}\right)\left({\left(14\text{in}\right)}^2-{\left(30\text{in}\right)}^2\right)\\ +\left(-750\text{lbf}\times \cos 20°\right)\left(9\text{in}\right){\left(30\text{in}\right)}^2\end{array}\right]\\ =0.01039\text{rad}\\ \approx 0.0104\text{rad}\end{array}$

Thus, the slope of the shaft at bearing point O along y-axis is $0.0104\text{rad}$.

Substitute $0.00751\text{rad}$ for ${\left({\theta }_O\right)}_z$ and $0.0104\text{rad}$ for ${\left({\theta }_O\right)}_y$ in Equation (V).

    $\begin{array}{c}{\Theta }_O=\sqrt{{\left(0.00751\text{rad}\right)}^2+{\left(0.0104\text{rad}\right)}^2}\\ =0.01283\text{rad}\\ \approx 0.0128\text{rad}\end{array}$

Thus, the net slope of the shaft at bearing point O is $0.0128\text{rad}$.

Substitute $300\text{lbf}$ for $F_A$, $16\text{in}$ for $a_1$, $30\text{in}$ for $l$, $30\times {10}^6\text{psi}$ for $E$, $0.1198{\text{in}}^{\text{4}}$ for $I$, $750\text{lbf}$ for $F_B$ and $9\text{in}$ for $a_2$ in Equation (VI).

    $\begin{array}{c}{\left({\theta }_C\right)}_z=\frac{1}{6\left(30\times {10}^6\text{psi}\right)\left(0.1198{\text{in}}^4\right)\left(30\right)}\left[\begin{array}{l}\left(-300\text{lbf}\times \cos 20°\right)\left(16\text{in}\right)\left({\left(30\text{in}\right)}^2-{\left(16\text{in}\right)}^2\right)\\ -2\left(750\text{lbf}\times \sin 20°\right)\left(9\text{in}\right){\left(30\text{in}\right)}^2\end{array}\right]\\ =-0.0109\text{rad}\end{array}$

Thus, the slope of the shaft at bearing point C along z-axis is $-0.0109\text{rad}$.

Substitute $300\text{lbf}$ for $F_A$, $16\text{in}$ for $b_1$, $30\text{in}$ for $l$, $30\times {10}^6\text{psi}$ for $E$, $0.1198{\text{in}}^{\text{4}}$ for $I$, $750\text{lbf}$ for $F_B$ and $9\text{in}$ for $a_2$ in Equation (VII).

    $\begin{array}{c}{\left({\theta }_C\right)}_y=-\frac{1}{6\left(30\times {10}^6\text{psi}\right)\left(0.1198{\text{in}}^4\right)\left(30\right)}\left[\begin{array}{l}\left(300\text{lbf}\times \sin 20°\right)\left(16\text{in}\right)\left({\left(30\text{in}\right)}^2-{\left(16\text{in}\right)}^2\right)\\ -2\left(-750\text{lbf}\times \cos 20°\right)\left(9\text{in}\right){\left(30\text{in}\right)}^2\end{array}\right]\\ =-0.0193\text{rad}\end{array}$

Thus, the slope of the shaft at bearing point O along y-axis is $-0.0193\text{rad}$.

Substitute $-0.0109\text{rad}$ for ${\left({\theta }_C\right)}_z$ and $-0.0193\text{rad}$ for ${\left({\theta }_C\right)}_y$ in Equation (VIII).

    $\begin{array}{c}{\Theta }_C=\sqrt{{\left(-0.0109\text{rad}\right)}^2+{\left(-0.0193\text{rad}\right)}^2}\\ =0.02216\text{rad}\\ \approx 0.0222\text{rad}\end{array}$

Thus, the net slope of the shaft at bearing point C is $0.0222\text{rad}$.