Chapter 4, Problem 32P

To determine

The slope of the shaft at each bearing.

Answer to Problem 32P

The slope of the shaft at bearing point O is $0.00750\text{rad}$ and the slope of the shaft at bearing point C is $0.00558\text{rad}$.

Explanation of Solution

The figure below shows the free body diagram of pulley A.

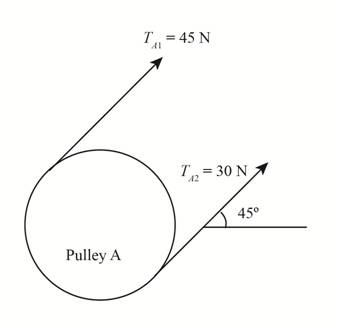
Figure (1)

The figure below shows the free body diagram of pulley B.

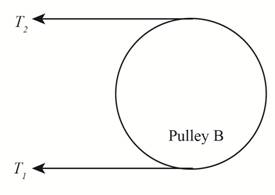
Figure (2)

The given assumption is that the belt tension on the loose side is $15\%$ of the tension on the tight side.

Write the expression for the tensions on the loose side in terms of tension on the tight side.

$T_2=0.15T_1$ (I)

Here, the tension on the tight side is $T_1$ and the tension on the loose side is $T_2$.

Write the equation to balance the tension on the counter shaft.

$\begin{array}{c}{\displaystyle \sum T}=0\\ \left(T_{A1}-T_{A2}\right)\frac{d_A}{2}-\left(T_2-T_1\right)\frac{d_B}{2}=0\end{array}$ (II)

Here, the tension on the tight side of pulley $A$ is $T_{A1}$, the tension on the loose side of pulley $A$ is $T_{A2}$, diameter of shaft $A$ is $d_A$ and the diameter of shaft $B$ is $d_B$.

Substitute $0.15T_1$ for $T_2$ in Equation (II).

$\begin{array}{c}\left(T_{A1}-T_{A2}\right)\frac{d_A}{2}+\left(0.15T_1-T_1\right)\frac{d_B}{2}=0\\ T_1=\frac{1}{0.85}\left(\left(T_{A1}-T_{A2}\right)\frac{d_A}{d_B}\right)\end{array}$ (III)

Write the expression for net applied load at point A.

$F_A=\left(T_{A1}+T_{A2}\right)$ (IV)

Here, the tension force exerted by the pulley at each side at point A are $T_{A1}$ and $T_{A2}$ respectively.

Write the expression for net applied load at point B.

$F_B=T_1+T_2$ (V)

Here, the tension force exerted by the pulley at each side at point B are $T_1$ and $T_2$ respectively.

Write the equation for moment of inertia of the shaft.

$I=\frac{\pi d^4}{64}$ (VI)

Here, the diameter of the shaft is $d$.

The free body diagram of the beam in the direction of y-axis is shown below.

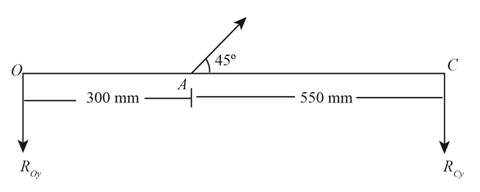
Figure (3)

Write the equation for force component along y-axis.

$F_{Ay}=F_A\sin 45°$

Here, the net force at point A is $F_A$.

Write the equation for force component along z-axis.

$F_{Az}=-F_A\cos 45°$

Write the deflection equation for portion OA using Table A-9 for beam 6.

$y_{OA}=\frac{F_{Ay}{b}_{1}x}{6EIl}\left(x^2+b_1^2-l^2\right)$

Here, Young’s modulus of the shaft material is $E$, , the location of applied point load at point A from right end bearing point C is $b_1$ and the distance of any given section from left end is $x$.

Substitute $F_A\sin 45°$ for $F_{Ay}$ in the above Equation.

$y_{OA}=\frac{\left(F_A\sin 45°\right)b_{1}x}{6EIl}\left(x^2+b_1^2-l^2\right)$

Write the expression for net slope of the shaft at point O along z-axis.

${\left({\theta }_O\right)}_z={\left(\frac{d{y}_{OA}}{dx}\right)}_{x=0}$

Substitute $\frac{\left(F_A\sin 45°\right)b_{1}x}{6EIl}\left(x^2+b_1^2-l^2\right)$ for $y_{OA}$.

$\begin{array}{c}{\left({\theta }_O\right)}_z={\left\{\frac{d}{dx}\cdot \frac{\left(F_A\sin 45°\right)b_{1}x}{6EIl}\left(x^2+b_1^2-l^2\right)\right\}}_{x=0}\\ ={\left\{\frac{1}{6EIl}\left[\left(F_A\sin 45°\right)b_1\left(3x^2+b_1^2-l^2\right)\right]\right\}}_{x=0}\\ =\frac{1}{6EIl}\left[\left(F_A\sin 45°\right)b_1\left(3{\left(0\right)}^2+b_1^2-l^2\right)\right]\\ =\frac{\left(F_A\sin 45°\right)b_1}{6EIl}\left(b_1^2-l^2\right)\end{array}$ (VII)

The free body diagram of the beam in the direction of z-axis is shown below.

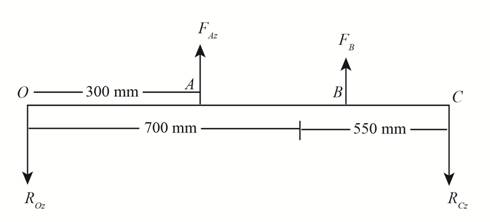
Figure (4)

Write the deflection equation along z-axis using Table A-9 for beam 6.

$z_{OA}=\frac{F_{Az}{b}_{1}x}{6EIl}\left(x^2+b_1^2-l^2\right)+\frac{F_B{b}_{2}x}{6EIl}\left(x^2+b_2^2-l^2\right)$

Here, the force component along z-axis is $F_{Az}$ , the net force at point B is $F_B$ , the location of applied point load at point B from right end bearing point C is $b_2$ and the distance of any given section from left end is $x$.

Write the expression for net slope of the shaft at point O along y-axis.

${\left({\theta }_O\right)}_y=-{\left(\frac{d{z}_{OB}}{dx}\right)}_{x=0}$

Substitute $\frac{F_{Az}{b}_{1}x}{6EIl}\left(x^2+b_1^2-l^2\right)+\frac{F_B{b}_{2}x}{6EIl}\left(x^2+b_2^2-l^2\right)$ for $z_{OB}$.

$\begin{array}{c}{\left({\theta }_O\right)}_y=-{\left\{\frac{d}{dx}\cdot \frac{F_{Az}{b}_{1}x}{6EIl}\left(x^2+b_1^2-l^2\right)+\frac{F_B{b}_{2}x}{6EIl}\left(x^2+b_2^2-l^2\right)\right\}}_{x=0}\\ =-{\left\{\frac{1}{6EIl}\left[F_{Az}{b}_1\left(3x^2+b_1^2-l^2\right)+F_B{b}_2\left(3x^2+b_2^2-l^2\right)\right]\right\}}_{x=0}\\ =-\frac{1}{6EIl}\left[F_{Az}{b}_1\left(3{\left(0\right)}^2+b_1^2-l^2\right)+F_B{b}_2\left(3{\left(0\right)}^2+b_2^2-l^2\right)\right]\\ =-\frac{F_{Az}{b}_1}{6EIl}\left(b_1^2-l^2\right)-\frac{F_B{b}_2}{6EIl}\left(b_2^2-l^2\right)\end{array}$

Substitute $-F_A\cos 45°$ for $F_{Az}$ in the above Equation.

${\left({\theta }_O\right)}_y=-\frac{\left(-F_A\cos 45°\right)b_1}{6EIl}\left(b_1^2-l^2\right)-\frac{F_B{b}_2}{6EIl}\left(b_2^2-l^2\right)$ (VIII)

Write the expression for net slope at point O.

${\Theta }_O=\sqrt{{\left({\theta }_O\right)}_z^2+{\left({\theta }_O\right)}_y^2}$ (IX)

Write the deflection equation for portion BC using Table A-9 for beam 6.

$y_{BC}=\frac{F_{Ay}{a}_1\left(l-x\right)}{6EIl}\left(x^2+a_1^2-2lx\right)$

Here, the location of applied point load at point A from left end bearing point O is $a_1$ and the distance of any given section from left end is $x$.

Write the expression for net slope of the shaft at point C along z-axis.

${\left({\theta }_C\right)}_z={\left(\frac{d{y}_{BC}}{dx}\right)}_{x=l}$

Substitute $\frac{F_{Ay}{a}_1\left(l-x\right)}{6EIl}\left(x^2+a_1^2-2lx\right)$ for $y_{BC}$.

$\begin{array}{c}{\left({\theta }_C\right)}_z={\left\{\frac{d}{dx}\cdot \frac{F_{Ay}{a}_1\left(l-x\right)}{6EIl}\left(x^2+a_1^2-2lx\right)\right\}}_{x=l}\\ ={\left\{\frac{1}{6EIl}\left[F_{Ay}{a}_1\left(6lx-2l^2-3x^2-a_1^2\right)\right]\right\}}_{x=l}\\ =\frac{1}{6EIl}\left[F_{Ay}{a}_1\left(6l\cdot l-2l^2-3l^2-a_1^2\right)\right]\\ =\frac{F_{Ay}{a}_1}{6EIl}\left(l^2-a_1^2\right)\end{array}$

Substitute $F_A\sin 45°$ for $F_{Ay}$ in the above Equation.

${\left({\theta }_C\right)}_z=\frac{\left(F_A\sin 45°\right)a_1}{6EIl}\left(l^2-a_1^2\right)$ (X)

Write the deflection equation for portion BC using Table A-9 for beam 6.

$z_{BC}=\frac{F_{Az}{a}_1\left(l-x\right)}{6EIl}\left(x^2+a_1^2-2lx\right)+\frac{F_B{a}_2\left(l-x\right)}{6EIl}\left(x^2+a_2^2-2lx\right)$

Here, the location of applied point load at point B from left end bearing point O is $a_2$ and the distance of any given section from left end is $x$.

Write the expression for net slope of the shaft at point C along y-axis.

${\left({\theta }_C\right)}_y=-{\left(\frac{d{z}_{BC}}{dx}\right)}_{x=l}$

Substitute the value of $z_{BC}$.

$\begin{array}{c}{\left({\theta }_C\right)}_y=-{\left\{\frac{d}{dx}\cdot \frac{F_{Az}{a}_1\left(l-x\right)}{6EIl}\left(x^2+a_1^2-2lx\right)+\frac{F_B{a}_2\left(l-x\right)}{6EIl}\left(x^2+a_2^2-2lx\right)\right\}}_{x=l}\\ =-{\left\{\frac{1}{6EIl}\left[F_{Az}{a}_1\left(6lx-2l^2-3x^2-a_1^2\right)+F_B{a}_2\left(6lx-2l^2-3x^2-a_2^2\right)\right]\right\}}_{x=l}\\ =-\frac{1}{6EIl}\left[F_{Az}{a}_1\left(6l\cdot l-2l^2-3l^2-a_1^2\right)+F_B{a}_2\left(6l\cdot l-2l^2-3l^2-a_2^2\right)\right]\\ =-\frac{F_{Az}{a}_1}{6EIl}\left(l^2-a_1^2\right)-\frac{F_B{a}_2}{6EIl}\left(l^2-a_2^2\right)\end{array}$

Substitute $-F_A\cos 45°$ for $F_{Az}$ in the above Equation.

${\left({\theta }_C\right)}_y=-\frac{\left(-F_A\cos 45°\right)a_1}{6EIl}\left(l^2-a_1^2\right)-\frac{F_B{a}_2}{6EIl}\left(l^2-a_2^2\right)$ (XI)

Write the expression for net slope at point C.

${\Theta }_C=\sqrt{{\left({\theta }_C\right)}_z^2+{\left({\theta }_C\right)}_y^2}$ . (XII)

Conclusion:

Substitute $300\text{N}$ for $T_{A1}$, $45\text{N}$ for $T_{A2}$, $250\text{mm}$ for $d_A$ and $300\text{mm}$ for $d_B$  in Equation (III).

$\begin{array}{c}{T}_1=\frac{1}{0.85}\left(\left(300\text{N}-45\text{N}\right)\times \frac{250\text{mm}}{300\text{mm}}\right)\\ =\frac{1}{0.85}\left(212.5\text{N}\right)\\ =250\text{N}\end{array}$

Substitute $250\text{N}$ for $T_1$ in Equation (I)

$\begin{array}{c}{T}_2=0.15\left(250\text{N}\right)\\ =37.5\text{N}\end{array}$

Substitute $300\text{N}$ for $T_{A1}$ and $45\text{N}$ for $T_{A2}$ in Equation (IV).

$\begin{array}{c}{F}_A=\left(300\text{N}+45\text{N}\right)\\ =345\text{N}\end{array}$

Substitute $250\text{N}$ for $T_1$ and $37.5\text{N}$ for $T_2$ in Equation (V).

$\begin{array}{c}{F}_B=250\text{N}+37.5\text{N}\\ =287.5\text{N}\end{array}$

Substitute $20\text{mm}$ for $d$ in Equation (VI).

$\begin{array}{c}I=\frac{\pi {\left(20\text{mm}\right)}^4}{64}\\ =7854{\text{mm}}^{\text{4}}\end{array}$

Substitute $-345\text{N}$ for $F_A$ , $550\text{mm}$ for $b_1$ , $850\text{mm}$ for $l$ , $207\times {10}^3\text{MPa}$ for $E$ and $7854{\text{mm}}^{\text{4}}$ for $I$ in Equation (VII).

$\begin{array}{c}{\left({\theta }_O\right)}_z=\frac{\left(\left(-345\text{N}\right)\sin 45°\right)\left(550\text{mm}\right)}{6\left(207\times {10}^3\text{MPa}\right)\left(7854{\text{mm}}^4\right)\left(850\text{mm}\right)}\left({\left(550\text{mm}\right)}^2-{\left(850\text{mm}\right)}^2\right)\\ =\left[\left(-1.618\times {10}^{-8}\text{1}/{\text{mm}}^2\right)\left(-42000{\text{mm}}^2\right)\right]\\ =0.00680\text{rad}\end{array}$

Thus, the slope of the shaft at bearing point O along z-axis is $0.00680\text{rad}$.

Substitute $-345\text{N}$ for $F_A$ , $550\text{mm}$ for $b_1$ , $850\text{mm}$ for $l$ , $207\times {10}^3\text{MPa}$ for $E$ and $7854{\text{mm}}^{\text{4}}$ for $I$ and $150\text{mm}$ for $b_2$ in Equation (VIII).

$\begin{array}{c}{\left({\theta }_O\right)}_y=\left[\begin{array}{l}-\frac{\left(\left(-345\text{N}\right)\cos 45°\right)\left(550\text{mm}\right)\left({\left(550\text{mm}\right)}^2-{\left(850\text{mm}\right)}^2\right)}{6\left(207\times {10}^3\text{MPa}\right)\left(7854{\text{mm}}^4\right)\left(850\text{mm}\right)}\\ -\frac{\left(287.5\text{N}\right)\left(150\text{mm}\right)}{6\left(207\times {10}^3\text{MPa}\right)\left(7854{\text{mm}}^4\right)\left(850\text{mm}\right)}\left({\left(150\text{mm}\right)}^2-{\left(850\text{mm}\right)}^2\right)\end{array}\right]\\ =\left[-\left(0.00680\text{rad}\right)-\left(-3.6426\times {10}^{-3}\text{rad}\right)\right]\\ \approx -0.00316\text{rad}\end{array}$

Thus, the slope of the shaft at bearing point O along y-axis is $-0.00316\text{rad}$.

Substitute $0.00680\text{rad}$ for ${\left({\theta }_O\right)}_z$ and $-0.00316\text{rad}$ for ${\left({\theta }_O\right)}_y$ in Equation (IX).

$\begin{array}{c}{\Theta }_O=\sqrt{{\left(0.00680\text{rad}\right)}^2+{\left(-0.00316\text{rad}\right)}^2}\\ =\sqrt{5.622\times {10}^{-5}{\text{rad}}^2}\\ \approx 0.00750\text{rad}\end{array}$

Thus, the net slope of the shaft at bearing point O is $0.00750\text{rad}$.

Substitute $345\text{N}$ for $F_A$ , $300\text{mm}$ for $a_1$ , $850\text{mm}$ for $l$ , $207\times {10}^3\text{MPa}$ for $E$ and $7854{\text{mm}}^{\text{4}}$ for $I$ in Equation (X).

$\begin{array}{c}{\left({\theta }_C\right)}_z=\frac{\left(\left(345\text{N}\right)\sin 45°\right)\left(300\text{mm}\right)}{6\left(207\times {10}^3\text{}\text{MPa}\right)\left(7854{\text{mm}}^4\right)\left(850\text{mm}\right)}\left({\left(850\text{mm}\right)}^2-{\left(300\text{mm}\right)}^2\right)\\ =\left[\left(8.83\times {10}^{-9}\text{1}/{\text{mm}}^2\right)\left(632500{\text{mm}}^2\right)\right]\\ =0.00558\text{rad}\end{array}$

Thus, the slope of the shaft at bearing point C along z-axis is $0.00558\text{rad}$.

Substitute $345\text{N}$ for $F_A$, $550\text{mm}$ for $b_1$, $850\text{mm}$ for $l$, $207\times {10}^3\text{MPa}$ for $E$, $7854{\text{mm}}^{\text{4}}$ for $I$ and $150\text{mm}$ for $b_2$ in Equation (XI).

$\begin{array}{c}{\left({\theta }_C\right)}_y=\left[\begin{array}{l}-\frac{\left(-345\cos 45°\right)\left(300\right)}{6\left(207\times {10}^3\right)\left(7854\right)\left(850\right)}\left({850}^2-{300}^2\right)\\ -\frac{\left(287.5\right)\left(700\right)}{6\left(207\times {10}^3\right)\left(7854\right)\left(850\right)}\left({850}^2-{700}^2\right)\end{array}\right]\\ =-6.04\times {10}^{-5}\text{rad}\end{array}$

Thus, the slope of the shaft at bearing point C along y-axis is $-6.04\times {10}^{-5}\text{rad}$.

Substitute $0.00558\text{rad}$ for ${\left({\theta }_C\right)}_z$ and $-6.04\times {10}^{-5}\text{rad}$ for ${\left({\theta }_C\right)}_y$ in Equation (XII).

$\begin{array}{c}{\Theta }_C=\sqrt{{\left(0.00558\text{rad}\right)}^2+{\left(-6.04\times {10}^{-5}\text{rad}\right)}^2}\\ =\sqrt{3.11\times {10}^{-5}{\text{rad}}^2}\\ =0.00558\text{rad}\end{array}$

Thus, the net slope of the shaft at bearing point C is $0.00558\text{rad}$.