
Concept explainers
(a) If
(b) What condition on
(a)
The relationship must hold between
Answer to Problem 1RE
The function
The function
The function
Explanation of Solution
The function
For example:
Now, draw the graph of
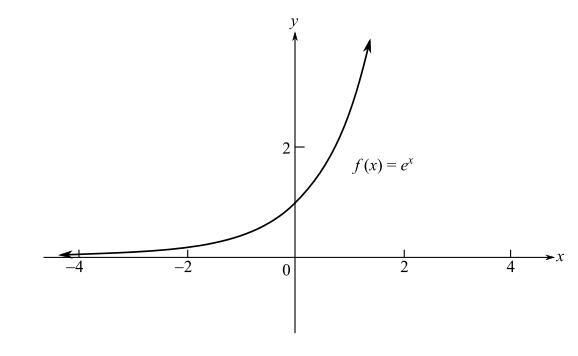
It can be observed from the graph that the function value is increasing, if
The function
For example:
Now, draw the graph of
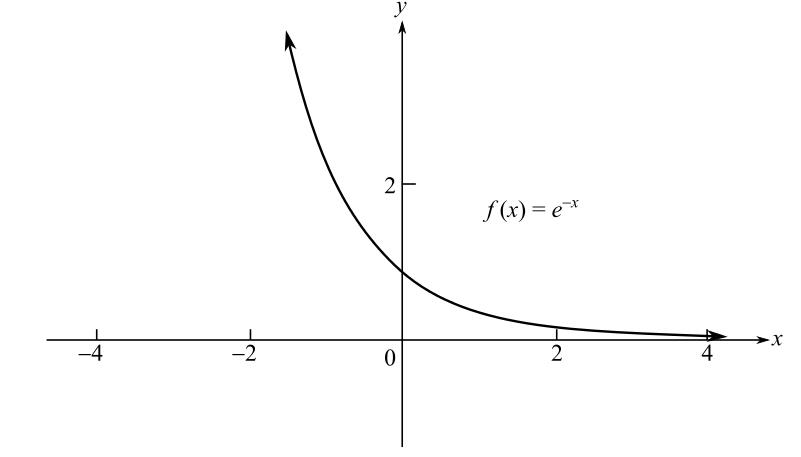
It can be observed from the graph that the function value is decreasing if
The function
Now, draw the graph of

It can be observed from the graph that the function value is constant if
(b)
The condition on
Answer to Problem 1RE
If
If
If
Explanation of Solution
Consider the given statement.
If
Consider the example
So,
If
Consider the example
So,
If
Consider the example
So,
Want to see more full solutions like this?
Chapter 4 Solutions
Calculus Early Transcendentals, Binder Ready Version
Additional Math Textbook Solutions
University Calculus: Early Transcendentals (4th Edition)
Elementary Statistics: Picturing the World (7th Edition)
Algebra and Trigonometry (6th Edition)
Elementary and Intermediate Algebra: Concepts and Applications (7th Edition)
Elementary Statistics Using The Ti-83/84 Plus Calculator, Books A La Carte Edition (5th Edition)
- for the given rectangular coordinates, find two sets of polar coordinates for which 0≤θ<2π, one with r>0 and the other with r<0. (-2sqrt(3),9)arrow_forwardI circled the correct answer, could you show me how to do it using divergence and polar coordinatesarrow_forwardThe correct answer is D Could you explain and show the steps pleasearrow_forward
- Taylor Series Approximation Example- H.W More terms used implies better approximation f(x) 4 f(x) Zero order f(x + 1) = f(x;) First order f(x; + 1) = f(x;) + f'(x;)h 1.0 Second order 0.5 True f(x + 1) = f(x) + f'(x)h + ƒ"(x;) h2 2! f(x+1) 0 x; = 0 x+1 = 1 x h f(x)=0.1x4-0.15x³- 0.5x2 -0.25x + 1.2 51 Taylor Series Approximation H.w: Smaller step size implies smaller error Errors f(x) + f(x,) Zero order f(x,+ 1) = f(x) First order 1.0 0.5 Reduced step size Second order True f(x + 1) = f(x) + f'(x)h f(x; + 1) = f(x) + f'(x)h + "(xi) h2 f(x,+1) O x₁ = 0 x+1=1 Using Taylor Series Expansion estimate f(1.35) with x0 =0.75 with 5 iterations (or & s= 5%) for f(x)=0.1x 0.15x³-0.5x²- 0.25x + 1.2 52arrow_forwardCould you explain this using the formula I attached and polar coorindatesarrow_forwardCould you explain this using the formula I attached and polar coordinatesarrow_forward
- 2 prove that Dxy #Dx Dyarrow_forwardEXAMPLE 3 Find S X √√2-2x2 dx. SOLUTION Let u = 2 - 2x². Then du = Χ dx = 2- 2x² = 信 du dx, so x dx = du and u-1/2 du (2√u) + C + C (in terms of x).arrow_forwardLet g(z) = z-i z+i' (a) Evaluate g(i) and g(1). (b) Evaluate the limits lim g(z), and lim g(z). 2-12 (c) Find the image of the real axis under g. (d) Find the image of the upper half plane {z: Iz > 0} under the function g.arrow_forward
- k (i) Evaluate k=7 k=0 [Hint: geometric series + De Moivre] (ii) Find an upper bound for the expression 1 +2x+2 where z lies on the circle || z|| = R with R > 10. [Hint: Use Cauchy-Schwarz]arrow_forward21. Determine for which values of m the function (x) = x™ is a solution to the given equation. a. 3x2 d²y dx² b. x2 d²y +11x dy - 3y = 0 dx dy dx2 x dx 5y = 0arrow_forwardhelp me solve thisarrow_forward
- Algebra & Trigonometry with Analytic GeometryAlgebraISBN:9781133382119Author:SwokowskiPublisher:Cengage

 Big Ideas Math A Bridge To Success Algebra 1: Stu...AlgebraISBN:9781680331141Author:HOUGHTON MIFFLIN HARCOURTPublisher:Houghton Mifflin Harcourt
Big Ideas Math A Bridge To Success Algebra 1: Stu...AlgebraISBN:9781680331141Author:HOUGHTON MIFFLIN HARCOURTPublisher:Houghton Mifflin Harcourt  Algebra: Structure And Method, Book 1AlgebraISBN:9780395977224Author:Richard G. Brown, Mary P. Dolciani, Robert H. Sorgenfrey, William L. ColePublisher:McDougal Littell
Algebra: Structure And Method, Book 1AlgebraISBN:9780395977224Author:Richard G. Brown, Mary P. Dolciani, Robert H. Sorgenfrey, William L. ColePublisher:McDougal Littell Glencoe Algebra 1, Student Edition, 9780079039897...AlgebraISBN:9780079039897Author:CarterPublisher:McGraw Hill
Glencoe Algebra 1, Student Edition, 9780079039897...AlgebraISBN:9780079039897Author:CarterPublisher:McGraw Hill Trigonometry (MindTap Course List)TrigonometryISBN:9781337278461Author:Ron LarsonPublisher:Cengage Learning
Trigonometry (MindTap Course List)TrigonometryISBN:9781337278461Author:Ron LarsonPublisher:Cengage Learning





