Chapter 3.P2, Problem 1P

If $x_j(t)$ represents the amount of drug (milligrams) in compartment $j$, $j=1,2$, use Figure 3.P.3 and the mass balance law

$\frac{d{x}_j}{dt}=\text{compartment}j\text{input}\text{rate}-\text{compartment}j\text{output}\text{rate}$, (i)

to show that $x_1$ and $x_2$ satisfy the system

$\frac{d{x}_1}{dt}=-\left(K+k_{21}\right)x_1+k_{21}{x}_2+d(t)$

$\frac{d{x}_2}{dt}=k_{21}{x}_1-k_{12}{x}_2$. (ii)

To determine

To prove: $x_1$ and $x_2$ satisfy the system $\frac{d{x}_1}{dt}=-(K+k_{21})x_1+k_{12}{x}_2+d(t)$, $\frac{d{x}_2}{dt}=k_{21}{x}_1-k_{12}{x}_2$ where $x_j(t)$ represents the amount of drug (milligrams) in compartment $j,j=1,2$, by using the figure:

and the mass balance law $\frac{d{x}_j}{dt}=$ compartment $j$ input rate $-$ compartment $j$ output rate.

Explanation of Solution

Given information:

$x_j(t)$ represents the amount of drug (milligrams) in compartment $j,j=1,2$, by using the figure:

Formula used:

Mass balance law $\frac{d{x}_j}{dt}=$ compartment $j$ input rate $-$ compartment $j$ output rate.

Proof:

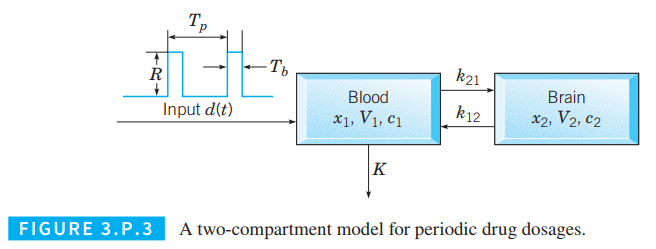
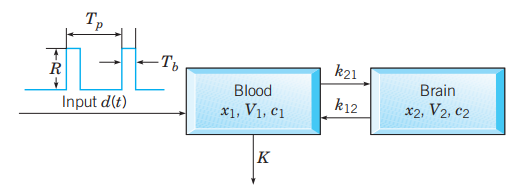
Let the rate constant $k_{21}$ is the fraction per unit time of the drug in the blood transferred to the brain, and $k_{12}$ is the fraction per unit time of the drug in the brain transferred to the blood.

Therefore, the input rate of the compartment $1$ with blood is given by,

compartment $1$ input rate $=d(t)+x_2{k}_{12}$

As $K$ is the rate at which drug is removed from the blood,

Therefore, the output rate of the drug from the compartment $1$ is given as,

compartment $1$ output rate $=K{x}_1+x_1{k}_{21}$.

By using mass balance law,

$\frac{d{x}_1}{dt}=$ compartment $1$ input rate $-$ compartment $1$ output rate.

$\Rightarrow \frac{d{x}_1}{dt}=d(t)+x_2{k}_{12}-\left(K{x}_1+x_1{k}_{21}\right)$

$\Rightarrow \frac{d{x}_1}{dt}=-\left(K+k_{21}\right)x_1+x_2{k}_{12}+d(t)$

From the given figure, the input rate of the compartment $2$ with blood is given by,

compartment $2$ input rate $=k_{21}{x}_1$

Also, the output rate of the drug from the compartment $2$ is given as,

compartment $2$ output rate $=k_{12}{x}_2$.

By using mass balance law,

$\frac{d{x}_2}{dt}=$ compartment $2$ input rate $-$ compartment $2$ output rate.

$\Rightarrow \frac{d{x}_2}{dt}=k_{21}{x}_1-k_{12}{x}_2$.

$\Rightarrow \frac{d{x}_2}{dt}=-\left(K+k_{21}\right)x_1+x_2{k}_{12}+d(t)$.

Therefore, $x_1$ and $x_2$ satisfy the system $\frac{d{x}_1}{dt}=-(K+k_{21})x_1+k_{12}{x}_2+d(t)$, $\frac{d{x}_2}{dt}=k_{21}{x}_1-k_{12}{x}_2$.