Chapter 3.2, Problem 31P

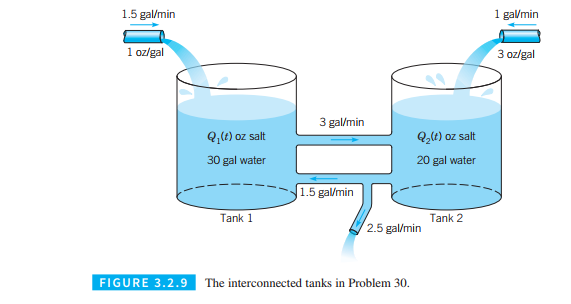
Consider two interconnected tanks similar to those on Figure 3.2.9. Tank $1$ initially contains $60\text{gal}$ of water and $Q_1{}^{0}oz$ of salt, and Tank $2$ initially contains $100\text{gal}$ of water and $Q_2{}^0\text{oz}$ of salt. Water containing $q_{1}oz/gal$ of salt flows into Tank $1$ at a rate of $3\text{gal/min}$. The mixture in Tank $1$ flows out at a rate of $4\text{gal/min}$, of which half flows into Tank $2$, while the remainder leaves the system. Water containing $q_2\text{oz/gal}$ of salt also flows into Tank $2$ from the outside at the rate of $1\text{gal/min}$. The mixture in Tank $2$ leaves the tank at a rate of $3\text{gal/min}$, of which some flows back into Tank $1$ at a rate of $1\text{gal/min}$, while the rest leaves the system.

(a) Draw a diagram that depicts the flow process described above. Let $Q_1\left(t\right)$ and $Q_2\left(t\right)$, respectively, be the amount of salt in each tank at time $t$. Write down differential equations and initial conditions for $Q_1$ and $Q_2$ that model the flow process.

(b) Find the equilibrium values $Q_1{}^E$ and $Q_2{}^E$ in terms of the concentrations $q_1$ and $q_2$.

(c) Is it possible (by adjusting $q_1$ and $q_2$) to obtain $Q_1{}^E=60$ and $Q_2{}^E=50$ as an equilibrium state?

(d) Describe which equilibrium states are possible for this system for various values of $q_1$ and $q_2$.