Precalculus: Mathematics for Calculus - 6th Edition
6th Edition
ISBN: 9780840068071
Author: Stewart, James, Redlin, Lothar, Watson, Saleem
Publisher: Cengage Learning
expand_more
expand_more
format_list_bulleted
Videos
Textbook Question
Chapter 3.7, Problem 85E
Drug Concentration A drug is administered to a patient, and the concentration of the drug in the bloodstream is monitored. At time t ≥ 0 (in hours since giving the drug) the concentration (in mg/L) is given by
Graph the function c with a graphing device.
- (a) What is the highest concentration of drug that is reached in the patient’s bloodstream?
- (b) What happens to the drug concentration after a long period of time?
- (c) How long does it take for the concentration to drop below 0.3 mg/L?
(a)
Expert Solution
To determine
The highest concentration of drug that is reached in the patient’s bloodstream.
Answer to Problem 85E
The highest concentration of drug reached in the patient’s bloodstream is 2.5 mg/L.
Explanation of Solution
Given:
The drug concentration in the bloodstream is given below,
Where tis the time in hours since giving the drug c is the concentration of drug in bloodstream in mg/L.
Calculation:
The given rational function is
Sketch the graph of given rational function by graphing device,
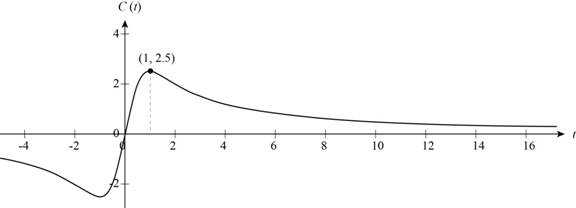
Figure (1)
The highest concentration of drug is the maximum point in graph of rational function.
From the graph, the local maximum is
(b)
Expert Solution
To determine
The drug concentration after a long period of time.
Explanation of Solution
From the Figure (1), it can be noticed that the graph of rational function decreases at the time increases.
Thus, the concentration of drug decreases to 0 after a long period of time.
(c)
Expert Solution
To determine
The time for the concentration to drop below 0.3 mg/L.
Answer to Problem 85E
The time for the concentration to drop below 0.3 mg/L is 16.6 hours.
Explanation of Solution
Given:
The drug concentration in the bloodstream is given below,
Where t is the time in hours since giving the drug and c is the concentration of drug in bloodstream in mg/L.
Calculation:
Substitute 0.3 for
Solve the above quadratic equation by following formula which is used to find the solutions for x if the quadratic equation is
Substitute t for x, 5 for b, 0.3 for c and 0.3 for a in above given formula,
Take positive sign first and find the value of t,
Take negative sign and find the value of t,
From the Figure (1), the value of t, where the concentration drops below 0.3 mg/L is 16.6.
Thus, the time for the concentration to drop below 0.3 mg/L is 16.6 hours.
Chapter 3 Solutions
Precalculus: Mathematics for Calculus - 6th Edition
Ch. 3.1 - To put the quadratic function f(x)=ax2+bx+c in...Ch. 3.1 - The quadratic function f(x) = a(x - h)2 + k is in...Ch. 3.1 - The graph of f(x) = 3(x - 2)2 - 6 is a parabola...Ch. 3.1 - The graph of f(x) = -3(x - 2)2 - 6 is a parabola...Ch. 3.1 - Prob. 5ECh. 3.1 - Prob. 6ECh. 3.1 - Prob. 7ECh. 3.1 - Prob. 8ECh. 3.1 - Prob. 9ECh. 3.1 - Prob. 10E
Ch. 3.1 - Prob. 11ECh. 3.1 - Prob. 12ECh. 3.1 - Prob. 13ECh. 3.1 - Prob. 14ECh. 3.1 - Prob. 15ECh. 3.1 - Prob. 16ECh. 3.1 - Prob. 17ECh. 3.1 - Prob. 18ECh. 3.1 - Prob. 19ECh. 3.1 - Prob. 20ECh. 3.1 - Prob. 21ECh. 3.1 - Prob. 22ECh. 3.1 - Prob. 23ECh. 3.1 - Prob. 24ECh. 3.1 - Prob. 25ECh. 3.1 - Prob. 26ECh. 3.1 - Prob. 27ECh. 3.1 - Prob. 28ECh. 3.1 - Prob. 29ECh. 3.1 - Prob. 30ECh. 3.1 - Prob. 31ECh. 3.1 - Prob. 32ECh. 3.1 - Prob. 33ECh. 3.1 - Prob. 34ECh. 3.1 - Prob. 35ECh. 3.1 - Prob. 36ECh. 3.1 - Prob. 37ECh. 3.1 - Prob. 38ECh. 3.1 - Prob. 39ECh. 3.1 - Prob. 40ECh. 3.1 - Prob. 41ECh. 3.1 - Prob. 42ECh. 3.1 - Prob. 43ECh. 3.1 - Prob. 44ECh. 3.1 - Prob. 45ECh. 3.1 - Prob. 46ECh. 3.1 - Prob. 47ECh. 3.1 - Prob. 48ECh. 3.1 - Prob. 49ECh. 3.1 - Prob. 50ECh. 3.1 - Prob. 51ECh. 3.1 - Prob. 52ECh. 3.1 - Prob. 53ECh. 3.1 - Prob. 54ECh. 3.1 - Prob. 55ECh. 3.1 - Prob. 56ECh. 3.1 - Prob. 57ECh. 3.1 - Prob. 58ECh. 3.1 - Prob. 59ECh. 3.1 - Prob. 60ECh. 3.1 - Prob. 61ECh. 3.1 - Prob. 62ECh. 3.1 - Height of a Ball If a ball is thrown directly...Ch. 3.1 - Path of a Ball A ball is thrown across a playing...Ch. 3.1 - Revenue A manufacturer finds that the revenue...Ch. 3.1 - Sales A soft-drink vendor at a popular beach...Ch. 3.1 - Advertising The effectiveness of a television...Ch. 3.1 - Pharmaceuticals When a certain drug is taken...Ch. 3.1 - Agriculture The number of apples produced by each...Ch. 3.1 - Agriculture At a certain vineyard it is found that...Ch. 3.1 - Prob. 71ECh. 3.1 - Prob. 72ECh. 3.1 - Prob. 73ECh. 3.1 - Prob. 74ECh. 3.1 - Fencing a Horse Corral Carol has 2400 ft of...Ch. 3.1 - Making a Rain Gutter A rain gutter is formed by...Ch. 3.1 - Stadium Revenue A baseball team plays in a stadium...Ch. 3.1 - Prob. 78ECh. 3.1 - Prob. 79ECh. 3.1 - Prob. 80ECh. 3.2 - Prob. 1ECh. 3.2 - Prob. 2ECh. 3.2 - Prob. 3ECh. 3.2 - Which of the following statements couldnt possibly...Ch. 3.2 - Prob. 5ECh. 3.2 - Prob. 6ECh. 3.2 - Prob. 7ECh. 3.2 - Prob. 8ECh. 3.2 - Prob. 9ECh. 3.2 - Prob. 10ECh. 3.2 - Prob. 11ECh. 3.2 - Prob. 12ECh. 3.2 - Prob. 13ECh. 3.2 - Prob. 14ECh. 3.2 - Prob. 15ECh. 3.2 - Prob. 16ECh. 3.2 - Prob. 17ECh. 3.2 - Prob. 18ECh. 3.2 - Prob. 19ECh. 3.2 - Prob. 20ECh. 3.2 - Prob. 21ECh. 3.2 - Prob. 22ECh. 3.2 - Prob. 23ECh. 3.2 - Prob. 24ECh. 3.2 - Prob. 25ECh. 3.2 - Prob. 26ECh. 3.2 - Prob. 27ECh. 3.2 - Prob. 28ECh. 3.2 - Prob. 29ECh. 3.2 - Prob. 30ECh. 3.2 - Prob. 31ECh. 3.2 - Prob. 32ECh. 3.2 - Prob. 33ECh. 3.2 - Prob. 34ECh. 3.2 - Prob. 35ECh. 3.2 - Prob. 36ECh. 3.2 - Prob. 37ECh. 3.2 - Prob. 38ECh. 3.2 - Prob. 39ECh. 3.2 - Prob. 40ECh. 3.2 - Prob. 41ECh. 3.2 - Prob. 42ECh. 3.2 - Prob. 43ECh. 3.2 - Prob. 44ECh. 3.2 - Prob. 45ECh. 3.2 - Prob. 46ECh. 3.2 - Prob. 47ECh. 3.2 - Prob. 48ECh. 3.2 - Prob. 49ECh. 3.2 - Prob. 50ECh. 3.2 - Prob. 51ECh. 3.2 - Prob. 52ECh. 3.2 - Prob. 53ECh. 3.2 - Prob. 54ECh. 3.2 - Prob. 55ECh. 3.2 - Prob. 56ECh. 3.2 - Prob. 57ECh. 3.2 - Prob. 58ECh. 3.2 - Prob. 59ECh. 3.2 - Prob. 60ECh. 3.2 - Prob. 61ECh. 3.2 - Prob. 62ECh. 3.2 - Prob. 63ECh. 3.2 - Prob. 64ECh. 3.2 - Prob. 65ECh. 3.2 - Prob. 66ECh. 3.2 - Prob. 67ECh. 3.2 - Prob. 68ECh. 3.2 - Prob. 69ECh. 3.2 - Prob. 70ECh. 3.2 - Prob. 71ECh. 3.2 - Prob. 72ECh. 3.2 - Prob. 73ECh. 3.2 - Prob. 74ECh. 3.2 - Prob. 75ECh. 3.2 - Prob. 76ECh. 3.2 - Prob. 77ECh. 3.2 - Prob. 78ECh. 3.2 - Prob. 79ECh. 3.2 - Prob. 80ECh. 3.2 - Market Research A market analyst working for a...Ch. 3.2 - Population Change The rabbit population on a small...Ch. 3.2 - Volume of a Box An open box is to be constructed...Ch. 3.2 - Volume of a Box A cardboard box has a square base,...Ch. 3.2 - Prob. 85ECh. 3.2 - Prob. 86ECh. 3.2 - Prob. 87ECh. 3.2 - Prob. 88ECh. 3.3 - If we divide the polynomial P by the factor x c...Ch. 3.3 - (a) If we divide the polynomial P(x) by the factor...Ch. 3.3 - Prob. 3ECh. 3.3 - Prob. 4ECh. 3.3 - Prob. 5ECh. 3.3 - Prob. 6ECh. 3.3 - Prob. 7ECh. 3.3 - Prob. 8ECh. 3.3 - Prob. 9ECh. 3.3 - Prob. 10ECh. 3.3 - Prob. 11ECh. 3.3 - Prob. 12ECh. 3.3 - Prob. 13ECh. 3.3 - Prob. 14ECh. 3.3 - Prob. 15ECh. 3.3 - Prob. 16ECh. 3.3 - Prob. 17ECh. 3.3 - Prob. 18ECh. 3.3 - Prob. 19ECh. 3.3 - Prob. 20ECh. 3.3 - Prob. 21ECh. 3.3 - Prob. 22ECh. 3.3 - Prob. 23ECh. 3.3 - Prob. 24ECh. 3.3 - Prob. 25ECh. 3.3 - Prob. 26ECh. 3.3 - Prob. 27ECh. 3.3 - Prob. 28ECh. 3.3 - Prob. 29ECh. 3.3 - Prob. 30ECh. 3.3 - Prob. 31ECh. 3.3 - Prob. 32ECh. 3.3 - Prob. 33ECh. 3.3 - Prob. 34ECh. 3.3 - Prob. 35ECh. 3.3 - Prob. 36ECh. 3.3 - Prob. 37ECh. 3.3 - Prob. 38ECh. 3.3 - Prob. 39ECh. 3.3 - Prob. 40ECh. 3.3 - Prob. 41ECh. 3.3 - Prob. 42ECh. 3.3 - Prob. 43ECh. 3.3 - Prob. 44ECh. 3.3 - Prob. 45ECh. 3.3 - Prob. 46ECh. 3.3 - Prob. 47ECh. 3.3 - Prob. 48ECh. 3.3 - Prob. 49ECh. 3.3 - Prob. 50ECh. 3.3 - Prob. 51ECh. 3.3 - Prob. 52ECh. 3.3 - Prob. 53ECh. 3.3 - Prob. 54ECh. 3.3 - Prob. 55ECh. 3.3 - Prob. 56ECh. 3.3 - Prob. 57ECh. 3.3 - Prob. 58ECh. 3.3 - Prob. 59ECh. 3.3 - Prob. 60ECh. 3.3 - Prob. 61ECh. 3.3 - Prob. 62ECh. 3.3 - Prob. 63ECh. 3.3 - Prob. 64ECh. 3.3 - Prob. 65ECh. 3.3 - Prob. 66ECh. 3.3 - Prob. 67ECh. 3.3 - Prob. 68ECh. 3.3 - Prob. 69ECh. 3.3 - Prob. 70ECh. 3.4 - If the polynomial function...Ch. 3.4 - Using Descartes Rule of Signs, we can tell that...Ch. 3.4 - True or False? If c is a real zero of the...Ch. 3.4 - True or False? If a is an upper bound for the real...Ch. 3.4 - Prob. 5ECh. 3.4 - Prob. 6ECh. 3.4 - Prob. 7ECh. 3.4 - Prob. 8ECh. 3.4 - Prob. 9ECh. 3.4 - Prob. 10ECh. 3.4 - Prob. 11ECh. 3.4 - Prob. 12ECh. 3.4 - Prob. 13ECh. 3.4 - Prob. 14ECh. 3.4 - Prob. 15ECh. 3.4 - Prob. 16ECh. 3.4 - Prob. 17ECh. 3.4 - Prob. 18ECh. 3.4 - Prob. 19ECh. 3.4 - Prob. 20ECh. 3.4 - Prob. 21ECh. 3.4 - Prob. 22ECh. 3.4 - Prob. 23ECh. 3.4 - Prob. 24ECh. 3.4 - Prob. 25ECh. 3.4 - Prob. 26ECh. 3.4 - Prob. 27ECh. 3.4 - Prob. 28ECh. 3.4 - Prob. 29ECh. 3.4 - Prob. 30ECh. 3.4 - Prob. 31ECh. 3.4 - Prob. 32ECh. 3.4 - Prob. 33ECh. 3.4 - Prob. 34ECh. 3.4 - Prob. 35ECh. 3.4 - Prob. 36ECh. 3.4 - Prob. 37ECh. 3.4 - Prob. 38ECh. 3.4 - Prob. 39ECh. 3.4 - Prob. 40ECh. 3.4 - Prob. 41ECh. 3.4 - Prob. 42ECh. 3.4 - Prob. 43ECh. 3.4 - Prob. 44ECh. 3.4 - Prob. 45ECh. 3.4 - Prob. 46ECh. 3.4 - Prob. 47ECh. 3.4 - Prob. 48ECh. 3.4 - Prob. 49ECh. 3.4 - Prob. 50ECh. 3.4 - Prob. 51ECh. 3.4 - Prob. 52ECh. 3.4 - Prob. 53ECh. 3.4 - Prob. 54ECh. 3.4 - Prob. 55ECh. 3.4 - Prob. 56ECh. 3.4 - Prob. 57ECh. 3.4 - Prob. 58ECh. 3.4 - Prob. 59ECh. 3.4 - Prob. 60ECh. 3.4 - Prob. 61ECh. 3.4 - Prob. 62ECh. 3.4 - Prob. 63ECh. 3.4 - Prob. 64ECh. 3.4 - Prob. 65ECh. 3.4 - Prob. 66ECh. 3.4 - Prob. 67ECh. 3.4 - Prob. 68ECh. 3.4 - Prob. 69ECh. 3.4 - Prob. 70ECh. 3.4 - Prob. 71ECh. 3.4 - Prob. 72ECh. 3.4 - Prob. 73ECh. 3.4 - Prob. 74ECh. 3.4 - Prob. 75ECh. 3.4 - Prob. 76ECh. 3.4 - Prob. 77ECh. 3.4 - Prob. 78ECh. 3.4 - Prob. 79ECh. 3.4 - Prob. 80ECh. 3.4 - Prob. 81ECh. 3.4 - Prob. 82ECh. 3.4 - Prob. 83ECh. 3.4 - Prob. 84ECh. 3.4 - Prob. 85ECh. 3.4 - Prob. 86ECh. 3.4 - Prob. 87ECh. 3.4 - Prob. 88ECh. 3.4 - Prob. 89ECh. 3.4 - Prob. 90ECh. 3.4 - Prob. 91ECh. 3.4 - Prob. 92ECh. 3.4 - Prob. 93ECh. 3.4 - Prob. 94ECh. 3.4 - Prob. 95ECh. 3.4 - Prob. 96ECh. 3.4 - Prob. 97ECh. 3.4 - Prob. 98ECh. 3.4 - Prob. 99ECh. 3.4 - Prob. 100ECh. 3.4 - Possible Rational Zeros List all possible rational...Ch. 3.4 - Prob. 102ECh. 3.4 - Prob. 103ECh. 3.4 - Prob. 104ECh. 3.4 - Prob. 105ECh. 3.4 - Prob. 106ECh. 3.4 - Possible Rational Zeros A polynomial function P...Ch. 3.4 - Possible Rational Zeros A polynomial function P...Ch. 3.5 - Prob. 1ECh. 3.5 - Prob. 2ECh. 3.5 - Prob. 3ECh. 3.5 - Prob. 4ECh. 3.5 - Prob. 5ECh. 3.5 - Prob. 6ECh. 3.5 - Prob. 7ECh. 3.5 - Prob. 8ECh. 3.5 - Prob. 9ECh. 3.5 - Prob. 10ECh. 3.5 - Prob. 11ECh. 3.5 - Prob. 12ECh. 3.5 - Prob. 13ECh. 3.5 - Prob. 14ECh. 3.5 - Prob. 15ECh. 3.5 - Prob. 16ECh. 3.5 - Prob. 17ECh. 3.5 - Prob. 18ECh. 3.5 - Prob. 19ECh. 3.5 - Prob. 20ECh. 3.5 - Prob. 21ECh. 3.5 - Prob. 22ECh. 3.5 - Prob. 23ECh. 3.5 - Prob. 24ECh. 3.5 - Prob. 25ECh. 3.5 - Prob. 26ECh. 3.5 - Prob. 27ECh. 3.5 - Prob. 28ECh. 3.5 - Prob. 29ECh. 3.5 - Prob. 30ECh. 3.5 - Prob. 31ECh. 3.5 - Prob. 32ECh. 3.5 - Prob. 33ECh. 3.5 - Prob. 34ECh. 3.5 - Prob. 35ECh. 3.5 - Prob. 36ECh. 3.5 - Prob. 37ECh. 3.5 - Prob. 38ECh. 3.5 - Prob. 39ECh. 3.5 - Prob. 40ECh. 3.5 - Prob. 41ECh. 3.5 - Prob. 42ECh. 3.5 - Prob. 43ECh. 3.5 - Prob. 44ECh. 3.5 - Prob. 45ECh. 3.5 - Prob. 46ECh. 3.5 - Prob. 47ECh. 3.5 - Prob. 48ECh. 3.5 - Prob. 49ECh. 3.5 - Prob. 50ECh. 3.5 - Prob. 51ECh. 3.5 - Prob. 52ECh. 3.5 - Prob. 53ECh. 3.5 - Prob. 54ECh. 3.5 - Prob. 55ECh. 3.5 - Prob. 56ECh. 3.5 - Prob. 57ECh. 3.5 - Prob. 58ECh. 3.5 - Prob. 59ECh. 3.5 - Prob. 60ECh. 3.5 - Prob. 61ECh. 3.5 - Prob. 62ECh. 3.5 - Prob. 63ECh. 3.5 - Prob. 64ECh. 3.5 - Prob. 65ECh. 3.5 - Prob. 66ECh. 3.5 - Prob. 67ECh. 3.5 - Prob. 68ECh. 3.5 - Prob. 69ECh. 3.5 - Prob. 70ECh. 3.5 - Prob. 71ECh. 3.5 - Prob. 72ECh. 3.5 - Prob. 73ECh. 3.5 - Prob. 74ECh. 3.5 - Prob. 75ECh. 3.5 - Prob. 76ECh. 3.5 - Prob. 77ECh. 3.5 - Prob. 78ECh. 3.5 - Prob. 79ECh. 3.5 - Prob. 80ECh. 3.5 - Prob. 81ECh. 3.5 - Prob. 82ECh. 3.6 - Prob. 1ECh. 3.6 - (a) If a is a zero of the polynomial P, then...Ch. 3.6 - A polynomial of degree n 1 has exactly ________...Ch. 3.6 - Prob. 4ECh. 3.6 - Prob. 5ECh. 3.6 - Prob. 6ECh. 3.6 - Prob. 7ECh. 3.6 - Prob. 8ECh. 3.6 - Prob. 9ECh. 3.6 - Prob. 10ECh. 3.6 - Prob. 11ECh. 3.6 - Prob. 12ECh. 3.6 - Prob. 13ECh. 3.6 - Prob. 14ECh. 3.6 - Prob. 15ECh. 3.6 - Prob. 16ECh. 3.6 - Prob. 17ECh. 3.6 - Prob. 18ECh. 3.6 - Prob. 19ECh. 3.6 - Prob. 20ECh. 3.6 - Prob. 21ECh. 3.6 - Prob. 22ECh. 3.6 - Prob. 23ECh. 3.6 - Prob. 24ECh. 3.6 - Prob. 25ECh. 3.6 - Prob. 26ECh. 3.6 - Prob. 27ECh. 3.6 - Prob. 28ECh. 3.6 - Prob. 29ECh. 3.6 - Prob. 30ECh. 3.6 - Prob. 31ECh. 3.6 - Prob. 32ECh. 3.6 - Prob. 33ECh. 3.6 - Prob. 34ECh. 3.6 - Prob. 35ECh. 3.6 - Prob. 36ECh. 3.6 - Prob. 37ECh. 3.6 - Prob. 38ECh. 3.6 - Prob. 39ECh. 3.6 - Prob. 40ECh. 3.6 - Prob. 41ECh. 3.6 - Prob. 42ECh. 3.6 - Prob. 43ECh. 3.6 - Prob. 44ECh. 3.6 - Prob. 45ECh. 3.6 - Prob. 46ECh. 3.6 - Prob. 47ECh. 3.6 - Prob. 48ECh. 3.6 - Prob. 49ECh. 3.6 - Prob. 50ECh. 3.6 - Prob. 51ECh. 3.6 - Prob. 52ECh. 3.6 - Prob. 53ECh. 3.6 - Prob. 54ECh. 3.6 - Prob. 55ECh. 3.6 - Prob. 56ECh. 3.6 - Prob. 57ECh. 3.6 - Prob. 58ECh. 3.6 - Prob. 59ECh. 3.6 - Prob. 60ECh. 3.6 - Prob. 61ECh. 3.6 - Prob. 62ECh. 3.6 - Prob. 63ECh. 3.6 - Prob. 64ECh. 3.6 - Prob. 65ECh. 3.6 - Prob. 66ECh. 3.6 - Prob. 67ECh. 3.6 - Prob. 68ECh. 3.6 - Prob. 69ECh. 3.6 - Prob. 70ECh. 3.6 - Prob. 71ECh. 3.6 - Prob. 72ECh. 3.6 - Prob. 73ECh. 3.6 - Prob. 74ECh. 3.7 - If the rational function y = r(x) has the vertical...Ch. 3.7 - If the rational function y = r(x) has the...Ch. 3.7 - Prob. 3ECh. 3.7 - Prob. 4ECh. 3.7 - Prob. 5ECh. 3.7 - Prob. 6ECh. 3.7 - Prob. 7ECh. 3.7 - Prob. 8ECh. 3.7 - Prob. 9ECh. 3.7 - Prob. 10ECh. 3.7 - Prob. 11ECh. 3.7 - Prob. 12ECh. 3.7 - Prob. 13ECh. 3.7 - Prob. 14ECh. 3.7 - Prob. 15ECh. 3.7 - Prob. 16ECh. 3.7 - Prob. 17ECh. 3.7 - Prob. 18ECh. 3.7 - Prob. 19ECh. 3.7 - Prob. 20ECh. 3.7 - Prob. 21ECh. 3.7 - Prob. 22ECh. 3.7 - Prob. 23ECh. 3.7 - Prob. 24ECh. 3.7 - Prob. 25ECh. 3.7 - Prob. 26ECh. 3.7 - Prob. 27ECh. 3.7 - Prob. 28ECh. 3.7 - Prob. 29ECh. 3.7 - Prob. 30ECh. 3.7 - Prob. 31ECh. 3.7 - Prob. 32ECh. 3.7 - Prob. 33ECh. 3.7 - Prob. 34ECh. 3.7 - Prob. 35ECh. 3.7 - Prob. 36ECh. 3.7 - Prob. 37ECh. 3.7 - Prob. 38ECh. 3.7 - Prob. 39ECh. 3.7 - Prob. 40ECh. 3.7 - Prob. 41ECh. 3.7 - Prob. 42ECh. 3.7 - Prob. 43ECh. 3.7 - Prob. 44ECh. 3.7 - Prob. 45ECh. 3.7 - Prob. 46ECh. 3.7 - Prob. 47ECh. 3.7 - Prob. 48ECh. 3.7 - Prob. 49ECh. 3.7 - Prob. 50ECh. 3.7 - Prob. 51ECh. 3.7 - Prob. 52ECh. 3.7 - Prob. 53ECh. 3.7 - Prob. 54ECh. 3.7 - Prob. 55ECh. 3.7 - Prob. 56ECh. 3.7 - Prob. 57ECh. 3.7 - Prob. 58ECh. 3.7 - Prob. 59ECh. 3.7 - Prob. 60ECh. 3.7 - Prob. 61ECh. 3.7 - Prob. 62ECh. 3.7 - Prob. 63ECh. 3.7 - Prob. 64ECh. 3.7 - Prob. 65ECh. 3.7 - Prob. 66ECh. 3.7 - Prob. 67ECh. 3.7 - Prob. 68ECh. 3.7 - Prob. 69ECh. 3.7 - Prob. 70ECh. 3.7 - Prob. 71ECh. 3.7 - Prob. 72ECh. 3.7 - Prob. 73ECh. 3.7 - Prob. 74ECh. 3.7 - Prob. 75ECh. 3.7 - Prob. 76ECh. 3.7 - Prob. 77ECh. 3.7 - Prob. 78ECh. 3.7 - Prob. 79ECh. 3.7 - Prob. 80ECh. 3.7 - Prob. 81ECh. 3.7 - Prob. 82ECh. 3.7 - Prob. 83ECh. 3.7 - Drug Concentration After a certain drug is...Ch. 3.7 - Drug Concentration A drug is administered to a...Ch. 3.7 - Flight of a Rocket Suppose a rocket is fired...Ch. 3.7 - The Doppler Effect As a train moves toward an...Ch. 3.7 - Prob. 88ECh. 3.7 - Prob. 89ECh. 3.7 - Prob. 90ECh. 3.7 - Prob. 91ECh. 3.7 - Prob. 92ECh. 3 - Prob. 1RCCCh. 3 - Prob. 2RCCCh. 3 - Prob. 3RCCCh. 3 - Prob. 4RCCCh. 3 - Prob. 5RCCCh. 3 - Prob. 6RCCCh. 3 - Prob. 7RCCCh. 3 - Prob. 8RCCCh. 3 - Prob. 9RCCCh. 3 - Prob. 10RCCCh. 3 - Prob. 11RCCCh. 3 - Prob. 12RCCCh. 3 - Prob. 13RCCCh. 3 - Prob. 1RECh. 3 - Prob. 2RECh. 3 - Prob. 3RECh. 3 - Prob. 4RECh. 3 - Prob. 5RECh. 3 - Prob. 6RECh. 3 - Prob. 7RECh. 3 - Prob. 8RECh. 3 - Prob. 9RECh. 3 - Prob. 10RECh. 3 - Prob. 11RECh. 3 - Prob. 12RECh. 3 - Prob. 13RECh. 3 - Prob. 14RECh. 3 - Prob. 15RECh. 3 - Prob. 16RECh. 3 - Prob. 17RECh. 3 - Prob. 18RECh. 3 - Prob. 19RECh. 3 - Prob. 20RECh. 3 - Prob. 21RECh. 3 - Prob. 22RECh. 3 - Prob. 23RECh. 3 - Prob. 24RECh. 3 - Prob. 25RECh. 3 - Prob. 26RECh. 3 - Prob. 27RECh. 3 - Prob. 28RECh. 3 - Prob. 29RECh. 3 - Prob. 30RECh. 3 - Prob. 31RECh. 3 - Prob. 32RECh. 3 - Prob. 33RECh. 3 - Prob. 34RECh. 3 - Prob. 35RECh. 3 - Prob. 36RECh. 3 - Prob. 37RECh. 3 - Prob. 38RECh. 3 - Prob. 39RECh. 3 - Prob. 40RECh. 3 - Prob. 41RECh. 3 - Prob. 42RECh. 3 - Prob. 43RECh. 3 - Prob. 44RECh. 3 - Prob. 45RECh. 3 - Prob. 46RECh. 3 - Prob. 47RECh. 3 - Prob. 48RECh. 3 - Prob. 49RECh. 3 - Prob. 50RECh. 3 - Prob. 51RECh. 3 - Prob. 52RECh. 3 - Prob. 53RECh. 3 - Prob. 54RECh. 3 - Prob. 55RECh. 3 - Prob. 56RECh. 3 - Prob. 57RECh. 3 - Prob. 58RECh. 3 - Prob. 59RECh. 3 - Prob. 60RECh. 3 - Prob. 61RECh. 3 - Prob. 62RECh. 3 - Prob. 63RECh. 3 - Prob. 64RECh. 3 - Prob. 65RECh. 3 - Prob. 66RECh. 3 - Prob. 67RECh. 3 - Prob. 68RECh. 3 - Prob. 69RECh. 3 - Prob. 70RECh. 3 - Prob. 71RECh. 3 - Prob. 72RECh. 3 - Prob. 73RECh. 3 - Prob. 74RECh. 3 - Prob. 75RECh. 3 - Prob. 76RECh. 3 - Prob. 77RECh. 3 - Prob. 78RECh. 3 - Prob. 79RECh. 3 - Prob. 80RECh. 3 - Prob. 81RECh. 3 - Prob. 82RECh. 3 - Prob. 83RECh. 3 - Prob. 84RECh. 3 - Prob. 85RECh. 3 - Prob. 86RECh. 3 - Express the quadratic function f(x) = x2 x 6 in...Ch. 3 - Find the maximum or minimum value of the quadratic...Ch. 3 - A cannonball fired out to sea from a shore battery...Ch. 3 - Graph the polynomial P(x) = (x + 2)3 + 27, showing...Ch. 3 - (a) Use synthetic division to find the quotient...Ch. 3 - Let P(x) = 2x3 5x2 4x + 3. (a) List all possible...Ch. 3 - Prob. 7TCh. 3 - Find all real and complex zeros of P(x) = x3 x2 ...Ch. 3 - Find the complete factorization of P(x) = x4 2x3...Ch. 3 - Find a fourth-degree polynomial with integer...Ch. 3 - Let P(x) = 2x4 7x3 + x2 18x + 3. (a) Use...Ch. 3 - Prob. 12TCh. 3 - Prob. 1PCh. 3 - Prob. 2PCh. 3 - How Fast Can You List Your Favorite Things? If you...Ch. 3 - Prob. 4PCh. 3 - Height of a Baseball A baseball is thrown upward,...Ch. 3 - Torricelli's Law Water in a tank will flow out of...
Knowledge Booster
Learn more about
Need a deep-dive on the concept behind this application? Look no further. Learn more about this topic, calculus and related others by exploring similar questions and additional content below.Similar questions
- Solve please thanks!arrow_forwardSolve please and thank youarrow_forwardAccording to Newton's law of universal gravitation, the force F between two bodies of constant mass GmM m and M is given by the formula F = , where G is the gravitational constant and d is the d² distance between the bodies. a. Suppose that G, m, and M are constants. Find the rate of change of force F with respect to distance d. F' (d) 2GmM b. Find the rate of change of force F with gravitational constant G = 6.67 × 10-¹¹ Nm²/kg², on two bodies 5 meters apart, each with a mass of 250 kilograms. Answer in scientific notation, rounding to 2 decimal places. -6.67x10 N/m syntax incomplete.arrow_forward
- Solve please and thank youarrow_forwardmv2 The centripetal force of an object of mass m is given by F (r) = rotation and r is the distance from the center of rotation. ' where v is the speed of r a. Find the rate of change of centripetal force with respect to the distance from the center of rotation. F(r) b. Find the rate of change of centripetal force of an object with mass 500 kilograms, velocity of 13.86 m/s, and a distance from the center of rotation of 300 meters. Round to 2 decimal places. N/m (or kg/s²) F' (300)arrow_forwardSolve work shown please and thanks!arrow_forward
- Given the following graph of the function y = f(x) and n = = 6, answer the following questions about the area under the curve from x graph to enlarge it.) 1 (Round your answer to within two decimal places if necessary, but do not round until your final computation.) a. Use the Trapezoidal Rule to estimate the area. Estimate: T6 G b. Use Simpson's Rule to estimate the area. Estimate: S6 - ID = 0 to x = 6. (Click on aarrow_forward"Solve the following differential equation using the Operator Method and the Determinant Method:" Solve by dr no ai """'+3y"" + 3y+y=arrow_forward(4,4) M -4 2 2 -4 (-4,-4) 4 8 10 12 (8,-4) (12,-4) Graph of f The figure shows the graph of a piecewise-linear function f. For −4≤x≤12, the function g is x defined by g(x) = √ƒ (t)dt . . Find the value of g(6). Find the value of g'(6). |arrow_forward
- PREVIOUS ANSWERS ASK YOUR TEACHER PRACTICE ANOTHER Find the derivative of the function. f'(x) = X x + √3x f(x) = 3x-5 (3√√3x+11√√x+5√3 2√√x (3x-5)² Need Help? Read It SUBMIT ANSWERarrow_forwardPREVIOUS ANSWERS ASK YOUR TEACHER PRACTICE A Find the derivative of the function and evaluate f'(x) at the given val f(x) = (√√√x + 3x) (x3/2 - x); x = 1 f'(x) = 9x 412 (12x (13) 2 - 4x-3√√√x f'(1) = 2 Need Help? Read It Watch It SUBMIT ANSWERarrow_forwardConsider the following functions. g(x) = x + √3x h(x) = 3x-5 x + √3x f(x) = = 3x-5 Find the derivative of each function. g'(x) h'(x) = = f'(x) = 3 = +1 2√3x 3 (3√3x + 10√√x +5√√√3 2√√x (3x-5)² Need Help? Read It SUBMIT ANSWERarrow_forward
arrow_back_ios
SEE MORE QUESTIONS
arrow_forward_ios
Recommended textbooks for you
Calculus: Early TranscendentalsCalculusISBN:9781285741550Author:James StewartPublisher:Cengage Learning
Thomas' Calculus (14th Edition)CalculusISBN:9780134438986Author:Joel R. Hass, Christopher E. Heil, Maurice D. WeirPublisher:PEARSON
Calculus: Early Transcendentals (3rd Edition)CalculusISBN:9780134763644Author:William L. Briggs, Lyle Cochran, Bernard Gillett, Eric SchulzPublisher:PEARSON
Calculus: Early TranscendentalsCalculusISBN:9781319050740Author:Jon Rogawski, Colin Adams, Robert FranzosaPublisher:W. H. Freeman
Calculus: Early Transcendental FunctionsCalculusISBN:9781337552516Author:Ron Larson, Bruce H. EdwardsPublisher:Cengage Learning
Calculus: Early Transcendentals
Calculus
ISBN:9781285741550
Author:James Stewart
Publisher:Cengage Learning
Thomas' Calculus (14th Edition)
Calculus
ISBN:9780134438986
Author:Joel R. Hass, Christopher E. Heil, Maurice D. Weir
Publisher:PEARSON
Calculus: Early Transcendentals (3rd Edition)
Calculus
ISBN:9780134763644
Author:William L. Briggs, Lyle Cochran, Bernard Gillett, Eric Schulz
Publisher:PEARSON
Calculus: Early Transcendentals
Calculus
ISBN:9781319050740
Author:Jon Rogawski, Colin Adams, Robert Franzosa
Publisher:W. H. Freeman
Calculus: Early Transcendental Functions
Calculus
ISBN:9781337552516
Author:Ron Larson, Bruce H. Edwards
Publisher:Cengage Learning
08 - Conic Sections - Hyperbolas, Part 1 (Graphing, Asymptotes, Hyperbola Equation, Focus); Author: Math and Science;https://www.youtube.com/watch?v=Ryj0DcdGPXo;License: Standard YouTube License, CC-BY