
Concept explainers
In Figure P36.10 (not to scale), let L = 1.20 m and d = 0.120 mm and assume the slit system is illuminated with monochromatic 500-nm light. Calculate the phase difference between the two wave fronts arriving at P when (a) θ = 0.500° and (b) y = 5.00 mm. (c) What is the value of θ for which the phase difference is 0.333 rad? (d) What is the value of θ for which the path difference is λ/4?
Figure P36.10
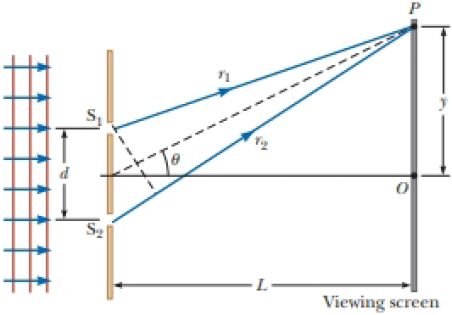
(a)
Answer to Problem 37.18P
Explanation of Solution
Given info: The separation between the slits is
The given diagram is shown below.
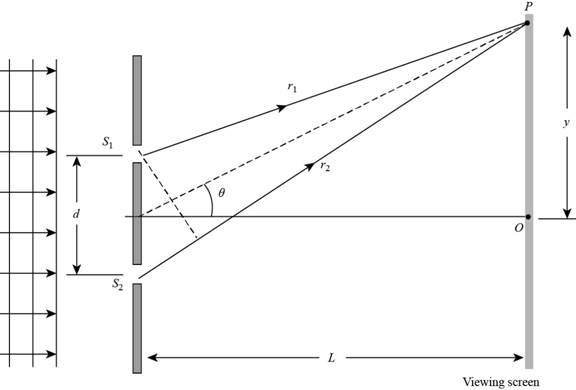
Figure 1
The formula to calculate the phase difference is,
Here,
Substitute
Conclusion:
Therefore, the phase difference between the two waves fronts arriving at
(b)
Answer to Problem 37.18P
Explanation of Solution
Given info: The separation between the slits is
The formula to calculate the phase difference is,
Here,
From the right angle triangle
Here,
Substitute
Substitute
Conclusion:
Therefore, the phase difference between the two waves fronts arriving at
(c)
Answer to Problem 37.18P
Explanation of Solution
Given info: The separation between the slits is
The formula to calculate the phase difference is,
Here,
Rearrange the above formula to find
Substitute
Conclusion:
Therefore, the value of
(d)
Answer to Problem 37.18P
Explanation of Solution
Given info: The separation between the slits is
The formula to calculate the phase difference is,
Here,
The path difference is
Substitute
Rearrange the equation (1) to find
Substitute
Conclusion:
Therefore, the value of
Want to see more full solutions like this?
Chapter 37 Solutions
Physics for Scientists and Engineers, Technology Update (No access codes included)
- Please solve this problem correctly please and be sure to provide explanation on each step so I can understand what's been done thank you. (preferrably type out everything)arrow_forwardUse a calculation to determine how far the fishing boat is from the water level .Determine distance Yarrow_forwardNo chatgpt pls will upvote Already got wrong chatgpt answerarrow_forward
- 2. 1. Tube Rating Charts Name: Directions: For the given information state if the technique is safe or unsafe and why. 60 Hertz Stator Operation Effective Focal Spot Size- 0.6 mm Peak Kilovolts MA 2 150 140 130 120 110 100 90 80 70 2501 60 50 40 30 .01 .02 .04.06 .1 .2 .4.6 1 8 10 Maximum Exposure Time In Seconds Is an exposure of 80 kVp, 0.1 second and 200 mA within the limits of the single phase, 0.6 mm focal spot tube rating chart above? Is an exposure of 100 kVp, 0.9 second and 150 mA within the limits of the single phase, 0.6 mm focal spot tube rating chart above?arrow_forwardQ: You have a CO2 laser resonator (λ = 10.6 μm). It has two curved mirrors with R₁=10m, R2= 8m, and mirror separation /= 5m. Find: R2-10 m tl Z-O 12 R1-8 m 1. Confocal parameter. b= 21w2/2 =√1 (R1-1)(R2-1)(R1+R2-21)/R1+R2-21) 2. Beam waist at t₁ & t2- 3. Waist radius (wo). 4. 5. The radius of the laser beam outside the resonator and about 0.5m from R₂- Divergence angle. 6. Radius of curvature for phase front on the mirrors R₁ & R2-arrow_forwardNo chatgpt pls will upvotearrow_forward
 Principles of Physics: A Calculus-Based TextPhysicsISBN:9781133104261Author:Raymond A. Serway, John W. JewettPublisher:Cengage Learning
Principles of Physics: A Calculus-Based TextPhysicsISBN:9781133104261Author:Raymond A. Serway, John W. JewettPublisher:Cengage Learning Physics for Scientists and Engineers: Foundations...PhysicsISBN:9781133939146Author:Katz, Debora M.Publisher:Cengage Learning
Physics for Scientists and Engineers: Foundations...PhysicsISBN:9781133939146Author:Katz, Debora M.Publisher:Cengage Learning Physics for Scientists and Engineers with Modern ...PhysicsISBN:9781337553292Author:Raymond A. Serway, John W. JewettPublisher:Cengage Learning
Physics for Scientists and Engineers with Modern ...PhysicsISBN:9781337553292Author:Raymond A. Serway, John W. JewettPublisher:Cengage Learning Physics for Scientists and EngineersPhysicsISBN:9781337553278Author:Raymond A. Serway, John W. JewettPublisher:Cengage Learning
Physics for Scientists and EngineersPhysicsISBN:9781337553278Author:Raymond A. Serway, John W. JewettPublisher:Cengage Learning Glencoe Physics: Principles and Problems, Student...PhysicsISBN:9780078807213Author:Paul W. ZitzewitzPublisher:Glencoe/McGraw-Hill
Glencoe Physics: Principles and Problems, Student...PhysicsISBN:9780078807213Author:Paul W. ZitzewitzPublisher:Glencoe/McGraw-Hill University Physics Volume 3PhysicsISBN:9781938168185Author:William Moebs, Jeff SannyPublisher:OpenStax
University Physics Volume 3PhysicsISBN:9781938168185Author:William Moebs, Jeff SannyPublisher:OpenStax





