University Physics with Modern Physics Plus Mastering Physics with eText -- Access Card Package (14th Edition)
14th Edition
ISBN: 9780321982582
Author: Hugh D. Young, Roger A. Freedman
Publisher: PEARSON
expand_more
expand_more
format_list_bulleted
Concept explainers
Videos
Textbook Question
Chapter 35, Problem 35.56CP
CP Figure P35.56 shows an interferometer known as Fresnel’s biprism. The magnitude of the prism angle A is extremely small. (a) If S0 is a very narrow source slit, show that the separation of the two virtual coherent sources S1 and S2 is given by d = 2aA(n − 1), where n is the index of refraction of the material of the prism. (b) Calculate the spacing of the fringes of green light with wavelength 500 nm on a screen 2.00 m from the biprism. Take a = 0.200 m, A = 3.50 mrad, and n = 1.50.
Figure P35.56
Expert Solution & Answer
Want to see the full answer?
Check out a sample textbook solution
Students have asked these similar questions
The Michelson interferometer can be used to measure the index of refraction of a gas by placing an evacuated transparent tube in the light path along one arm of the device. Fringe shifts occur as the
gas is slowly added to the tube. Assume 580-nm light is used, the tube is 5.40 cm long, and 152 fringe shifts occur as the pressure of the gas in the tube increases to atmospheric pressure. What is
the index of refraction of the gas? Hint: The fringe shifts occur because the wavelength of the light changes inside the gas-filled tube. (Give your answer to five decimal places.)
4.0
In the double-slit arrangement of Figure P37.21, d =
0.150 mm, L = 140 cm, A = 643 nm, and y = 1.80 cm.
(a) What is the path difference d for the rays from the
two slits arriving at P? (b) Express this path difference
in terms of A. (c) Does P correspond to a maximum,
a minimum, or an intermediate condition? Give evi-
dence for your answer.
Viewing screen
One leg of a Michelson interferometer contains an evacuated cylinder of length L,
=0.30m having glass plates on each end. A gas is slowly leaked into the cylinder until
a pressure of 1 atm is reached. If 140 bright fringes pass on the screen when light of
wavelength A=440nm is used, what is n, the index of refraction of the gas? State
your answer to the nearest 0.000001 ( one part per million).
Chapter 35 Solutions
University Physics with Modern Physics Plus Mastering Physics with eText -- Access Card Package (14th Edition)
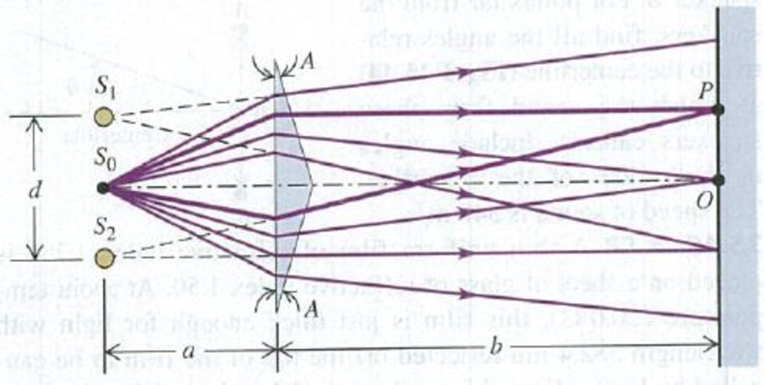
Ch. 35.1 - Consider a point in Fig. 35.3 on the positive...Ch. 35.2 - You shine a tunable laser (whose wavelength can be...Ch. 35.3 - A two-slit interference experiment uses coherent...Ch. 35.4 - A thin layer of benzene (n = 1.501) lies on top of...Ch. 35.5 - You are observing the pattern of fringes in a...Ch. 35 - A two-slit interference experiment is set up, and...Ch. 35 - Could an experiment similar to Youngs two-slit...Ch. 35 - Monochromatic coherent light passing through two...Ch. 35 - In a two-slit interference pattern on a distant...Ch. 35 - Would the headlights of a distant car form a...
Ch. 35 - The two sources S1 and S2 shown in Fig. 35.3 emit...Ch. 35 - Could the Young two-slit interference experiment...Ch. 35 - Coherent red light illuminates two narrow slits...Ch. 35 - Coherent light with wavelength falls on two...Ch. 35 - Prob. 35.10DQCh. 35 - If the monochromatic light shown in Fig. 35.5a...Ch. 35 - In using the superposition principle to calculate...Ch. 35 - Prob. 35.13DQCh. 35 - A very thin soap film (n = 1.33), whose thickness...Ch. 35 - Interference can occur in thin films. Why is it...Ch. 35 - If we shine while light on an air wedge like that...Ch. 35 - Prob. 35.17DQCh. 35 - When a thin oil film spreads out on a puddle of...Ch. 35 - Section 35.1 Interference and Coherent Sources...Ch. 35 - Two speakers that are 15.0 m apart produce...Ch. 35 - A radio transmitting station operating at a...Ch. 35 - Radio Interference. Two radio antennas A and B...Ch. 35 - Prob. 35.5ECh. 35 - Two light sources can be adjusted to emit...Ch. 35 - Section 35.2 Two-Source Interference of Light...Ch. 35 - Coherent light with wavelength 450 nm falls on a...Ch. 35 - Two slits spaced 0.450 mm apart are placed 75.0 cm...Ch. 35 - If the entire apparatus of Exercise 35.9 (slits,...Ch. 35 - Two thin parallel slits that are 0.0116 mm apart...Ch. 35 - Coherent light with wavelength 400 nm passes...Ch. 35 - Two very narrow slits are spaced 1.80 m apart and...Ch. 35 - Coherent light that contains two wavelengths. 660...Ch. 35 - Coherent light with wavelength 600 nm passes...Ch. 35 - Coherent light of frequency 6.32 1014 Hz passes...Ch. 35 - In a two-slit interference pattern, the intensity...Ch. 35 - Coherent sources A and B emit electromagnetic...Ch. 35 - Coherent light with wavelength 500 nm passes...Ch. 35 - Two slits spaced 0.260 mm apart are 0.900 m from a...Ch. 35 - Consider two antennas separated by 9.00 m that...Ch. 35 - Two slits spaced 0.0720 mm apart are 0.800 m from...Ch. 35 - What is the thinnest film of a coating with n =...Ch. 35 - Nonglare Glass. When viewing a piece of art that...Ch. 35 - Two rectangular pieces of plane glass are laid one...Ch. 35 - A place of glass 9.00 cm long is placed in contact...Ch. 35 - A uniform film of TiO2, 1036 nm thick and having...Ch. 35 - A plastic film with index of refraction 1.70 is...Ch. 35 - The walls of a soap bubble have about the same...Ch. 35 - A researcher measures the thickness of a layer of...Ch. 35 - Prob. 35.31ECh. 35 - What is the thinnest soap film (excluding the case...Ch. 35 - How far must the mirror M2 (see Fig. 35.19) of the...Ch. 35 - Jan first uses a Michelson interferometer with the...Ch. 35 - One round face of a 3.25-m, solid, cylindrical...Ch. 35 - Newtons rings are visible when a planoconvex lens...Ch. 35 - BIO Coating Eyeglass Lenses. Eyeglass lenses can...Ch. 35 - BIO Sensitive Eyes. After an eye examination, you...Ch. 35 - Two flat plates of glass with parallel faces are...Ch. 35 - In a setup similar to that of Problem 35.39, the...Ch. 35 - Suppose you illuminate two thin slits by...Ch. 35 - CP CALC A very thin sheet of brass contains two...Ch. 35 - Two radio antennas radiating in phase are located...Ch. 35 - Prob. 35.44PCh. 35 - CP A thin uniform film of refractive index 1.750...Ch. 35 - GPS Transmission. The GPS (Global Positioning...Ch. 35 - White light reflects at normal incidence from the...Ch. 35 - Laser light of wavelength 510 nm is traveling in...Ch. 35 - Red light with wavelength 700 nm is passed through...Ch. 35 - BIO Reflective Coatings and Herring. Herring and...Ch. 35 - After a laser beam passes through two thin...Ch. 35 - DATA In your summer job at an optics company, you...Ch. 35 - DATA Short-wave radio antennas A and B are...Ch. 35 - DATA In your research lab, a very thin, flat piece...Ch. 35 - CP The index of refraction of a glass rod is 1.48...Ch. 35 - CP Figure P35.56 shows an interferometer known as...Ch. 35 - INTERFERENCE AND SOUND WAVES. Interference occurs...Ch. 35 - The professor returns the apparatus to the...Ch. 35 - The professor again returns the apparatus to its...Ch. 35 - The professor once again returns the apparatus to...
Additional Science Textbook Solutions
Find more solutions based on key concepts
The Sun is approximately 6000 K at the surface and has an energy distribution that peaks at visible wavelengths...
Lecture- Tutorials for Introductory Astronomy
61. A space beacon on Planet Karma emits a pulse of light every second. Spaceman Trevor flies directly toward t...
College Physics: A Strategic Approach (4th Edition)
43. A 0.100 μg speck of dust is accelerated from rest to a speed of 0.900c by a constant 1.00 × 106N force. (a)...
College Physics (10th Edition)
26. The earth’s radius is about 4000 miles. Kampala, the capital of Uganda, and Singapore are both nearly on t...
Physics for Scientists and Engineers: A Strategic Approach, Vol. 1 (Chs 1-21) (4th Edition)
The velocity of the train relative to the ground.
College Physics: A Strategic Approach (3rd Edition)
Knowledge Booster
Learn more about
Need a deep-dive on the concept behind this application? Look no further. Learn more about this topic, physics and related others by exploring similar questions and additional content below.Similar questions
- A beam of 580-nm light passes through two closely spaced glass plates at close to normal incidence as shown in Figure P27.23. For what minimum nonzero value of the plate separation d is the transmitted light bright?arrow_forwardTable P35.80 presents data gathered by students performing a double-slit experiment. The distance between the slits is 0.0700 mm, and the distance to the screen is 2.50 m. The intensity of the central maximum is 6.50 106 W/m2. What is the intensity at y = 0.500 cm? TABLE P35.80arrow_forwardCoherent light rays of wavelength strike a pair of slits separated by distance d at an angle 1, with respect to the normal to the plane containing the slits as shown in Figure P27.14. The rays leaving the slits make an angle 2 with respect to the normal, and an interference maximum is formed by those rays on a screen that is a great distance from the slits. Show that the angle 2 is given by 2=sin1(sin1md) where m is an integer.arrow_forward
- Both sides of a uniform film that has index of refraction n and thickness d are in contact with air. For normal incidence of light, an intensity minimum is observed in the reflected light at λ2 and an intensity maximum is observed at λ1, where λ1 > λ2. (a) Assuming no intensity minima are observed between λ1 and λ2, find an expression for the integer m in Equations 27.13 and 27.14 in terms of the wavelengths λ1 and λ2. (b) Assuming n = 1.40, λ1 = 500 nm, and λ2 = 370 nm, determine the best estimate for the thickness of the film.arrow_forwardIn Figure P27.7 (not to scale), let L = 1.20 m and d = 0.120 mm and assume the slit system is illuminated with monochromatic 500-nm light. Calculate the phase difference between the two wave fronts arriving at P when (a) = 0.500 and (b) y = 5.00 mm. (c) What is the value of for which the phase difference is 0.333 rad? (d) What is the value of for which the path difference is /4?arrow_forwardCan you address a-b with the given information from the image?arrow_forward
- In the single-slit diffraction experiment of the figure, let the wavelength of the light be 541 nm, the slit width be 6.11 pm, and the viewing screen be at distance D = 3.41 m. Let a y axis extend upward along the viewing screen, with its origin at the center of the diffraction pattern. Also let Ip represent the intensity of the diffracted light at point P at y = 15.8 cm. (a) What is the ratio of Ip the intensity Im at the center of the pattern? Determine where point P is in the diffraction pattern by giving the orders of nearest (b) maximum (0 is the central maximum) and (c) minimum between which it lies. Totally destructive interference- P1 12 Po Central axis a/2 Viewing screen Incident wave Units (a) Number 2.98e-4 This answer has no units Units (b) Number This answer has no units Version 4.24.1 2.arrow_forwardThe limit to the eye’s visual acuity is related to diffraction by the pupil.D = 2.85 mmdh = 1.25 m a. What is the angle between two just-resolvable points of light for a 2.85 mm diameter pupil in radians, assuming an average wavelength of 550 nm? θmin = b. Take your result to be the practical limit for the eye. What is the greatest possible distance in km a car can be from you if you can resolve its two headlights, given they are 1.25 m apart? L= c. What is the distance between two just-resolvable points held at an arm’s length (0.800 m) from your eye in mm? da =arrow_forwardA thin sheet of transparent material has an index of refraction of 1.40 and is 15.0 µm thick. When it is inserted in the light path along one arm of an interferometer, how many fringe shifts occur in the pattern? Assume the wavelength (in a vac- uum) of the light used is 600 nm. Hint: The wavelength will change within the material.arrow_forward
- An optician is performing Young's double-slit experiment for her clients. She directs a beam of laser light to a pair of parallel slits, which are separated by 0.120 mm from each other. The portion of this light that passes through the slits goes on to form an interference pattern upon a screen, which is 4.50 meters distant. The light is characterized by a wavelength of 575 nm. (a) What is the optical path-length difference (in um) that corresponds to the third-order bright fringe on the screen? (This is the third fringe, not counting the central bright band, that one encounters moving from the center out to one side.) 1.73*10**3 um Enter a number. (b) What path-length difference (in um) corresponds to the third dark fringe that one encounters when moving out to one side of the central bright fringe? umarrow_forwardOne way to determine the index of refraction of a gas is to use an interferometer. As shown below, one of the beams of an interferometer passes through a glass container that has a length of L = 1.8 cm. Initially the glass container is a vacuum. When gas is slowly allowed into the container, a total of 6894 dark fringes move past the reference line. The laser has a wavelength of 635 nm (this is the wavelength when the light from the laser is moving through a vacuum). A.) Determine how many wavelengths will fit into the glass container when it is a vacuum. Since the light passes through the container twice, you need to determine how many wavelengths will fit into a glass container that has a length of 2L.number of wavelengths (vacuum) = B.) The number of dark fringes is the difference between the number of wavelengths that fit in the container (length of 2L) when it has gas and the number of wavelengths that fit in the container (length of 2L) when it is a vacuum. Use this knowledge to…arrow_forwardProblem 2. Suppose that a Michelson interferometer is illuminated by a source emitting a doublet of vacuum wavelengths, 21 and 22. As one mirror is moved, the fringes periodically disappear and then reappear. If a displacement Ad of the mirror causes a one-cycle variation in fringe visibility, derive an expression for Ad in terms of Aλ = 2-1. Then calculate Ad for the sodium doublet, where λ₁ = 588.995 nm and 2 = 589.592 nm.arrow_forward
arrow_back_ios
SEE MORE QUESTIONS
arrow_forward_ios
Recommended textbooks for you
Physics for Scientists and Engineers: Foundations...PhysicsISBN:9781133939146Author:Katz, Debora M.Publisher:Cengage Learning
Physics for Scientists and Engineers with Modern ...PhysicsISBN:9781337553292Author:Raymond A. Serway, John W. JewettPublisher:Cengage Learning
Principles of Physics: A Calculus-Based TextPhysicsISBN:9781133104261Author:Raymond A. Serway, John W. JewettPublisher:Cengage Learning
Physics for Scientists and Engineers: Foundations...
Physics
ISBN:9781133939146
Author:Katz, Debora M.
Publisher:Cengage Learning
Physics for Scientists and Engineers with Modern ...
Physics
ISBN:9781337553292
Author:Raymond A. Serway, John W. Jewett
Publisher:Cengage Learning
Principles of Physics: A Calculus-Based Text
Physics
ISBN:9781133104261
Author:Raymond A. Serway, John W. Jewett
Publisher:Cengage Learning
Convex and Concave Lenses; Author: Manocha Academy;https://www.youtube.com/watch?v=CJ6aB5ULqa0;License: Standard YouTube License, CC-BY