Chapter 35, Problem 35.52P

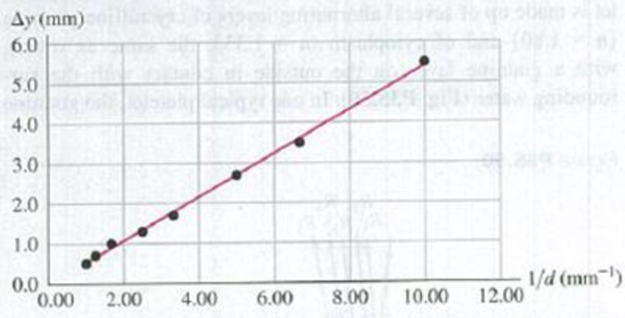
DATA In your summer job at an optics company, you are asked to measure the wavelength λ of the light that is produced by a laser. To do so, you pass the laser light through two narrow slits that are separated by a distance d. You observe the interference pattern on a screen that is 0.900 m from the slits and measure the separation Δy between adjacent bright fringes in the portion of the pattern that is near the center of the screen. Using a microscope, you measure d. But both Δy and d are small and difficult to measure accurately, so you repeat the measurements for several pairs of slits, each with a different value of d. Your results are shown in Fig. P35.52. where you have plotted Δy versus 1/d. The line in the graph is the best-fit straight line for the data. (a) Explain why the data points plotted this way fall close to a straight line. (b) Use Fig. P35.52 to calculate λ.

Figure P35.52