College Physics
1st Edition
ISBN: 9781938168048
Author: Paul Peter Urone, OpenStax, Roger Hinrichs
Publisher: OpenStax
expand_more
expand_more
format_list_bulleted
Concept explainers
Videos
Textbook Question
Chapter 34, Problem 30PE
To get an idea of how empty deep spam is on the average, perform the following calculations:
(a) Find the volume our Sun would occupy if it had an average density equal to the critical density of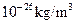 
thought necessary to halt the expansion of the universe.
(b) Find the radius of a sphere of this volume in light years.
(c) What would this radius be if the density were that of luminous matter, which is approximately 5% that of the critical density?
(d) Compare the radius found in part (c) with me 4-ly average separation of stars in the aims of the Milky Way.
Expert Solution & Answer
Want to see the full answer?
Check out a sample textbook solution
Students have asked these similar questions
Please don't use Chatgpt will upvote and give handwritten solution
Cam mechanisms are used in many machines. For example, cams open and close the valves in your car engine to admit gasoline vapor to each cylinder and to allow the escape of exhaust.
The principle is illustrated in the figure below, showing a follower rod (also called a pushrod) of mass m resting on a wedge of mass M. The sliding wedge duplicates the function of a
rotating eccentric disk on a camshaft in your car. Assume that there is no friction between the wedge and the base, between the pushrod and the wedge, or between the rod and the guide
through which it slides. When the wedge is pushed to the left by the force F, the rod moves upward and does something such as opening a valve. By varying the shape of the wedge, the
motion of the follower rod could be made quite complex, but assume that the wedge makes a constant angle of 0 = 15.0°. Suppose you want the wedge and the rod to start from rest and
move with constant acceleration, with the rod moving upward 1.00 mm in 8.00 ms. Take m…
No chatgpt pls will upvote
Chapter 34 Solutions
College Physics
Ch. 34 - Explain why it only appears that we are at the...Ch. 34 - If there is no observable edge to the universe,...Ch. 34 - If the universe is infinite, does it have a...Ch. 34 - Another known cause of red shift in light is the...Ch. 34 - If some unknown cause of red shiftsuch as light...Ch. 34 - Olbers’s paradox poses an interesting question: If...Ch. 34 - If the cosmic microwave background radiation...Ch. 34 - The decay of one type of Kmeson is cited as...Ch. 34 - Distances to local galaxies are determined by...Ch. 34 - Distances to very remote galaxies are estimated...
Ch. 34 - If the smallest meaningful time interval is...Ch. 34 - Quantum gravity, if developed, would be an...Ch. 34 - Does observed gravitational lensing correspond to...Ch. 34 - Suppose you measure the red shifts of all the...Ch. 34 - What are gravitational waves, and have they yet...Ch. 34 - Is the event horizon of a black hole the actual...Ch. 34 - Suppose black holes radiate their mass away and...Ch. 34 - Discuss the possibility that star velocities at...Ch. 34 - How does relativistic time dilation prohibit...Ch. 34 - If neutrino oscillations do occur, will they...Ch. 34 - Lacking direct evidence of WIMPs as dark matter,...Ch. 34 - Must a complex system be adaptive to be of...Ch. 34 - State a necessary condition for a System to be...Ch. 34 - What is critical temperature Tc? Do all materials...Ch. 34 - Explain how good thermal contact with liquid...Ch. 34 - Not only is liquid nitrogen a cheaper coolant than...Ch. 34 - For experimental evidence particularly of...Ch. 34 - Discuss whether you think there are limits to what...Ch. 34 - Find the approximate mass of the luminous matter...Ch. 34 - Find the approximate mass of the dark and luminous...Ch. 34 - (a) Estimate the mass of the luminous matter in...Ch. 34 - If a galaxy is 500 Mly away from us, how fast do...Ch. 34 - On average, how far away are galaxies mat are...Ch. 34 - Our solar system orbits the center of the Milky...Ch. 34 - (a) What is the approximate speed relative to us...Ch. 34 - (a) Calculate The approximate age of the universe...Ch. 34 - Assuming a circular orbit for the Sun about the...Ch. 34 - (a) What is the approximate force of gravity on a...Ch. 34 - Andromeda galaxy is the closest large galaxy and...Ch. 34 - (a) A particle and its antiparticle are at rest...Ch. 34 - The average particle energy needed to observe...Ch. 34 - The peak intensity of the CMBR occurs at a...Ch. 34 - (a) What Hubble constant corresponds to an...Ch. 34 - Show that the velocity of a star orbiting its...Ch. 34 - The core of a star collapses during a supernova,...Ch. 34 - Using data from the previous problem, find the...Ch. 34 - Distances to the nearest stars (up to 500 by away)...Ch. 34 - (a) Use the Heisenberg uncertainty principle to...Ch. 34 - Construct Your Own Problem Consider a star moving...Ch. 34 - What is the Schwarzschild radius of a blank hole...Ch. 34 - Black holes with masses smaller than muse formed...Ch. 34 - Supermassive black holes are thought to exist at...Ch. 34 - Construct Your Own Problem Consider a supermassive...Ch. 34 - The characteristic length of entities in...Ch. 34 - If the dark matter in the Milky Way were composed...Ch. 34 - The critical mass density needed to just halt the...Ch. 34 - Assume the average density of the universe is 0.1...Ch. 34 - To get an idea of how empty deep spam is on the...Ch. 34 - A section of superconducting wire carries a...
Additional Science Textbook Solutions
Find more solutions based on key concepts
Police Captain Jeffers has suffered a myocardial infarction. a. Explain to his (nonmedically oriented) family w...
Human Physiology: An Integrated Approach (8th Edition)
Match the following examples of mutagens. Column A Column B ___a. A mutagen that is incorporated into DNA in pl...
Microbiology: An Introduction
1. A cyclist goes around a level, circular track at constant speed. Do you agree or disagree with the following...
College Physics: A Strategic Approach (3rd Edition)
Define histology.
Fundamentals of Anatomy & Physiology (11th Edition)
5. When the phenotype of heterozygotes is intermediate between the phenotypes of the two homozygotes, this patt...
Biology: Life on Earth (11th Edition)
1. ___ Mitosis 2. ___ Meiosis 3. __ Homologous chromosomes 4. __ Crossing over 5. __ Cytokinesis A. Cytoplasmic...
Microbiology with Diseases by Body System (5th Edition)
Knowledge Booster
Learn more about
Need a deep-dive on the concept behind this application? Look no further. Learn more about this topic, physics and related others by exploring similar questions and additional content below.Similar questions
- No chatgpt pls will upvotearrow_forwardNo chatgpt plsarrow_forwardA rectangular current loop (a = 15.0 cm, b = 34.0 cm) is located a distance d = 10.0 cm near a long, straight wire that carries a current (Iw) of 17.0 A (see the drawing). The current in the loop is IL = 21.0 A. Determine the magnitude of the net magnetic force that acts on the loop. Solve in N. a b IL Iwarrow_forward
- Two long, straight wires are separated by distance, d = 22.0 cm. The wires carry currents of I1 = 7.50 A and I2 = 5.50 A in opposite directions, as shown in the figure. Find the magnitude of the net magnetic field at point (B). Let r₁ = 12.0 cm, r2 = 7.00 cm, and r3 = 13.0 cm. Solve in T. 12 d A √3arrow_forwardI tried to solve this question, and I had an "expert" answer it and they got it wrong. I cannot answer this questionarrow_forwardEddie Hall is the current world record holder in the deadlift, a powerlifting maneuver in which a weighted barbell is lifted from the ground to waist height, then dropped. The figure below shows a side view of the initial and final positions of the deadlift. a 0 = 55.0° Fift h22.5 cm i hy = 88.0 cm b iarrow_forward
- solve for (_) Narrow_forwardTwo boxes of fruit on a frictionless horizontal surface are connected by a light string as in the figure below, where m₁ = 11 kg and m₂ = 25 kg. A force of F = 80 N is applied to the 25-kg box. mq m1 Applies T Peaches i (a) Determine the acceleration of each box and the tension in the string. acceleration of m₁ acceleration of m₂ tension in the string m/s² m/s² N (b) Repeat the problem for the case where the coefficient of kinetic friction between each box and the surface is 0.10. acceleration of m₁ acceleration of m₂ tension in the string m/s² m/s2 Narrow_forwardAll correct but t1 and t2 from part Aarrow_forward
- Three long, straight wires are mounted on the vertices of an equilateral triangle as shown in the figure. The wires carry currents of I₁ = 3.50 A, I2 = 5.50 A, and I3 = 8.50 A. Each side of the triangle has a length of 34.0 cm, and the point (A) is located half way between (11) and (12) along one of the sides. Find the magnitude of the magnetic field at point (A). Solve in Teslas (T). I₁arrow_forwardNumber There are four charges, each with a magnitude of 2.38 μC. Two are positive and two are negative. The charges are fixed to the corners of a 0.132-m square, one to a corner, in such a way that the net force on any charge is directed toward the center of the square. Find the magnitude of the net electrostatic force experienced by any charge. ips que Mi Units estic re harrow_forwardTwo long, straight wires are separated by distance, d = 22.0 cm. The wires carry currents of I1 = 7.50 A and I2 = 5.50 A in opposite directions, as shown in the figure. Find the magnitude of the net magnetic field at point (B). Let r₁ = 12.0 cm, r2 = 7.00 cm, and r3 = 13.0 cm. Solve in T. 12 d A √3arrow_forward
arrow_back_ios
SEE MORE QUESTIONS
arrow_forward_ios
Recommended textbooks for you
Modern PhysicsPhysicsISBN:9781111794378Author:Raymond A. Serway, Clement J. Moses, Curt A. MoyerPublisher:Cengage Learning
Foundations of Astronomy (MindTap Course List)PhysicsISBN:9781337399920Author:Michael A. Seeds, Dana BackmanPublisher:Cengage Learning
Stars and Galaxies (MindTap Course List)PhysicsISBN:9781337399944Author:Michael A. SeedsPublisher:Cengage Learning
Principles of Physics: A Calculus-Based TextPhysicsISBN:9781133104261Author:Raymond A. Serway, John W. JewettPublisher:Cengage Learning
AstronomyPhysicsISBN:9781938168284Author:Andrew Fraknoi; David Morrison; Sidney C. WolffPublisher:OpenStax
Modern Physics
Physics
ISBN:9781111794378
Author:Raymond A. Serway, Clement J. Moses, Curt A. Moyer
Publisher:Cengage Learning
Foundations of Astronomy (MindTap Course List)
Physics
ISBN:9781337399920
Author:Michael A. Seeds, Dana Backman
Publisher:Cengage Learning
Stars and Galaxies (MindTap Course List)
Physics
ISBN:9781337399944
Author:Michael A. Seeds
Publisher:Cengage Learning
Principles of Physics: A Calculus-Based Text
Physics
ISBN:9781133104261
Author:Raymond A. Serway, John W. Jewett
Publisher:Cengage Learning
Astronomy
Physics
ISBN:9781938168284
Author:Andrew Fraknoi; David Morrison; Sidney C. Wolff
Publisher:OpenStax
General Relativity: The Curvature of Spacetime; Author: Professor Dave Explains;https://www.youtube.com/watch?v=R7V3koyL7Mc;License: Standard YouTube License, CC-BY