Chapter 31, Problem 50CP

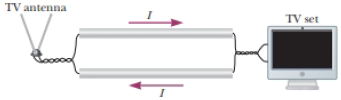
In earlier times when many households received nondigital television signals from an antenna, the lead-in wires from the antenna were often constructed in the form of two parallel wires (Fig. P31.50). The two wires carry currents of equal magnitude in opposite directions. The center-to-center separation of the wires is w, and a is their radius. Assume w is large enough compared with a that the wires carry the current uniformly distributed over their surfaces and negligible magnetic field exists inside the wires. (a) Why does this configuration of conductors have an inductance? (b) What constitutes the flux loop for this configuration? (c) Show that the inductance of a length x of this type of lead-in is

$L=\frac{{\mu }_{0}x}{\pi }\ln \left(\frac{w-a}{a}\right)$

Figure P31.50