Chapter 2.2, Problem 31E

a.

To determine

Construct the frequency distribution with approximately 5classes.

Answer to Problem 31E

The frequency distribution is,

Number of Words	Frequency
0-1,999	26
2,000-3,999	25
4,000-5,999	5
6,000-7,999	0
8,000-9,999	1
Total	57

Explanation of Solution

Calculation:

The given information is that a table representing the number of words spoken in each of these addresses.

Frequency:

The frequencies are calculated by using the tally mark and the range of the data is from 0 to 1,999.

• Based on the given information, the class intervals are 0-1,999, 2,000-3,999, 4,000-5,999, 6,000-7,999, 8,000-9,999.
• Make a tally mark for each value in the corresponding number of words spoken and continue for all values in the data.
• The number of tally marks in each class represents the frequency, f of that class.

Similarly, the frequency of remaining classes for the number of words spoken is given below:

Number of Words	Tally	Frequency
0-1,999	$\bcancel{\left|\right|\left|\right|}\bcancel{\left|\right|\left|\right|}\bcancel{\left|\right|\left|\right|}\bcancel{\left|\right|\left|\right|}\bcancel{\left|\right|\left|\right|}|$	26
2,000-3,999	$\bcancel{\left|\right|\left|\right|}\bcancel{\left|\right|\left|\right|}\bcancel{\left|\right|\left|\right|}\bcancel{\left|\right|\left|\right|}\bcancel{\left|\right|\left|\right|}$	25
4,000-5,999	$\bcancel{\left|\right|\left|\right|}$	5
6,000-7,999		0
8,000-9,999	$|$	1
Total		57

b.

To determine

Construct the frequency histogram based on the frequency distribution.

Answer to Problem 31E

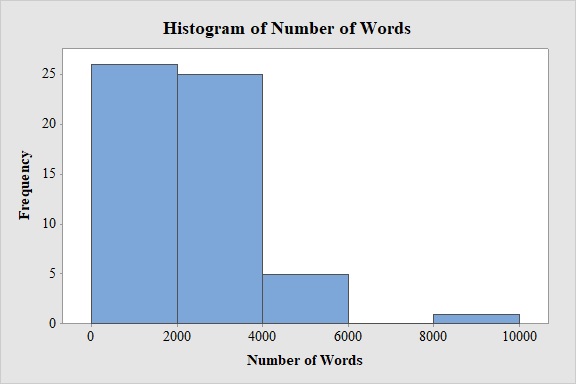
Output obtained from MINITAB software for the number of words spoken is:

Explanation of Solution

Calculation:

Frequency Histogram:

Software procedure:

• Step by step procedure to draw the relative frequency histogram for number of words spoken using MINITAB software.
• Choose Graph > Histogram.
• Choose Simple.
• Click OK.
• In Graph variables, enter the column of Number of Words.
• In Scale, Choose Y-scale Type as Frequency.
• Click OK.
• Select Edit Scale, Enter 0, 2,000, 4,000, 6,000, 8,000, 10,000 in Positions of ticks.
• In Binning, Under Interval Type select Cutpoint and under Interval Definition select Number of intervals as 5 and Cutpoint positions as 0, 2,000, 4,000, 6,000, 8,000, 10,000.
• In Labels, Enter 0, 2,000, 4,000, 6,000, 8,000, 10,000 in Specified.
• Click OK.

Observation:

From the bar graph, it can be seen that maximum number of words spoken are in the interval 0-2,000.

c.

To determine

Construct a relative frequency distribution for the data.

Answer to Problem 31E

The relative frequency distribution for the data is:

Number of Words	Relative frequency
0-1,999	0.456
2,000-3,999	0.439
4,000-5,999	0.088
6,000-7,999	0.000
8,000-9,999	0.018

Explanation of Solution

Calculation:

Relative frequency:

The general formula for the relative frequency is,

$\text{Relative}\text{Frequency = }\frac{\text{Frequency}}{\text{Total frequency}}$

Therefore,

$\begin{array}{c}\text{Relative}\text{Frequency}\text{for the class 0-1,999}=\frac{26}{57}\\ =0.456\end{array}$

Similarly, the relative frequencies for the remaining number of words spoken are obtained below:

Number of Words	Frequency	Relative frequency
0-1,999	26	$\frac{26}{57}=0.456$
2,000-3,999	25	$\frac{25}{57}=0.439$
4,000-5,999	5	$\frac{5}{57}=0.088$
6,000-7,999	0	$\frac{0}{57}=0.000$
8,000-9,999	1	$\frac{1}{57}=0.018$

d.

To determine

Construct the relative frequency histogram based on the frequency distribution.

Answer to Problem 31E

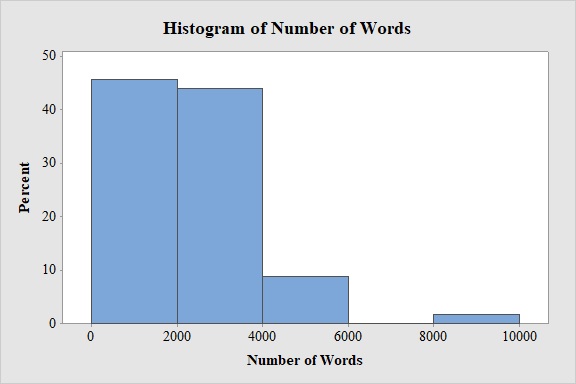
Output obtained from MINITAB software for the number of words spoken is:

Explanation of Solution

Calculation:

Relative Frequency Histogram:

Software procedure:

• Step by step procedure to draw the relative frequency histogram for the number of words spoken using MINITAB software.
• Choose Graph > Histogram.
• Choose Simple.
• Click OK.
• In Graph variables, enter the column of Number of Words.
• In Scale, Choose Y-scale Type as Percent.
• Click OK.
• Select Edit Scale, Enter 0, 2,000, 4,000, 6,000, 8,000, 10,000 in Positions of ticks.
• In Binning, Under Interval Type select Cutpoint and under Interval Definition select Number of intervals as 5 and Cutpoint positions as 0, 2,000, 4,000, 6,000, 8,000, 10,000.
• In Labels, Enter 0, 2,000, 4,000, 6,000, 8,000, 10,000 in Specified.
• Click OK.

Observation:

From the bar graph, it can be seen that maximum number of words spoken is in the interval 0-2,000.

e.

To determine

Check whether the histograms are skewed to the left, skewed to the right or approximately symmetric.

Answer to Problem 31E

The histogram is skewed to the right.

Explanation of Solution

From the given histogram, the right hand tail is larger than the left hand tail from the maximum frequency value. Hence, the shape of the distribution is right skewed.

f.

To determine

Construct the frequency distribution with approximately 9classes.

Answer to Problem 31E

The frequency distribution is,

Number of Words	Frequency
0-999	4
1,000-1,999	22
2,000-2,999	18
3,000-3,999	7
4,000-4,999	4
5,000-5,999	1
6,000-6,999	0
7,000-7,999	0
8,000-8,999	1
Total	57

Explanation of Solution

Calculation:

Frequency:

The frequencies are calculated by using the tally mark and the range of the data is from 0 to 8,999.

• Based on the given information, the class intervals are 0-999, 1,000-1,999, 2,000-2,999, 3,000-3,999, 4,000-4,999, 5,000-5,999, 6,000-6,999, 7,000-7,999, 8,000-8,999.
• Make a tally mark for each value in the corresponding number of words spoken and continue for all values in the data.
• The number of tally marks in each class represents the frequency, f of that class.

Similarly, the frequency of remaining classes for the number of words spoken is given below:

Number of Words	Tally	Frequency
0-999	$\left|\right|\left|\right|$	4
1,000-1,999	$\bcancel{\left|\right|\left|\right|}\bcancel{\left|\right|\left|\right|}\bcancel{\left|\right|\left|\right|}\bcancel{\left|\right|\left|\right|}\left|\right|$	22
2,000-2,999	$\bcancel{\left|\right|\left|\right|}\bcancel{\left|\right|\left|\right|}\bcancel{\left|\right|\left|\right|}\left|\right||$	18
3,000-3,999	$\bcancel{\left|\right|\left|\right|}\left|\right|$	7
4,000-4,999	$\left|\right|\left|\right|$	4
5,000-5,999	$|$	1
6,000-6,999		0
7,000-7,999		0
8,000-8,999	$|$	1
Total		57

g.

To determine

Repeat parts (b) to (d), using the frequency distribution constructed in part (f).

Answer to Problem 31E

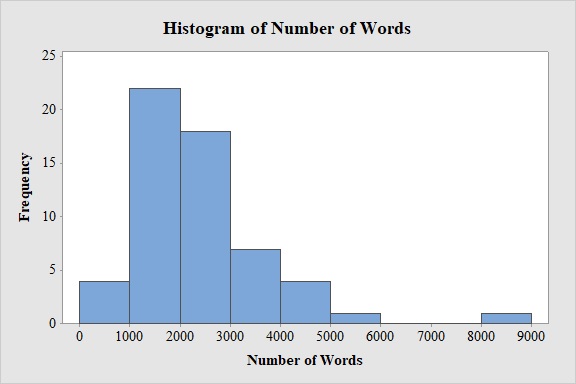
Output obtained from MINITAB software for the number of words spoken is:

The relative frequency distribution for the data is:

Number of Words	Relative frequency
0-999	0.070
1,000-1,999	0.386
2,000-2,999	0.316
3,000-3,999	0.123
4,000-4,999	0.070
5,000-5,999	0.018
6,000-6,999	0.000
7,000-7,999	0.000
8,000-8,999	0.018

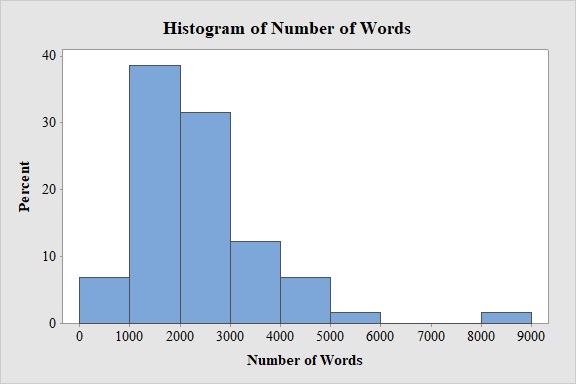
Output obtained from MINITAB software for the number of words spoken is:

Explanation of Solution

Calculation:

Frequency Histogram:

Software procedure:

• Step by step procedure to draw the relative frequency histogram for the number of words spoken using MINITAB software.
• Choose Graph > Histogram.
• Choose Simple.
• Click OK.
• In Graph variables, enter the column of Number of Words.
• In Scale, Choose Y-scale Type as Frequency.
• Click OK.
• Select Edit Scale, Enter 0, 1,000, 2,000, 3,000, 4,000, 5,000, 6,000, 7,000, 8,000, 90,00 in Positions of ticks.
• In Binning, Under Interval Type select Cutpoint and under Interval Definition select Number of intervals as 9 and Cutpoint positions as 0, 1,000, 2,000, 3,000, 4,000, 5,000, 6,000, 7,000, 8,000, 9,000.
• In Labels, Enter 0, 1,000, 2,000, 3,000, 4,000, 5,000, 6,000, 7,000, 8,000, 9,000 in Specified.
• Click OK.

Observation:

From the bar graph, it can be seen that maximum number of words spoken is in the interval 1,000-2,000.

Relative frequency:

$\begin{array}{c}\text{Relative}\text{Frequency}\text{for the class 0-999}=\frac{4}{57}\\ =0.070\end{array}$

Similarly, the relative frequencies for the remaining number of words spoken are obtained below:

Number of Words	Frequency	Relative frequency
0-999	4	$\frac{4}{57}=0.070$
1,000-1,999	22	$\frac{22}{57}=0.386$
2,000-2,999	18	$\frac{18}{57}=0.316$
3,000-3,999	7	$\frac{7}{57}=0.123$
4,000-4,999	4	$\frac{4}{57}=0.070$
5,000-5,999	1	$\frac{1}{57}=0.018$
6,000-6,999	0	$\frac{0}{57}=0.000$
7,000-7,999	0	$\frac{0}{57}=0.000$
8,000-8,999	1	$\frac{1}{57}=0.018$
Total	57

Relative Frequency Histogram:

Software procedure:

• Step by step procedure to draw the relative frequency histogram for the number of words spoken using MINITAB software.
• Choose Graph > Histogram.
• Choose Simple.
• Click OK.
• In Graph variables, enter the column of Number of Words.
• In Scale, Choose Y-scale Type as Percent.
• Click OK.
• Select Edit Scale, Enter 0, 1,000, 2,000, 3,000, 4,000, 5,000, 6,000, 7,000, 8,000 and 9,000 in Positions of ticks.
• In Binning, Under Interval Type select Cutpoint and under Interval Definition select Number of intervals as 9 and Cutpoint positions as 0, 1,000, 2,000, 3,000, 4,000, 5,000, 6,000, 7,000, 8,000 and 9,000.
• In Labels, Enter 0, 1,000, 2,000, 3,000, 4,000, 5,000, 6,000, 7,000, 8,000 and 9,000in Specified.
• Click OK.

Observation:

From the bar graph, it can be seen that maximum number of words spoken is in the interval 1,000-2,000.

h.

To determine

Check whether the 9 and 5 classes are reasonable or one choice is much better than the other and explain the reason.

Answer to Problem 31E

Both the 5 and 9 classes are reasonable.

Explanation of Solution

Answer will vary.

The number of classes can be obtained by the following two points:

• The number of classes should be between 5 and 20.
• A larger number of classes will be appropriate for a very large data set.

Here number of classes for the histograms are 5 and 9 respectively. Thus, the number of classes are lies between 5 and 20.

Hence, the both 5 and 9 classes are reasonable.