
The point P(0.5, 0) lies on the curve y = cos πx.
(a) If Q is the point (x, cos πx), use your calculator to find the slope of the secant line PQ (.correct to six decimal places) for the following values of x:
(i) 0
(ii) 0.4
(iii) 0.49
(iv) 0.499
(v) 1
(vi) 0.6
(vii) 0.51
(viii) 0.501
(b) Using the result of part (a), guess the value of the slope of the tangent line to the curve at P(0.5, 0).
(c) Using the slope from part (b), find an equation of the tangent line to the curve at P(0.5, 0).
(d) Sketch the curve, two of the secant lines, and the tangent line.
(a)
To find: The slope of the secant line PQ for the following values of x.
Answer to Problem 4E
The slope of the secant line PQ for the following values of x is given below:
(i) The slope of the secant line PQ when
(ii) The slope of the secant line PQ when
(iii) The slope of the secant line PQ when
(iv) The slope of the secant line PQ when
(v) The slope of the secant line PQ when
(vi) The slope of the secant line PQ when
(vii) The slope of the secant line PQ when
(viii) The slope of the secant line PQ when
Explanation of Solution
Given:
The equation of the curve
The point P(0.5, 0) lies on the curve y.
The point Q is
Calculation:
The slope of the secant line between the points, P(0.5, 0) and Q
Section (i):
Obtain the slope of the secant line PQ when
Substitute 0 for x in
Substitute Q
Thus, the slope of the secant line PQ when
Section-(ii):
Obtain the slope of the secant line PQ when
Substitute 0.4 for x in
Substitute Q
Thus, the slope of the secant line PQ when
Section-(iii):
Obtain the slope of the secant line PQ when
Substitute 0.49 for x in
Substitute Q
Thus, the slope of the secant line PQ when
Section-(iv):
Obtain the slope of the secant line PQ when
Substitute 0.499 for x in
Substitute Q
Thus, the slope of the secant line PQ when
Section-(v):
Obtain the slope of the secant line PQ when
Substitute 1 for x in
Substitute Q
Thus, the slope of the secant line PQ when
Section-(vi):
Obtain the slope of the secant line PQ when
Substitute 0.6 for x in
Substitute Q
Thus, the slope of the secant line PQ when
Section-(vii):
Obtain the slope of the secant line PQ when
Substitute 0.49 for x in
Substitute Q
Thus, the slope of the secant line PQ when
Section-(viii):
Obtain the slope of the secant line PQ when
Substitute 0.501 for x in
Substitute Q
Thus, the slope of the secant line PQ when
(b)
To guess: The slope of the tangent line to the curve at P (0.5, 0).
Answer to Problem 4E
The estimated slope of the tangent line to the curve at P (0.5, 0) is
Explanation of Solution
Formula used:
The slope of the tangent line is the limit of the slope of the secant line.
That is,
Calculation:
From part (a), the slope of the secant line for many values of x is closer to 1. Thus, the slope
Substitute
Since
Thus, the estimated slope of the tangent line to the curve at P (0.5, 0) is
(c)
To find: The equation of the tangent line to the curve at P(0.5, 0).
Answer to Problem 4E
The equation of the tangent line to the curve at P(0.5, 0) is
Explanation of Solution
Formula used:
The equation of the tangent line to the curve
Calculation:
Substitute
Thus, the equation of the tangent line to the curve at P(0.5,0) is
(d)
To sketch: The curve, two of the secant line, and the tangent line.
Explanation of Solution
Formula used:
Slope-intercept formula:
Calculation:
Obtain the secant line at
The slope of the secant line PQ when
Use the slope-point intercept formula to find a equation of the secant line.
Substitute
Thus, the equation of the secant line at
Obtain the secant line at
The slope of the secant line PQ when
Use the slope-point intercept formula to find a equation of the secant line.
Substitute
Thus, the equation of the secant line at
Note that the equation of the secant line at
Draw the curve
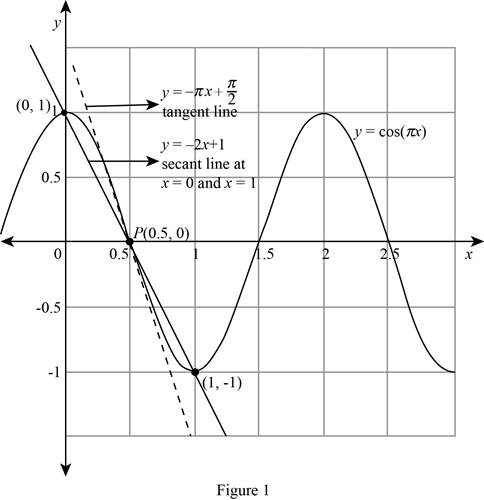
Thus, the required sketch is obtained.
Chapter 2 Solutions
Single Variable Calculus: Concepts and Contexts, Enhanced Edition
Additional Math Textbook Solutions
Pathways To Math Literacy (looseleaf)
A Problem Solving Approach To Mathematics For Elementary School Teachers (13th Edition)
Basic College Mathematics
Elementary Statistics Using The Ti-83/84 Plus Calculator, Books A La Carte Edition (5th Edition)
Elementary Statistics: A Step By Step Approach
Graphical Approach To College Algebra
- Suppose the number of people who register to attend the Tucson Festival of Books can be modeled by P(t) = k(1.1), where t is the number of days since the registration window opened. Assume k is a positive constant. Which of the following represents how long it will take in days for the number of people who register to double? t = In(1.1) In(2) In(2) t = In(1.1) In(1.1) t = t = t = In(2) - In(k) In(2) In(k) + In(1.1) In(2) - In(k) In(1.1)arrow_forwardUse the method of washers to find the volume of the solid that is obtained when the region between the graphs f(x) = √√2 and g(x) = secx over the interval ≤x≤ is rotated about the x-axis.arrow_forward5 Use the method of disks to find the volume of the solid that is obtained when the region under the curve y = over the interval [4,17] is rotated about the x-axis.arrow_forward
- 3. Use the method of washers to find the volume of the solid that is obtained when the region between the graphs f(x) = √√2 and g(x) = secx over the interval ≤x≤ is rotated about the x-axis.arrow_forward4. Use cylindrical shells to find the volume of the solid generated when the region enclosed by the given curves is revolved about the x-axis. y = √√x, y = 0, y = √√3arrow_forward5 4 3 21 N -5-4-3-2 -1 -2 -3 -4 1 2 3 4 5 -5+ Write an equation for the function graphed above y =arrow_forward
- 6 5 4 3 2 1 -5 -4-3-2-1 1 5 6 -1 23 -2 -3 -4 -5 The graph above is a transformation of the function f(x) = |x| Write an equation for the function graphed above g(x) =arrow_forwardThe graph of y x² is shown on the grid. Graph y = = (x+3)² – 1. +10+ 69 8 7 5 4 9 432 6. 7 8 9 10 1 10 -9 -8 -7 -6 -5 -4 -3 -2 -1 1 2 3 4 5 -2 -3 -4 -5 -6- Clear All Draw:arrow_forwardSketch a graph of f(x) = 2(x − 2)² − 3 4 3 2 1 5 ས་ -5 -4 -3 -2 -1 1 2 3 4 -1 -2 -3 -4 -5+ Clear All Draw:arrow_forward
- 5. Find the arc length of the curve y = 3x³/2 from x = 0 to x = 4.arrow_forward-6 -5 * 10 8 6 4 2 -2 -1 -2 1 2 3 4 5 6 -6 -8 -10- The function graphed above is: Concave up on the interval(s) Concave down on the interval(s) There is an inflection point at:arrow_forward6 5 4 3 2 1 -6 -5 -3 -2 3 -1 -2 -3 -4 -5 The graph above is a transformation of the function x² Write an equation for the function graphed above g(x) =arrow_forward
 Calculus: Early TranscendentalsCalculusISBN:9781285741550Author:James StewartPublisher:Cengage Learning
Calculus: Early TranscendentalsCalculusISBN:9781285741550Author:James StewartPublisher:Cengage Learning Thomas' Calculus (14th Edition)CalculusISBN:9780134438986Author:Joel R. Hass, Christopher E. Heil, Maurice D. WeirPublisher:PEARSON
Thomas' Calculus (14th Edition)CalculusISBN:9780134438986Author:Joel R. Hass, Christopher E. Heil, Maurice D. WeirPublisher:PEARSON Calculus: Early Transcendentals (3rd Edition)CalculusISBN:9780134763644Author:William L. Briggs, Lyle Cochran, Bernard Gillett, Eric SchulzPublisher:PEARSON
Calculus: Early Transcendentals (3rd Edition)CalculusISBN:9780134763644Author:William L. Briggs, Lyle Cochran, Bernard Gillett, Eric SchulzPublisher:PEARSON Calculus: Early TranscendentalsCalculusISBN:9781319050740Author:Jon Rogawski, Colin Adams, Robert FranzosaPublisher:W. H. Freeman
Calculus: Early TranscendentalsCalculusISBN:9781319050740Author:Jon Rogawski, Colin Adams, Robert FranzosaPublisher:W. H. Freeman
 Calculus: Early Transcendental FunctionsCalculusISBN:9781337552516Author:Ron Larson, Bruce H. EdwardsPublisher:Cengage Learning
Calculus: Early Transcendental FunctionsCalculusISBN:9781337552516Author:Ron Larson, Bruce H. EdwardsPublisher:Cengage Learning





