Chapter 2, Problem 19RE

To determine

To sketch: The graph of a function $f\left(x\right)=\frac{{\cos }^{2}x}{x^2}$ and discover the asymptotes.

Answer to Problem 19RE

The vertical asymptote of the function $f\left(x\right)=\frac{{\cos }^{2}x}{x^2}$ is $x=0$.

Explanation of Solution

Graph:

Use an online graphing calculator to draw the graph of $f$ as shown below in Figure 1.

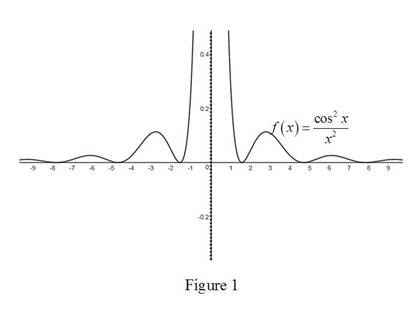
Observation:

From the above graph, it is observed that $x=0$ is the vertical asymptote to the function $f\left(x\right)=\frac{{\cos }^{2}x}{x^2}$.

Recall from the definition that $x=a$ is vertical asymptote if $\underset{x\to b}{\lim }f\left(x\right)=\infty$ or $\underset{x\to -b}{\lim }f\left(x\right)=\infty$.

Consider the function, $f\left(x\right)=\frac{{\cos }^{2}x}{x^2}$.

Take limit on the above expression

$\begin{array}{c}\underset{x\to 0}{\lim }f\left(x\right)=\underset{x\to 0}{\lim }\frac{{\cos }^{2}x}{x^2}\\ =\underset{x\to 0}{\lim }\left({\cos }^{2}x\right)\times \underset{x\to 0}{\lim }\left(\frac{1}{x^2}\right)\\ =\left({\cos }^{2}0\right)\times \left(\frac{1}{0^2}\right)\\ =\infty \end{array}$

Thus, $\underset{x\to 0}{\lim }f\left(x\right)=\infty$.

Thus, the vertical asymptote to the function $f\left(x\right)=\frac{{\cos }^{2}x}{x^2}$ is $x=0$.