Chapter 2.6, Problem 11E

(a)

To determine

To state: The position at which the particle is moving to the right, moving to the left and standing still on the time intervals.

Answer to Problem 11E

The particle is moving to the right on the time intervals (0, 1) and (4, 6).

The particle is moving to the left on the time interval (2, 3).

The particle is standing still on the time interval (1, 2) and (3, 4).

Explanation of Solution

Formula used:

The average velocity over the time interval $\left[a,a+h\right]$ is,

$\text{Average velocity}=\frac{\text{displacement}}{\text{time}}$

$=\frac{f\left(a+h\right)-f\left(a\right)}{\left(a+h\right)-a}$ (1)

Note 1: The average velocity is same as the instantaneous velocity when the particle is moving along a straight line.

Note 2: The particle is moving to the right when the velocity is positive.

Note 3: The particle is moving to the left when the velocity is negative.

Note 4: The particle is standing still when the velocity is zero.

Calculation:

At the time interval (0, 1):

From the given graph, it is observed that the straight line is passing through the points (0, 0) and (1,3).

Substitute (0, 0) for $\left(a,f\left(a\right)\right)$ and (1,3) for $\left(a+h,f\left(a+h\right)\right)$ in equation (1),

$\begin{array}{c}\text{Average velocity}=\frac{3-0}{1-0}\\ =\frac{3}{1}\\ =3\end{array}$

Thus, the average velocity of the particle moving along a straight line is $3\text{ m/s}$.

By Note 1, the velocity of the particle on the time interval (0, 1) is $3\text{ m/s}$.

By Note 2, the particle is moving to the right on the time interval (0, 1) since the velocity is positive.

Thus, the particle is moving to the right when $s\left(t\right)$ is increasing on the interval (0, 1).

At the time interval (1, 2):

From the given graph, it is observed that the straight line is passing through the points (1, 3) and (2,3).

Substitute (1, 3) for $\left(a,f\left(a\right)\right)$ and (2,3) for $\left(a+h,f\left(a+h\right)\right)$ in equation (1),

$\begin{array}{c}\text{Average velocity}=\frac{3-3}{2-1}\\ =\frac{0}{1}\\ =0\end{array}$

Thus, the average velocity of the particle moving along a straight line is $0\text{ m/s}$.

By Note 1, the velocity of the particle on the time interval (1, 2) is $0\text{ m/s}$.

By Note 4, the particle is standing still on the time interval (1, 2), since the velocity is zero.

Thus, the particle is standing still when $s\left(t\right)$ is constant on the interval (1, 2).

At the time interval (2, 3):

From the given graph, it is observed that the straight line is passing through the points (2, 3) and (3,1).

Substitute (2, 3) for $\left(a,f\left(a\right)\right)$ and (3,1) for $\left(a+h,f\left(a+h\right)\right)$ in equation (1),

$\begin{array}{c}\text{Average velocity}=\frac{1-3}{3-2}\\ =\frac{-2}{1}\\ =-2\end{array}$

Thus, the average velocity of the particle moving along a straight line is $-2\text{ m/s}$.

By Note 1, the velocity of the particle on the time interval (2, 3) is $-2\text{ m/s}$.

By Note 3, the particle is moving to the left on the time interval (2, 3), since the velocity is negative.

Thus, the particle is moving to the left when $s\left(t\right)$ is decreasing on the interval (2, 3).

At the time interval (3, 4):

From the given graph, it is observed that the straight line is passing through the points (3, 1) and (4, 1).

Substitute (3, 1) for $\left(a,f\left(a\right)\right)$ and (4, 1) for $\left(a+h,f\left(a+h\right)\right)$ in equation (1),

$\begin{array}{c}\text{Average velocity}=\frac{1-1}{4-3}\\ =\frac{0}{1}\\ =0\end{array}$

Thus, the average velocity of the particle moving along a straight line is $0\text{ m/s}$.

By Note 1, the velocity of the particle on the time interval (3, 4) is $0\text{ m/s}$.

By Note 4, the particle is standing still on the time interval (3, 4), since the velocity is zero.

Thus, the particle is standing still when $s\left(t\right)$ is constant on the interval (3, 4).

At the time interval (4, 6):

From the given graph, it is observed that the straight line is passing through the points (4, 1) and (6, 3).

Substitute (4, 1) for $\left(a,f\left(a\right)\right)$ and (6,3) for $\left(a+h,f\left(a+h\right)\right)$ in equation (1),

$\begin{array}{c}\text{Average velocity}=\frac{3-1}{6-4}\\ =\frac{2}{2}\\ =1\end{array}$

Thus, the average velocity of the particle moving along a straight line is $\text{1 m/s}$.

By Note 1, the velocity of the particle on the time interval (4, 6) is $3\text{ m/s}$.

By Note 2, the particle is moving to the right on the time interval (4, 6), since the velocity is positive.

Thus, the particle is moving to the right when $s\left(t\right)$ is increasing on the interval (4, 6).

(b)

To determine

To sketch: The graph of the velocity function.

Explanation of Solution

Time-velocity table:

Use part (a) to make the time-velocity table as shown below.

Time interval (in seconds)	(0, 1)	(1, 2)	(2,3)	(3, 4)	(4, 6)
Velocity (in m/s)	3	0	−2	0	1

Use the above table to draw the velocity function for the corresponding time intervals as shown in Figure 1.

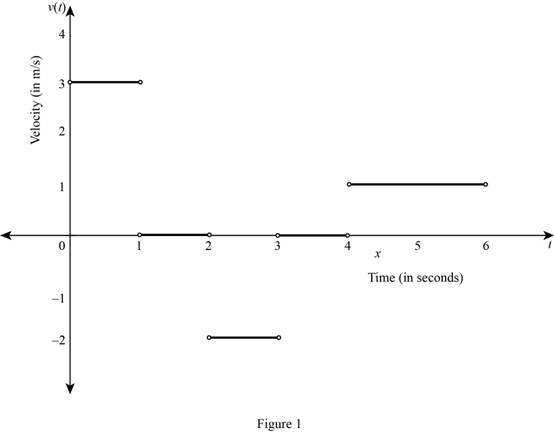
From Figure 1, it is observed that there is no slope at the end points and the velocity is constant at each time interval.