
Concept explainers
In Example 21.4, suppose the point charge on the y-axis at y = −0.30 m has negative charge −2.0μC, and the other charges remain the same. Find the magnitude and direction of the net force on Q. How does your answer differ from that in Example 21.4? Explain the differences.
Example 21.4 VECTOR ADDITION OF ELECTRIC FORCES
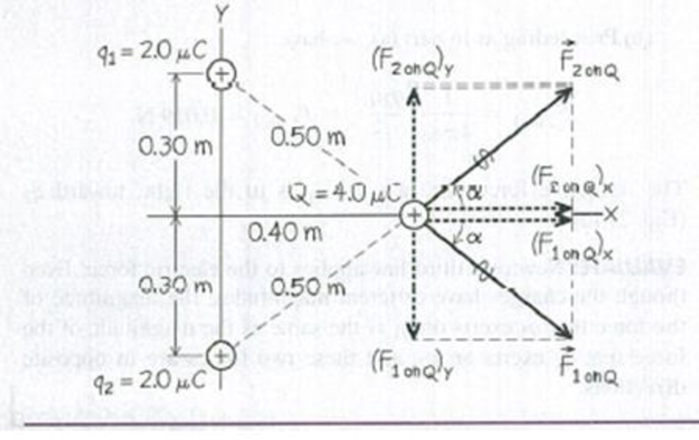
Two equal positive charges q1 – q2 – 2.0 μC are located at x = 0, y = 0.30 m and x = 0, y = −0.30 m. respectively. What are the magnitude and direction of the total electric force that q1 and q2 exert on a third charge Q = 4.0 μC at x = 0.40 m, y = 0?
SOLUTION
IDENTIFY and SET UP: As in Example 21.3, we must compute the force that each charge exerts on Q and then find the vector sum of those forces. Figure 21.14 shows the situation. Since the three charges do not all lie on a line, the best way to calculate the forces is to use components.
Figure 21.14 Our sketch for this problem.
Learn your wayIncludes step-by-step video

Chapter 21 Solutions
University Physics with Modern Physics Plus Mastering Physics with eText -- Access Card Package (14th Edition)
Additional Science Textbook Solutions
Modern Physics
Glencoe Physical Science 2012 Student Edition (Glencoe Science) (McGraw-Hill Education)
Physics for Scientists and Engineers: A Strategic Approach, Vol. 1 (Chs 1-21) (4th Edition)
The Cosmic Perspective (8th Edition)
Life in the Universe (4th Edition)
Conceptual Integrated Science
- Particle A of charge 3.00 104 C is at the origin, particle B of charge 6.00 104 C is at (4.00 m, 0), and particle C of charge 1.00 104 C is at (0, 3.00 m). We wish to find the net electric force on C. (a) What is the x component of the electric force exerted by A on C? (b) What is the y component of the force exerted by A on C? (c) Find the magnitude of the force exerted by B on C. (d) Calculate the x component of the force exerted by B on C. (e) Calculate the y component of the force exerted by B on C. (f) Sum the two x components from parts (a) and (d) to obtain the resultant x component of the electric force acting on C. (g) Similarly, find the y component of the resultant force vector acting on C. (h) Find the magnitude and direction of the resultant electric force acting on C.arrow_forward(a) Two point charges q1 and q23.00 m apart, and their total charge is 20 C. (a) If the force of repulsion between them is 0.075N, what are magnitudes of the two charges? (b) If one charge attracts the other with a force of 0.150 N, what are the magnitudes of the two charges? Note that you may need to solve a quadratic equation to reach your answer.arrow_forwardTwo point charges attract each other with an electric force of magnitude F. If the charge on one of the particles is reduced to one-third its original value and the distance between the particles is doubled, what is the resulting magnitude of the electric force between them? (a) 112F (b) 13F (c) 16F (d) 34F (e) 32Farrow_forward
- Eight charged panicles, each of magnitude q, are located on the corners of a cube of edge s as shown in Figure P22.48. (a) Determine the x, y, and z components of the total force exerted by the other charges on the charge located at point A. What are (b) the magnitude and (c) the direction of this total force? Figure P22.48arrow_forward(a) What is the electric field 5.00 m from the center of the terminal of a Van de Graaff with a 3.00 mC charge, noting that the field is equivalent to that of a point charge at the center of the terminal? (b) At this distance, what force does the field exert on a 2.00 C charge on the Van de Graaff’s belt?arrow_forwardAssume the charged objects in Figure OQ23.10 are fixed. Notice that there is no sight line from the location of q2 to the location of q1. If you were at q1, you would be unable to see q2 because it is behind q3. How would you calculate the electric force exerted on the object with charge q1? (a) Find only the force exerted by q2 on charge q1. (b) Find only the force exerted by q3 an charge q1. (c) Add the force that q2 would exert by itself on charge q1 to the force that q3 would exert by itself on charge q1. (d) Add the force that q3 would exert by itself to a certain fraction of the force that q2 would exert by itself. (e) There is no definite way to find the force on charge q1.arrow_forward
- Two point charges qA = 12.0 C and qB = 45.0 C and a third particle with unknown charge qC are located on the x axis. The particle qA is at the origin, and qB is at x = 15.0 cm. The third particle is to be placed so that each particle is in equilibrium under the action of the electric forces exerted by the other two particles. (a) Is this situation possible? If so, is it possible in more than one way? Explain. Find (b) the required location and (c) the magnitude and the sign of the charge of the third particle.arrow_forward(a) What is the electric field 5.00 m from die center of the terminal of a Van de Graaff with a 3.00-mC charge, noting that the field is equivalent to that of a point charge at the center of the terminal? (b) At this distance, what force does the field exert on a 2.00C charge on the Van de Graaff’s belt?arrow_forwardPanicle A of charge 3.00 104 C is at the origin, particle B of charge 6.00 104 C is at (4.00 m, 0), and panicle C of charge 1.00 104 C is at (0, 3.00 m). (a) What is the x-component of the electric force exerted by A on C? (b) What is the y-component of the force exerted by A on C? (c) Find the magnitude of the force exerted by B on C. (d) Calculate the x-component of the force exerted by B on C. (e) Calculate the y-component of the force exerted by B on C. (f) Sum the two x-components to obtain the resultant x-component of the electric force acting on C. (g) Repeat part (f) for the y-component. (h) Find the magnitude and direction of the resultant electric force acting on C.arrow_forward
- A test charge of +3 C is at a point P where an external electric field is directed to the right and has a magnitude of 4 06 N/C. If the test charge is replaced with another charge of 3 C, what happens to the external electric field at P? (a) It is unaffected. (b) It reverses direction. (c) It changes in a way that cannot be determined.arrow_forwardAssume the charged objects in Figure OQ19.15 are fixed. Notice that there is no sight line from the location of q2 to the location of q1. If you were at q1, you would be unable to see q2 because it is behind q3. How would you calculate the electric force exerted on the object with charge q1? (a) Find only the force exerted by q2 on charge q1. (b) Find only the force exerted by q3 on charge q1. (c) Add the force that q2 would exert by itself on charge q1 to the force that q3 would exert by itself on charge q1. (d) Add the force that q3 would exert by itself to a certain fraction of the force that q2 would exert by itself. (e) There is no definite way to find the force on charge q1. Figure OQ19.15arrow_forwardThree point charges are arranged as shown in Figure P19.19. (a) Find the vector electric Field that the 6.00-nC and 3.00-nC charges together create at the origin. (b) Find the vector force on the 5.00-nC charge.arrow_forward
 Principles of Physics: A Calculus-Based TextPhysicsISBN:9781133104261Author:Raymond A. Serway, John W. JewettPublisher:Cengage Learning
Principles of Physics: A Calculus-Based TextPhysicsISBN:9781133104261Author:Raymond A. Serway, John W. JewettPublisher:Cengage Learning Physics for Scientists and Engineers, Technology ...PhysicsISBN:9781305116399Author:Raymond A. Serway, John W. JewettPublisher:Cengage Learning
Physics for Scientists and Engineers, Technology ...PhysicsISBN:9781305116399Author:Raymond A. Serway, John W. JewettPublisher:Cengage Learning Physics for Scientists and Engineers: Foundations...PhysicsISBN:9781133939146Author:Katz, Debora M.Publisher:Cengage Learning
Physics for Scientists and Engineers: Foundations...PhysicsISBN:9781133939146Author:Katz, Debora M.Publisher:Cengage Learning Physics for Scientists and EngineersPhysicsISBN:9781337553278Author:Raymond A. Serway, John W. JewettPublisher:Cengage Learning
Physics for Scientists and EngineersPhysicsISBN:9781337553278Author:Raymond A. Serway, John W. JewettPublisher:Cengage Learning Physics for Scientists and Engineers with Modern ...PhysicsISBN:9781337553292Author:Raymond A. Serway, John W. JewettPublisher:Cengage Learning
Physics for Scientists and Engineers with Modern ...PhysicsISBN:9781337553292Author:Raymond A. Serway, John W. JewettPublisher:Cengage Learning College PhysicsPhysicsISBN:9781938168000Author:Paul Peter Urone, Roger HinrichsPublisher:OpenStax College
College PhysicsPhysicsISBN:9781938168000Author:Paul Peter Urone, Roger HinrichsPublisher:OpenStax College





