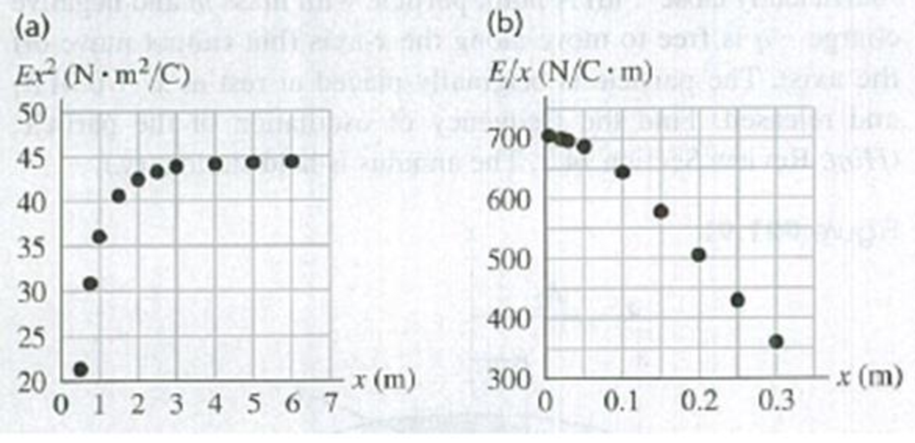
Problem 21.1DQ: If you peel two strips of transparent tape off the same roll and immediately let them hang near each... Problem 21.2DQ: Two metal spheres are hanging from nylon threads. When you bring the spheres close to each other,... Problem 21.3DQ: The electric force between two charged particles becomes weaker with increasing distance. Suppose... Problem 21.4DQ: Your clothing tends to cling together after going through the dryer. Why? Would you expect more or... Problem 21.5DQ: An uncharged metal sphere hangs from a nylon thread. When a positively charged glass rod is brought... Problem 21.6DQ: BIO Estimate how many electrons there are in your body. Make any assumptions you feel are necessary,... Problem 21.7DQ: Figure Q2I.7 shows some of the electric field lines due to three point charges arranged along the... Problem 21.8DQ: Good conductors of electricity, such as metals, are typically good conductors of heat; insulators,... Problem 21.9DQ: Suppose that the charge shown in Fig. 21.28a is fixed in position. A small, positively charged... Problem 21.10DQ: Two identical metal objects are mounted on insulating stands. Describe how you could place charges... Problem 21.11DQ: Because the charges on the electron and proton have the same absolute value, atoms are electrically... Problem 21.12DQ: If you walk across a nylon rug and then touch a large metal object such as a doorknob, you may get a... Problem 21.13DQ: You have a negatively charged object. How can you use it to place a net negative charge on an... Problem 21.14DQ: When two point charges of equal mass and charge are released on a frictionless table, each has an... Problem 21.15DQ: A point charge of mass m and charge Q and another point charge of mass m but charge 2Q are released... Problem 21.16DQ: A proton is placed in a uniform electric field and then released. Then an electron is placed at this... Problem 21.17DQ: In Example 21.1 (Section 21.3) we saw that the electric force between two particles is of the order... Problem 21.18DQ: What similarities do electric forces have with gravitational forces? What are, the most significant... Problem 21.19DQ: Two irregular objects A and B carry charges of opposite sign. Figure Q21.19 shows the electric field... Problem 21.20DQ: Atomic nuclei are made of protons and neutrons. This shows that there must be another kind of... Problem 21.21DQ: Sufficiently strong electric fields can cause atoms to become positively ionizedthat is, to lose one... Problem 21.22DQ: The electric fields at point P due to the positive charges q1 and q2 are shown in Fig. Q21.22. Does... Problem 21.23DQ: The air temperature and the velocity of the air have different values at different places in the... Problem 21.1E: Excess electrons are placed on a small lead sphere with mass 8.00 g so that its net charge is 3.20 ... Problem 21.2E: Lightning occurs when there is a flow of electric charge (principally electrons) between the ground... Problem 21.3E: If a proton and an electron are released when they are 2.0 1010 m apart (a typical atomic... Problem 21.4E: Particles in a Gold Ring. You have a pure (24-karat) gold ring of mass 10.8 g. Gold has an atomic... Problem 21.5E: BIO Signal Propagation in Neurons. Neurons are components of the nervous system of the body that... Problem 21.6E: Two small spheres spaced 20.0 cm apart have equal charge. How many excess electrons must be present... Problem 21.7E: An average human weighs about 650 N. If each of two average humans could carry 1.0 C of excess... Problem 21.8E: Two small aluminum spheres, each having mass 0.0250 kg, are separated by 80.0 cm. (a) How many... Problem 21.9E: Two small plastic spheres are given positive electric charges. When they are 15.0 cm apart, the... Problem 21.10E: Just How Strong Is the Electric Force? Suppose you had two small boxes, each containing 1.0 g of... Problem 21.11E: In an experiment in space, one proton is held fixed and another proton is released from rest a... Problem 21.12E: A negative charge of 0.550 C exerts an upward 0.600-N force on an unknown charge that is located... Problem 21.13E: Three point charges are arranged on a line. Charge q3 = +5.00 nC and is at the origin. Charge q2 =... Problem 21.14E: In Example 21.4, suppose the point charge on the y-axis at y = 0.30 m has negative charge 2.0C, and... Problem 21.15E: In Example 21.3, calculate the net force on charge q1. Problem 21.16E: In Example 21.4, what is the net force (magnitude and direction) on charge q1 exerted by the other... Problem 21.17E: Three point charges are arranged along the .x-axis. Charge q1 = +3.00 C is at the origin, and charge... Problem 21.18E: Repeat Exercise 21.17 for q3 = +8.00 C. Problem 21.19E: Two point charges are located on the y-axis as follows: charge q1 = 1.50 nC at y = 0.600 m, and... Problem 21.20E: Two point charges are placed on the .x -axis as follows: Charge q1 = +4.00 nC is located at x =... Problem 21.21E: BIO Base Pairing in DNA, I. The two sides of the DNA double helix are connected by pairs of bases... Problem 21.22E: BIO Base Pairing in DNA, II. Refer to Exercise 21.21. Figure E21.22 shows the bonding of cytosine... Problem 21.23E: CP A proton is placed in a uniform electric field of 2.75 103 N/C. Calculate (a) the magnitude of... Problem 21.24E: A particle has charge 5.00 nC. (a) Find the magnitude and direction of the electric field due to... Problem 21.25E: CP A proton is traveling horizontally to the right at 4.50 106 m/s. (a) Find the magnitude and... Problem 21.26E: CP An electron is released from rest in a uniform electric field. The electron accelerates... Problem 21.27E: (a) What must the charge (sign and magnitude) of a 1.45-g particle be for it to remain stationary... Problem 21.28E: Electric Field of the Earth. The earth has a net electric charge that causes a field at points near... Problem 21.29E: CP An electron is projected with an initial speed 0 = 1.60 106 m/s into the uniform field between... Problem 21.30E: (a) Calculate the magnitude and direction (relative to the +.x-axis) of the electric field in... Problem 21.31E: CP In Exercise 21.29, what is the speed of the electron as it emerges from the field? Problem 21.32E: CP A uniform electric field exists in the region between two oppositely charged plane parallel... Problem 21.33E: A point charge is at the origin. With this point charge as the source point, what is the unit vector... Problem 21.34E: A +8.75-C point charge is glued down on a horizontal frictionless table. It is tied to a 6.50-C... Problem 21.35E: (a) An electron is moving east in a uniform electric field of 1.50 N/C directed to the west. At... Problem 21.36E: Two point charges Q and +q (where q is positive) produce the net electric field shown at point P in... Problem 21.37E: Two positive point charges q are placed on the .x-axis, one at x = a and one at .x = a. (a) Find the... Problem 21.38E: The two charges q1 and q2 shown in Fig. E21.38 have equal magnitudes. What is the direction of the... Problem 21.39E: A +2.00-nC point charge is at the origin, and a second 5.00-nC point charge is on the x-axis at x =... Problem 21.40E: Repeat Exercise 21.39, hut now let the charge at the origin be 4.00 nC. Problem 21.41E: Three negative point charges lie along a line as shown in Fig. E21.41. Find the magnitude and... Problem 21.42E: A point charge is placed at each corner of a square with side length a. All charges have magnitude... Problem 21.43E: Two point charges are separated by 25.0 cm (Fig. E21.43). Find the net electric field these charges... Problem 21.44E: Point charge q1 = 5.00 nC is at the origin and point charge q2 = +3.00 nC is on the x-axis at x =... Problem 21.45E: If two electrons are each 1.50 1010 m from a proton (Fig. E21.45), find the magnitude and direction... Problem 21.46E: BIO Electric Field of Axons. A nerve signal is transmitted through a neuron when an excess of Na+... Problem 21.47E: In a rectangular coordinate system a positive point charge q = 6.00 109 C is placed at the point x... Problem 21.48E: A point charge q1 = 4.00 nC is at the point x = 0.600 m, y = 0.800 m, and a second point charge q2 =... Problem 21.49E: A charge of 6.50nC is spread uniformly over the surface of one face of a nonconducting disk of... Problem 21.50E: A very long, straight wire has charge per unit length 3.20 1010 C/m. At what distance from the wire... Problem 21.51E: A ring-shaped conductor with radius a = 2.50 cm has a total positive charge Q = +0.125 nC uniformly... Problem 21.52E: A straight, nonconducting plastic wire 8.50 cm long carries a charge density of +175nC/m distributed... Problem 21.53E: Point charges q1 = 4.5 nC and q2 = +4.5 nC are separated by 3.1 mm, forming an electric dipole. (a)... Problem 21.54E: The ammonia molecule (NH3) has a dipole moment of 5.0 1030Cm. Ammonia molecules in the gas phase... Problem 21.55E: Torque on a Dipole. An electric dipole with dipole moment p is in a uniform external electric field... Problem 21.56E: The dipole moment of the water molecule (H2O) is 6.17 1030Cm. Consider a water molecule located at... Problem 21.57E: Three charges are at the corners of an isosceles triangle as shown in Fig. E21.57. The 5.00-C... Problem 21.58E: Consider the electric dipole of Example 21.14. (a) Derive an expression for the magnitude of the... Problem 21.59P: Four identical charges Q are placed at the corners of a square of side L. (a) In a free-body... Problem 21.60P: Two charges are placed on the x-axis: one, of 2.50 C, at the origin and the other, of 3.50 C, at x =... Problem 21.61P: A charge q1 = +5.00 nC is placed at the origin of an xy-coordinate system, and a charge q2 = 2.00 nC... Problem 21.62P: CP Two identical spheres with mass m are hung from silk threads of length L (Fig. P21.62). The... Problem 21.63P: CP Two small spheres with mass m = 15.0 g are hung by silk threads of length L = 1.20 m from a... Problem 21.64P: CP Two identical spheres are each attached to silk threads of length L = 0.500 m and hung from a... Problem 21.65P: CP A small 12.3-g plastic ball is tied to a very light 28.6-cm string that is attached to the... Problem 21.66P: Point charge q1 = 6.00 106 C is on the x-axis at x = 0.200 m. Point charge q2 is on the x-axis at x... Problem 21.67P: Two particles having charges q1 = 0.500 nC and q2 = 8.00 nC are separated by a distance of 1.20 m.... Problem 21.68P: A 3.00-nC point charge is on the x-axis at x = 1.20 m. A second point charge, Q, is on the x-axis at... Problem 21.69P: A charge +Q is located at the origin, and a charge + 4Q is at distance d away on the x-axis. Where... Problem 21.70P: A charge of 3.00 nC is placed at the origin of an xy-coordinate system, and a charge of 2.00 nC is... Problem 21.71P: Three identical point charges q are placed at each of three corners of a square of side L. Find the... Problem 21.72P: Two point charges q1 and q2 are held in place 4.50 cm apart. Another point charge Q = 1.75 C, of... Problem 21.73P: CP Strength of the Electric Force. Imagine two 1.0-g bags of protons, one at the earths north pole... Problem 21.74P: CP Two tiny spheres of mass 6.80 mg carry charges of equal magnitude, 72.0 nC, but opposite sign.... Problem 21.75P: CP Consider a model of a hydrogen atom in which an electron is in a circular orbit of radius r =... Problem 21.76P: The earth has a downward-directed electric field near its surface of about 150 N/C. If a raindrop... Problem 21.77P: CP A proton is projected into a uniform electric field that points vertically upward and has... Problem 21.78P: A small object with mass m, charge q, and initial speed v0 = 5.00 103 m/s is projected into a... Problem 21.79P: CALC Positive charge Q is distributed uniformly along the x-axis from x = 0 to x = a. A positive... Problem 21.80P: In a region where there is a uniform electric field that is upward and has magnitude 3.60 104 N/C,... Problem 21.81P: A negative point charge q1 = 4.00 nC is on the x-axis at x = 0.60 m. A second point charge q2 is on... Problem 21.82P: CALC Positive charge Q is distributed uniformly along the positive y-axis between y = 0 and y = a. A... Problem 21.83P: A uniformly charged disk like the disk in Fig. 21.25 has radius 2.50 cm and carries a total charge... Problem 21.84P: CP A small sphere with mass m carries a positive charge q and is attached to one end of silk fiber... Problem 21.85P: CALC Negative charge Q is distributed uniformly around a quarter-circle of radius a that lies in the... Problem 21.86P: CALC A semicircle of radius a is in the first and second quadrants, with the center of curvature at... Problem 21.87P: Two 1.20-m non- conducting rods meet at a right angle. One rod carries +2.50 C of charge distributed... Problem 21.88P: Two very large parallel sheets are 5.00 cm apart. Sheet A carries a uniform surface charge density... Problem 21.89P: Repeat Problem 21.88 for the case where sheet B is positive. 21.88 Two very large parallel sheets... Problem 21.90P: Two very large horizontal sheets are 4.25 cm apart and carry equal but opposite uniform surface... Problem 21.91P: CP A thin disk with a circular hole at its center, called an annulus, has inner radius R1 and outer... Problem 21.92P: DATA CP Design of an Inkjet Printer. Inkjet printers can be described as either continuous or... Problem 21.93P: DATA Two small spheres, each carrying a net positive charge, are separated by 0.400 m. You have been... Problem 21.94P: DATA Positive charge Q is distributed uniformly around a very thin conducting ring of radius a, as... Problem 21.95CP: Three charges are placed as shown in Fig. P21.95. The magnitude of q1 is 2.00 C, but its sign and... Problem 21.96CP: Two charges are placed as shown in Fig. P21.96. The magnitude of q1 is 3.00 C, but its sign and the... Problem 21.97CP: CALC Two thin rods of length L lie along the x-axis, one between x=12a and x=12a+L and the other... Problem 21.98PP: BIO ELECTRIC BEES. Flying insects such as bees may accumulate a small positive electric charge as... Problem 21.99PP: BIO ELECTRIC BEES. Flying insects such as bees may accumulate a small positive electric charge as... Problem 21.100PP: After one bcc left a flower with a positive charge, that bee flew away and another bcc with the same... Problem 21.101PP: In a follow-up experiment, a charge of +40 pC was placed at the center of an artificial flower at... format_list_bulleted


 College PhysicsPhysicsISBN:9781938168000Author:Paul Peter Urone, Roger HinrichsPublisher:OpenStax College
College PhysicsPhysicsISBN:9781938168000Author:Paul Peter Urone, Roger HinrichsPublisher:OpenStax College Physics for Scientists and Engineers: Foundations...PhysicsISBN:9781133939146Author:Katz, Debora M.Publisher:Cengage Learning
Physics for Scientists and Engineers: Foundations...PhysicsISBN:9781133939146Author:Katz, Debora M.Publisher:Cengage Learning College PhysicsPhysicsISBN:9781305952300Author:Raymond A. Serway, Chris VuillePublisher:Cengage Learning
College PhysicsPhysicsISBN:9781305952300Author:Raymond A. Serway, Chris VuillePublisher:Cengage Learning Physics for Scientists and Engineers, Technology ...PhysicsISBN:9781305116399Author:Raymond A. Serway, John W. JewettPublisher:Cengage Learning
Physics for Scientists and Engineers, Technology ...PhysicsISBN:9781305116399Author:Raymond A. Serway, John W. JewettPublisher:Cengage Learning Principles of Physics: A Calculus-Based TextPhysicsISBN:9781133104261Author:Raymond A. Serway, John W. JewettPublisher:Cengage Learning
Principles of Physics: A Calculus-Based TextPhysicsISBN:9781133104261Author:Raymond A. Serway, John W. JewettPublisher:Cengage Learning





