Concept explainers
Videos
(a)
To identify: Whether there is any instant at which the two bicycles have the same velocity.
(a)
Answer to Problem 85GP
Yes, there is one point where the two bicycles have the same velocity. It is when the slopes of both the functions are parallel.
Explanation of Solution
Given:
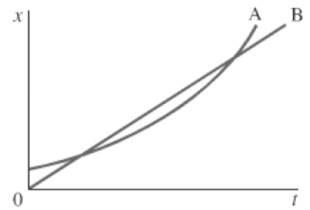
The given position-time for two bicycles is shown below.
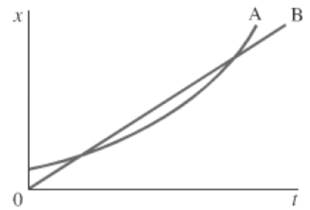
Formula used:
The slope of a function in a position time graph provides the velocity of the moving object.
Calculation:
Consider the given graph. Slopes of parallel lines are equal. B is a straight line, so it will have a constant slope. A is a curve, hence its slope varies while moving from bottom to top. At the point of maximum curvature, A’s slope is the same as B. At this instant, both A and B have the same velocity.
Conclusion:
Therefore, for the given graph there is a point when velocity of both the bicycles is same.
(b)
The bicycle that will have larger acceleration.
(b)
Answer to Problem 85GP
Bicycle A has a larger acceleration.
Explanation of Solution
Given:
The given position-time for two bicycles is shown below.
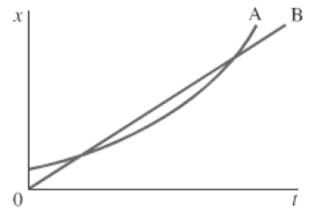
Formula used:
The slope of a function in a position time graph is the velocity of the moving object.
Calculation:
Bicycle B depicts a straight line in the position time graph. Hence its slope is constant. Since the slope is constant, the acceleration is 0. Bicycle A is represented by a curve, which means that its slope, and hence its velocity changes. From the graph, it is evident that the slope keeps increasing.
Conclusion:
Therefore, bicycle A has a larger acceleration
(c)
The instants at which the bicycles passing each other. Also, the bicycle that will pass the another bicycle.
(c)
Answer to Problem 85GP
At the points of intersections in the graph, the bicycles pass each other. First bicycle B will pass bicycle A and then bicycle A will pass bicycle B.
Explanation of Solution
Given:
The given position-time for two bicycles is shown below.
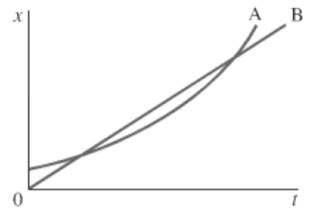
Calculation:
The graph plots position against time. Thus, it shows the position of an object at different instances of time. If the functions for A and B intersect, then, it means that both A and B are at the same position at that particular instant. Therefore, the bicycles have to pass each other at points of intersections.
From the given graph, it is observed that at the first intersection point bicycle B will pass bicycle but later on at the second point of intersection, bicycle A will pass bicycle B.
Conclusion:
Therefore, both bicycles will meet at point of intersection and will pass each other.
(d)
The bicycle that will have the highest instantaneous velocity.
(d)
Answer to Problem 85GP
Before the instant of time where their velocities are equal, bicycle B has the higher instantaneous velocity after which Bicycle A has the higher velocity.
Explanation of Solution
Given:
The given position-time for two bicycles is shown below.
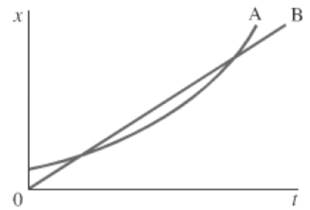
Formula used:
The slope at particular point of position time graph defines the instantaneous velocity of a moving object.
Calculation:
The slope at a point in the position-time graph gives the velocity of the bicycle at that instant. bicycle B has constant slope since it is a straight line. The slope of the curve representing bicycle A shows an increase from bottom to top. Thus, till the instant where the slopes are equal, bicycle B has a higher instantaneous velocity. After this point, bicycle A, whose slope keeps increasing will have a higher instantaneous velocity.
Conclusion:
Therefore, bicycle B will have greatest instantaneous velocity and then later on A will have greatest velocity.
(e)
The bicycle that will have higher average velocity.
(e)
Answer to Problem 85GP
Both the bicycles must havethe same average velocity.
Explanation of Solution
Given:
The given position-time for two bicycles is shown below.
Formula used:
The slope of a function in a position time graph is the velocity of the moving object. The average velocity is the ratio of total displacement and total time taken
Calculation:
Bicycle B is depicted by a straight line. Its velocity is constant. For A, the displacement is lesser but the total time taken is also lesser. So, the average velocity for both the bicycles A and B should have almost the same value.
Conclusion:
Therefore, both bicycles will have same average velocity.
Chapter 2 Solutions
Physics: Principles with Applications
Additional Science Textbook Solutions
Campbell Biology in Focus (2nd Edition)
Physics for Scientists and Engineers: A Strategic Approach, Vol. 1 (Chs 1-21) (4th Edition)
Introductory Chemistry (6th Edition)
College Physics: A Strategic Approach (3rd Edition)
Applications and Investigations in Earth Science (9th Edition)
Organic Chemistry (8th Edition)
- suggest a reason ultrasound cleaning is better than cleaning by hand?arrow_forwardCheckpoint 4 The figure shows four orientations of an electric di- pole in an external electric field. Rank the orienta- tions according to (a) the magnitude of the torque on the dipole and (b) the potential energy of the di- pole, greatest first. (1) (2) E (4)arrow_forwardWhat is integrated science. What is fractional distillation What is simple distillationarrow_forward
- 19:39 · C Chegg 1 69% ✓ The compound beam is fixed at Ę and supported by rollers at A and B. There are pins at C and D. Take F=1700 lb. (Figure 1) Figure 800 lb ||-5- F 600 lb بتا D E C BO 10 ft 5 ft 4 ft-—— 6 ft — 5 ft- Solved Part A The compound beam is fixed at E and... Hình ảnh có thể có bản quyền. Tìm hiểu thêm Problem A-12 % Chia sẻ kip 800 lb Truy cập ) D Lưu of C 600 lb |-sa+ 10ft 5ft 4ft6ft D E 5 ft- Trying Cheaa Những kết quả này có hữu ích không? There are pins at C and D To F-1200 Egue!) Chegg Solved The compound b... Có Không ☑ ||| Chegg 10 וחarrow_forwardNo chatgpt pls will upvotearrow_forwardNo chatgpt pls will upvotearrow_forward
- No chatgpt pls will upvotearrow_forwardair is pushed steadily though a forced air pipe at a steady speed of 4.0 m/s. the pipe measures 56 cm by 22 cm. how fast will air move though a narrower portion of the pipe that is also rectangular and measures 32 cm by 22 cmarrow_forwardNo chatgpt pls will upvotearrow_forward
- 13.87 ... Interplanetary Navigation. The most efficient way to send a spacecraft from the earth to another planet is by using a Hohmann transfer orbit (Fig. P13.87). If the orbits of the departure and destination planets are circular, the Hohmann transfer orbit is an elliptical orbit whose perihelion and aphelion are tangent to the orbits of the two planets. The rockets are fired briefly at the depar- ture planet to put the spacecraft into the transfer orbit; the spacecraft then coasts until it reaches the destination planet. The rockets are then fired again to put the spacecraft into the same orbit about the sun as the destination planet. (a) For a flight from earth to Mars, in what direction must the rockets be fired at the earth and at Mars: in the direction of motion, or opposite the direction of motion? What about for a flight from Mars to the earth? (b) How long does a one- way trip from the the earth to Mars take, between the firings of the rockets? (c) To reach Mars from the…arrow_forwardNo chatgpt pls will upvotearrow_forwarda cubic foot of argon at 20 degrees celsius is isentropically compressed from 1 atm to 425 KPa. What is the new temperature and density?arrow_forward
College PhysicsPhysicsISBN:9781305952300Author:Raymond A. Serway, Chris VuillePublisher:Cengage Learning
University Physics (14th Edition)PhysicsISBN:9780133969290Author:Hugh D. Young, Roger A. FreedmanPublisher:PEARSON
Introduction To Quantum MechanicsPhysicsISBN:9781107189638Author:Griffiths, David J., Schroeter, Darrell F.Publisher:Cambridge University Press
Physics for Scientists and EngineersPhysicsISBN:9781337553278Author:Raymond A. Serway, John W. JewettPublisher:Cengage Learning
Lecture- Tutorials for Introductory AstronomyPhysicsISBN:9780321820464Author:Edward E. Prather, Tim P. Slater, Jeff P. Adams, Gina BrissendenPublisher:Addison-Wesley
College Physics: A Strategic Approach (4th Editio...PhysicsISBN:9780134609034Author:Randall D. Knight (Professor Emeritus), Brian Jones, Stuart FieldPublisher:PEARSON