Essential University Physics: Volume 1; Mastering Physics with Pearson eText -- ValuePack Access Card -- for Essential University Physics (3rd Edition)
3rd Edition
ISBN: 9780134197319
Author: Richard Wolfson
Publisher: PEARSON
expand_more
expand_more
format_list_bulleted
Videos
Textbook Question
Chapter 19, Problem 42P
A 0.20-mol sample of an ideal gas goes through the Carnot cycle of Fig. 19.23. Calculate (a) the heat Qh absorbed, (b) the heat Qc rejected, and (c) the work done, (d) Use these quantities to determine the efficiency, (c) Find the maximum and minimum temperatures, and show explicitly that the efficiency as defined in Equation 19.1 is equal to the Carnot efficiency of Equation 19.3.
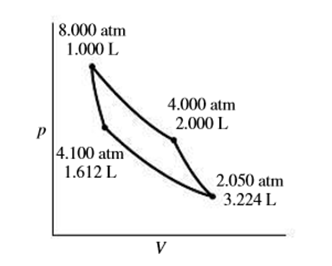
FIGURE 19.23 Problem 42
Expert Solution & Answer
Want to see the full answer?
Check out a sample textbook solution
Students have asked these similar questions
A 2.00-mol sample of a diatomic ideal gas expands slowly and adiabatically from a pressure of 5.02 atm and a volume of 12.2 L to a final volume of 29.2 L.
(a) What is the final pressure of the gas?
atm
(b) What are the initial and final temperatures?
initial
K
final
K
(c) Find Q for the gas during this process.
kJ
(d) Find AE
for the gas during this process.
int
kJ
(e) Find W for the gas during this process.
k)
Five moles of Nitrogen (behaving like an ideal gas) are taken around cycle acb as shown. Process ac is at constant pressure, process ba is at constant volume, and process cb is adiabatic. The temperatures at each part of the process are Ta = 300 K, Tb = 600 K, and Tc = 492 K.
a) What is the change in internal energy of the gas during process ac?(b) How much work is done during ac?(c) Assume that at point a, Pa = 3 ×104 Pa and Va = 0.5 m3. What is the volume at point c?(d) What is the pressure at point b?(e) How much work is done during the whole cycle? Is it done by the gas or on the gas (by the surround-ings)?
Suppose 1.0 mol of a monatomic ideal gas initially at 10 L and 300 K is heated at constant volume to 600 K, allowed to expand isothermally to its initial pressure, and finally compressed at constant pressure to its original volume, pressure, and temperature. During the cycle, what are (a) the net energy entering the system (the gas) as heat and (b) the net work done by the gas? (c) What is the efficiency of the cycle?
Chapter 19 Solutions
Essential University Physics: Volume 1; Mastering Physics with Pearson eText -- ValuePack Access Card -- for Essential University Physics (3rd Edition)
Ch. 19.1 - Which of these processes is irreversible? (a)...Ch. 19.2 - The low temperature for a practical heat engine is...Ch. 19.3 - A clever engineer decides to increase the...Ch. 19.4 - In each of the following processes, does the...Ch. 19 - Could you cool the kitchen by leaving the...Ch. 19 - Prob. 2FTDCh. 19 - Should a car get better mileage in the summer or...Ch. 19 - Prob. 4FTDCh. 19 - Name some irreversible processes that occur in a...Ch. 19 - Your power company claims that electric heat is...
Ch. 19 - A hydroelectric power plant, using the energy of...Ch. 19 - A heat-pump manufacturer claims the device will...Ch. 19 - Prob. 9FTDCh. 19 - The heat Q added during adiabatic free expansion...Ch. 19 - Energy is conserved, so why cant we recycle it as...Ch. 19 - Why doesnt the evolution of human civilization...Ch. 19 - What are the efficiencies of reversible heat...Ch. 19 - A cosmic heat engine might operate between the...Ch. 19 - A reversible Carnot engine operating between...Ch. 19 - A Carnot engine absorbs 900 J of heat each cycle...Ch. 19 - Find the COP of a reversible refrigerator...Ch. 19 - Prob. 18ECh. 19 - The human body can be 25% efficient at converting...Ch. 19 - Calculate the entropy change associated with...Ch. 19 - You metabolize a 650-kcal burger at your 37C body...Ch. 19 - You heat 250 g of water from 10C to 95C. By how...Ch. 19 - Melting a block of lead already at its melting...Ch. 19 - How much energy becomes unavailable for work in an...Ch. 19 - Prob. 25ECh. 19 - A Carnot engine extracts 745 J from a 592-K...Ch. 19 - The maximum steam temperature in a nuclear power...Ch. 19 - Youre engineering an energy-efficient house that...Ch. 19 - A power plants electrical output is 750 MW....Ch. 19 - A power plant extracts energy from steam at 280C...Ch. 19 - The electric power output of all the thermal...Ch. 19 - Consider a Carnot engine operating between...Ch. 19 - An industrial freezer operates between 0C and 32C,...Ch. 19 - Use appropriate energy-flow diagrams to analyze...Ch. 19 - Prob. 35PCh. 19 - A refrigerator maintains an interior temperature...Ch. 19 - You operate a store thats heated by an oil furnace...Ch. 19 - Use energy-flow diagrams to show that the...Ch. 19 - A heat pump extracts energy from groundwater at...Ch. 19 - A reversible engine contains 0.350 mol of ideal...Ch. 19 - (a) Determine the efficiency for the cycle shown...Ch. 19 - A 0.20-mol sample of an ideal gas goes through the...Ch. 19 - A shallow pond contains 94 Mg of water. In winter,...Ch. 19 - Estimate the rate of entropy increase associated...Ch. 19 - The temperature of n moles of ideal gas is changed...Ch. 19 - The temperature of n moles of ideal gas is changed...Ch. 19 - A 6.36-mol sample of ideal diatomic gas is at 1.00...Ch. 19 - A 250-g sample of water at 80C is mixed with 250 g...Ch. 19 - An ideal gas undergoes a process that takes it...Ch. 19 - In an adiabatic free expansion, 6.36 mol of ideal...Ch. 19 - Find the entropy change when a 2.4-kg aluminum pan...Ch. 19 - An engine with mechanical power output 8.5 kW...Ch. 19 - Find the change in entropy as 2.00 kg of H2O at...Ch. 19 - Gasoline engines operate approximately on the Otto...Ch. 19 - The compression ratio r of an engine is the ratio...Ch. 19 - In a diesel cycle, gas at volume V1 and pressure...Ch. 19 - (a) Show that the heal flowing into the diesel...Ch. 19 - Youre considering buying a car that comes in...Ch. 19 - The 54-M W wood-fired McNeil Generating Station in...Ch. 19 - A 500-g copper block at 80C is dropped into 1.0 kg...Ch. 19 - An objects heat capacity is inversely proportional...Ch. 19 - A Carnot engine extracts heat from a block of mass...Ch. 19 - In an alternative universe, youve got the...Ch. 19 - Youre the environmental protection officer for a...Ch. 19 - Find an expression for the entropy gain when hot...Ch. 19 - Problem 74 of Chapter 16 provided an approximate...Ch. 19 - The molar specific heat at constant pressure for a...Ch. 19 - Prob. 68PCh. 19 - Energy-efficiency specialists measure the heat Qh...Ch. 19 - Refrigerators remain among the greatest consumers...Ch. 19 - The refrigerators COP is a. 13. b. 2. c. 3. d. 4.Ch. 19 - The fuel energy consumed at the power plant to run...Ch. 19 - Prob. 73PP
Additional Science Textbook Solutions
Find more solutions based on key concepts
Acetobacter is necessary for only one of the steps of vitamin C manufacture. The easiest way to accomplish this...
Microbiology: An Introduction
APPLY 1.2 Express the following quantities in scientific notation
using fundamental SI units of mass and lengt...
Chemistry (7th Edition)
What are four functions of connective tissue?
Anatomy & Physiology (6th Edition)
Which of the following factors would tend to increase membrane fluidity? A. a greater proportion of unsaturated...
Campbell Biology in Focus (2nd Edition)
1.3 Obtain a bottle of multivitamins and read the list of ingredients. What are four chemicals from the list?
Chemistry: An Introduction to General, Organic, and Biological Chemistry (13th Edition)
Based on your answers to Questions 2 and 3, which part of the Atlantic basin appears to have opened first?
Applications and Investigations in Earth Science (9th Edition)
Knowledge Booster
Learn more about
Need a deep-dive on the concept behind this application? Look no further. Learn more about this topic, physics and related others by exploring similar questions and additional content below.Similar questions
- A copper rod of cross-sectional area 5.0 cm2 and length 5.0 m conducts heat from a heat reservoir at 373 K to one at 273 K. What is the time rate of change of the universe's entropy for this process?arrow_forwardTwo moles of a monatomic ideal gas such as oxygen is compressed adiabatically and reversibly from a state (3 atm, 5 L) to a state with a pressure of 4 atm. (a) Find the volume and temperature of the final state. (b) Find the temperature of the initial state. (c) Find work done by the gas in the process. (d) Find the change in internal energy in the process. Assume Cv=5R and Cp=Cv+R for the diatomic ideal gas in the conditions given.arrow_forwardAt point A in a Carnot cycle, 2.34 mol of a monatomic ideal gas has a pressure of 1 4000 kPa, a volume of 10.0 L, and a temperature of 720 K. The gas expands isothermally to point B and then expands adiabatically to point C, where its volume is 24.0 L. An isothermal compression brings it to point D, where its volume is 15.0 L. An adiabatic process returns the gas to point A. (a) Determine all the unknown pressures, volumes, and temperatures as you f ill in the following table: (b) Find the energy added by heat, the work done by the engine, and the change in internal energy for each of the steps A B, B C, C D, and D A (c) Calculate the efficiency Wnet/|Qk|. (d) Show that the efficiency is equal to 1 - TC/TA, the Carnot efficiency.arrow_forward
- An ideal gas with specific heat ratio confined to a cylinder is put through a closed cycle. Initially, the gas is at Pi, Vi, and Ti. First, its pressure is tripled under constant volume. It then expands adiabatically to its original pressure and finally is compressed isobarically to its original volume. (a) Draw a PV diagram of this cycle. (b) Determine the volume at the end of the adiabatic expansion. Find (c) the temperature of the gas at the start of the adiabatic expansion and (d) the temperature at the end of the cycle. (e) What was the net work done on the gas for this cycle?arrow_forwardA car tile contains 0.0380 m3 of air at a pressure of 2.20105 Pa (about 32 psi). How much more internal energy does this gas have than the same volume has at zero gauge pressure (which is equivalent to normal atmospheric pressure)?arrow_forwardA 1.00-mol sample of an ideal monatomic gas is taken through the cycle shown in Figure P18.63. The process AB is a reversible isothermal expansion. Calculate (a) the net work done by the gas, (b) the energy added to the gas by heat, (c) the energy exhausted from the gas by heat, and (d) the efficiency of the cycle. (e) Explain how the efficiency compares with that of a Carnot engine operating between the same temperature extremes. Figure P18.63arrow_forward
- As shown below, calculate the work done by the gas in the quasi-static processes represented by the paths (a) AB; (b) ADB; (c) ACB; and (d) ADCB. `arrow_forwardA cylinder containing three moles of a monatomic ideal gas is heated at a constant pressure of 2 atm. The temperature of the gas changes from 300 K to 350 K as a result of the expansion. Find work done (a) on the gas; and (b) by the gas.arrow_forwardAn amount of n moles of a monatomic ideal gas in a conducting container with a movable piston is placed in a large thermal heat bath at temperature T1 and the gas is allowed to come to equilibrium. After the equilibrium is leached, the pressure on the piston is lowered so that the gas expands at constant temperature. The process is continued quasi-statically until the final pressure is 4/3 of the initial pressure p1 . (a) Find the change in the internal energy of the gas. (b) Find the work done by the gas. (c) Find the heat exchanged by the gas, and indicate, whether the gas takes in or gives up heat.arrow_forward
- A multicylinder gasoline engine in an airplane, operating at 2.50 103 rev/min, takes in energy 7.89 103 J and exhausts 4.58 103 J for each revolution of the crankshaft. (a) How many liters of fuel does it consume in 1.00 h of operation if the heat of combustion of the fuel is equal to 4.03 107 J/L? (b) What is the mechanical power output of the engine? Ignore friction and express the answer in horsepower. (c) What is the torque exerted by the crankshaft on the load? (d) What power must the exhaust and cooling system transfer out of the engine?arrow_forwardTwo moles of an ideal gas with the heat capacity per mole Cp=7R/2 at constant pressure go through the cycle acb shown below. You are given the temperatures at those three points as Ta, Tb and Tc, respectively. Process cb is adiabatic. (i) What is the heat transferred to the gas during ac process? (ii) Calculate the total work for the whole cycle using the given parameters only. (R: gas constant) P b a Varrow_forwardAs shown in the figure, a container with a moveable piston and containing a monatomic ideal gas in an initial state A undergoes an isovolumetric, then an isothermal, and finally an isobaric process to complete the cycle. P (atm) C V (L) 0 When the gas is in the initial state, the volume is 7.00 L, the pressure is 3.00 atm, and the temperature is 350 K. The gas is first warmed at constant volume to a pressure of 4 times the initial value (state B). The gas is then allowed to expand isothermally to some new volume (state C). Finally it is compressed isobarically to its initial state. (Due to the nature of this problem, do not use rounded intermediate values in your calculations-including answers submitted in WebAssign.) (a) Find the number of moles of the gas. moles (b) Find the temperature of the gas at state B (in K). K (c) Find the temperature of the gas at state C (in K). K B Aarrow_forward
arrow_back_ios
SEE MORE QUESTIONS
arrow_forward_ios
Recommended textbooks for you
Principles of Physics: A Calculus-Based TextPhysicsISBN:9781133104261Author:Raymond A. Serway, John W. JewettPublisher:Cengage Learning
Physics for Scientists and Engineers, Technology ...PhysicsISBN:9781305116399Author:Raymond A. Serway, John W. JewettPublisher:Cengage Learning
Physics for Scientists and Engineers: Foundations...PhysicsISBN:9781133939146Author:Katz, Debora M.Publisher:Cengage Learning
Principles of Physics: A Calculus-Based Text
Physics
ISBN:9781133104261
Author:Raymond A. Serway, John W. Jewett
Publisher:Cengage Learning
Physics for Scientists and Engineers, Technology ...
Physics
ISBN:9781305116399
Author:Raymond A. Serway, John W. Jewett
Publisher:Cengage Learning
Physics for Scientists and Engineers: Foundations...
Physics
ISBN:9781133939146
Author:Katz, Debora M.
Publisher:Cengage Learning
The Second Law of Thermodynamics: Heat Flow, Entropy, and Microstates; Author: Professor Dave Explains;https://www.youtube.com/watch?v=MrwW4w2nAMc;License: Standard YouTube License, CC-BY