Chapter 18, Problem 63P

A 1.00-mol sample of an ideal monatomic gas is taken through the cycle shown in Figure P18.63. The process A→B is a reversible isothermal expansion. Calculate (a) the net work done by the gas, (b) the energy added to the gas by heat, (c) the energy exhausted from the gas by heat, and (d) the efficiency of the cycle. (e) Explain how the efficiency compares with that of a Carnot engine operating between the same temperature extremes.

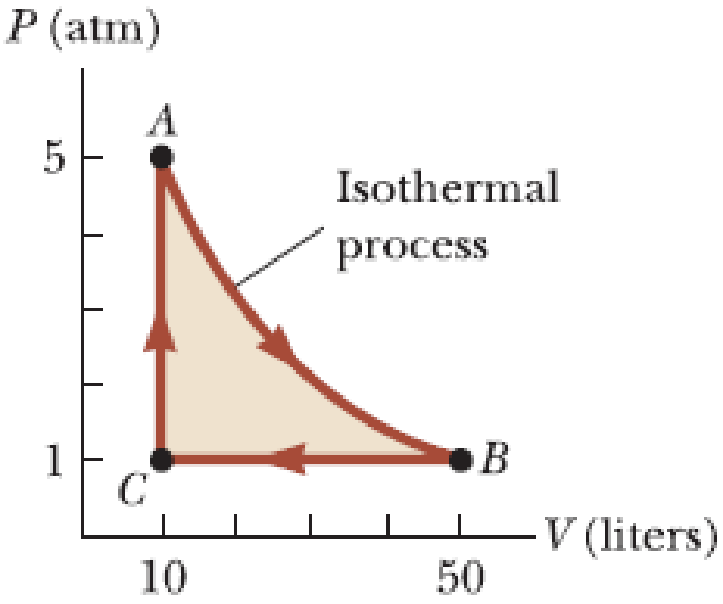
Figure P18.63

To determine

Net work done by the gas.

Answer to Problem 63P

Net work done by the gas is $\underset{\_}{4.10\text{kJ}}$.

Explanation of Solution

For an isothermal process AB, the work on the gas is

    $W_{AB}=-P_A{V}_A\ln \left(\frac{V_B}{V_A}\right)$        (I)

Here $P_A$ is the pressure at A, $V_A$ is the volume at A and $V_B$ is the volume at B.

Write the equation for work done in the process BC,

    $W_{BC}=-P_B\left(V_A-V_B\right)$        (II)

Here $P_B$ is the pressure at B.

Work done in the process CA is zero because the volume is constant.

Write the equation for met work done

    $W_{\text{eng}}=-W_{AB}-W_{BC}$        (III)

Conclusion:

Substitute $5\text{atm}$ for $P_A$, $50\text{L}$ for $V_B$ and $10\text{L}$ for $V_A$ in (I)

    $\begin{array}{c}{W}_{AB}=-5\text{atm}\left(\frac{1.013\times {10}^5\text{Pa}}{1\text{atm}}\right)\left(10\text{L}\left(\frac{{10}^{-3}{\text{m}}^{\text{3}}}{1\text{L}}\right)\right)\ln \left(\frac{50\text{L}}{10\text{L}}\right)\\ =-\left(5\times 1.013\times {10}^5\text{Pa}\right)\left(10\times {10}^{-3}{\text{m}}^{\text{3}}\right)\ln \left(\frac{50\text{L}}{10\text{L}}\right)\\ =-8.15\times {10}^3\text{J}\end{array}$

Substitute $1\text{atm}$ for $P_B$, $50\text{L}$ for $V_B$ and $10\text{L}$ for $V_A$ in (II)

    $\begin{array}{c}{W}_{BC}=-\left(1\text{atm}\left(\frac{1.013\times {10}^5\text{Pa}}{1\text{atm}}\right)\right)\left(10\text{L}\left(\frac{{10}^{-3}{\text{m}}^{\text{3}}}{1\text{L}}\right)-50\text{L}\left(\frac{{10}^{-3}{\text{m}}^{\text{3}}}{1\text{L}}\right)\right)\\ =\left(1\times 1.013\times {10}^5\text{Pa}\right)\left(10\times {10}^{-3}{\text{m}}^{\text{3}}-50\times {10}^{-3}{\text{m}}^{\text{3}}\right)\\ =4.05\times {10}^3\text{J}\end{array}$

Substitute $-8.15\times {10}^3\text{J}$ for $W_{AB}$ and $4.05\times {10}^3\text{J}$ for $W_{BC}$ in (III)

    $\begin{array}{c}{W}_{\text{eng}}=-\left(-8.15\times {10}^3\text{J}\right)-4.05\times {10}^3\text{J}\\ =4.10\text{kJ}\end{array}$

Net work done by the gas is $\underset{\_}{4.10\text{kJ}}$.

To determine

Energy added to the gas by heat.

Answer to Problem 63P

Total energy absorbed by heat is $\underset{\_}{1.42\times {10}^4\text{J}}$.

Explanation of Solution

The change in internal energy for the process AB is zero as it is isothermal.

Then,

    $Q_{AB}=-W_{AB}$        (IV)

Write the equation for specific heat capacity at constant volume

    $C_V=\frac{3R}{2}$        (V)

Here $R$ is the real gas constant.

Write the ideal gas equation in terms of temperature

    $\begin{array}{c}{T}_B=T_A\\ =\frac{P_B{V}_B}{nR}\end{array}$        (VI)

Similarly,

    $T_C=\frac{P_C{V}_C}{nR}$        (VII)

Here $n$ is the number of moles, $P_C$ is the pressure at C and $V_C$ is the volume at C.

Write the equation for heat transfer for the process CA,

    $Q_{CA}=n\frac{3R}{2}\left(T_A-T_C\right)$        (VIII)

Substitute (V) in (VIII)

    $Q_{CA}=n{C}_V\left(T_B-T_C\right)$        (IX)

Write the equation for total energy absorbed by heat

    $Q_h=Q_{AB}+Q_{CA}$        (X)

Conclusion:

Substitute $1\text{atm}$ for $P_B$, $50\text{L}$ for $V_B$ and $1$ for $n$ in (VI)

    $\begin{array}{c}{T}_A=\frac{\left(1\text{atm}\left(\frac{1.013\times {10}^5\text{Pa}}{1\text{atm}}\right)\right)\left(50\text{L}\left(\frac{{10}^{-3}{\text{m}}^{\text{3}}}{1\text{L}}\right)\right)}{R}\\ =\frac{\left(1\times 1.013\times {10}^5\text{Pa}\right)\left(50\times {10}^{-3}{\text{m}}^{\text{3}}\right)}{R}\\ =\frac{5.06\times {10}^3}{R}\end{array}$

Substitute $1\text{atm}$ for $P_C$, $1$ for $n$ and $10\text{L}$ for $V_C$ in(VII)

    $\begin{array}{c}{T}_C=\frac{\left(1\text{atm}\left(\frac{1.013\times {10}^5\text{Pa}}{1\text{atm}}\right)\right)\left(10\text{L}\left(\frac{{10}^{-3}{\text{m}}^{\text{3}}}{1\text{L}}\right)\right)}{R}\\ =\frac{\left(1\times 1.013\times {10}^5\text{Pa}\right)\left(10\times {10}^{-3}{\text{m}}^{\text{3}}\right)}{R}\\ =\frac{1.01\times {10}^3}{R}\end{array}$

Substitute $1$ for $n$, $\frac{1.01\times {10}^3}{R}$ for $T_C$ and $\frac{5.06\times {10}^3}{R}$ for $T_A$ in (IX)

    $\begin{array}{c}{Q}_{CA}=\left(1\right)\frac{3}{2}R\left(\frac{5.06\times {10}^3}{R}-\frac{1.01\times {10}^3}{R}\right)\\ =6.08\text{kJ}\end{array}$

Substitute $8.15\text{kJ}$ for $Q_{AB}$ and $6.08\text{kJ}$ for $Q_{CA}$ in (X)

    $\begin{array}{c}{Q}_h=8.15\text{kJ}+6.08\text{kJ}\\ =1.42\times {10}^4\text{J}\end{array}$

Total energy absorbed by heat is $\underset{\_}{1.42\times {10}^4\text{J}}$

To determine

Energy exhausted from the gas by heat.

Answer to Problem 63P

The energy exhausted is $\underset{\_}{1.01\times {10}^4\text{J}}$.

Explanation of Solution

Write the equation for heat energy transferred

    $Q_{BC}=n{C}_P\Delta T$        (XI)

Here $C_P$ is the specific heat at constant pressure

Substitute $\frac{5R}{2}$ for $C_P$ in (IX)

    $\begin{array}{c}{Q}_{BC}=n\frac{5R}{2}\Delta T\\ =\frac{5}{2}\left(nR\Delta T\right)\end{array}$        (XII)

Substitute $nR\Delta T=P_B\Delta V_{BC}$ by ideal gas equation in (XII)

    $Q_{BC}=\frac{5}{2}\left(P_B\left(V_C-V_B\right)\right)$        (XIII)

Conclusion:

Substitute $1\text{atm}$ for $P_B$, $50\text{L}$ for $V_B$ and $10\text{L}$ for $V_C$ in (XIII)

    $\begin{array}{c}{Q}_{BC}=\frac{5}{2}\left(\left(1\text{atm}\left(\frac{1.013\times {10}^5\text{Pa}}{1\text{atm}}\right)\right)\left(10\text{L}\left(\frac{{10}^{-3}{\text{m}}^{\text{3}}}{1\text{L}}\right)-50\text{L}\left(\frac{{10}^{-3}{\text{m}}^{\text{3}}}{1\text{L}}\right)\right)\right)\\ =1.01\times {10}^4\text{J}\end{array}$

The energy exhausted is $\underset{\_}{1.01\times {10}^4\text{J}}$.

To determine

Efficiency of the cycle.

Answer to Problem 63P

The efficiency is $\underset{\_}{28.9\%}$.

Explanation of Solution

Write the equation for efficiency an engine in terms of work done

  $e=\frac{W_{\text{eng}}}{Q_h}$        (XIV)

Here $e$ is the efficiency, $W_{\text{eng}}$ is the work done by the engine and $Q_h$ is the heat in the hot reservoir.

Conclusion:

Substitute $4.1\times {10}^3\text{J}$ for $W_{\text{eng}}$ and $1.42\times {10}^4\text{J}$ for $Q_h$ in (XIV)

    $\begin{array}{c}e=\frac{4.1\times {10}^3\text{J}}{1.42\times {10}^4\text{J}}\\ =0.289\\ =28.9\%\end{array}$

The efficiency is $\underset{\_}{28.9\%}$.

To determine

Compare with the efficiency of a Carnot engine.

Answer to Problem 63P

The efficiency of this system is lower than the Carnot engine

Explanation of Solution

Write the equation for efficiency of a Carnot engine

    $e_c=1-\frac{T_c}{T_h}$        (XV)

Here $T_c$ is the temperature of the cold reservoir and $T_h$ is the temperature of the cold reservoir.

Conclusion:

Substitute $\frac{5060}{R}$ for $T_h$ and $\frac{1010}{R}$ for $T_h$ in (XV)

    $\begin{array}{c}{e}_c=1-\frac{\frac{1010}{R}}{\frac{5060}{R}}\\ =0.80\\ =80\%\end{array}$

The efficiency of this system is much lower than the Carnot engine