
Concept explainers
a)
1)
To determine: The system utilization rate.
Introduction: System utilization refers to percentage amount of capacity which is utilized or we can say that actual output is divided by potential output. It is operational metric for business which indicates aggregate productive capacity.
It reflects the ratio of demand to capacity or supply, it is also commonly known as Capacity utilization rate.
a)
1)
Answer to Problem 1P
Explanation of Solution
Given information:
Formula,
Where,
System utilization rate denoted by
Demand rate (measured as arrival) denoted by
Supply rate (measured as service) denoted by
Calculation of the system utilization:
Therefore, system utilization rate is 0.6000.
1)
To determine: The system utilization rate.
Introduction: System utilization refers to percentage amount of capacity which is utilized or we can say that actual output is divided by potential output. It is operational metric for business which indicates aggregate productive capacity.
It reflects the ratio of demand to capacity or supply, it is also commonly known as Capacity utilization rate.
1)
Answer to Problem 1P
Explanation of Solution
Given information:
Formula,
Where,
System utilization rate denoted by
Demand rate (measured as arrival) denoted by
Supply rate (measured as service) denoted by
Calculation of the system utilization:
Therefore, system utilization rate is 0.6000.
2)
To determine: The average number customers waiting for service in line.
2)
Answer to Problem 1P
Explanation of Solution
Explanation
Given information:
Formula as per single server model of average number customers waiting for service in line
Where,
Demand rate (measured as arrival) denoted by
Supply rate per server denoted by
Calculation of Average number of customers waiting in line (Lq):
Therefore, average number of customers waiting in line (Lq) is 0.9000.
3)
To determine: Average number of customers waiting time.
3)
Answer to Problem 1P
Explanation of Solution
Given information:
Formula as per single server model of average number customers waiting for service in line:
Where,
Demand rate (measured as arrival) denoted by
Calculation of Average number of customers waiting in line (
Therefore, average number customers waiting time (
b)
1)
To determine: The average number of customer waiting for repairs.
b)
1)
Answer to Problem 1P
Explanation of Solution
Given information:
Mean service time: 2 hours
M =1
Calculation of
Formula as per single server model of average number customers waiting for service in line:
Where,
Demand rate (measured as arrival) denoted by
Supply rate per server denoted by
Calculation of Average number of customers waiting in line (Lq):
Therefore, Average number of customers waiting in line (Lq) is 2.250.
1)
To determine: The average number of customer waiting for repairs.
1)
Answer to Problem 1P
Explanation of Solution
Given information:
Mean service time: 2 hours
M =1
Calculation of
Formula as per single server model of average number customers waiting for service in line:
Where,
Demand rate (measured as arrival) denoted by
Supply rate per server denoted by
Calculation of Average number of customers waiting in line (Lq):
Therefore, Average number of customers waiting in line (Lq) is 2.250.
2)
To determine: The system utilization rate.
Introduction: It reflects the ratio of demand to capacity or supply, it is also commonly known as Capacity utilization rate.
2)
Answer to Problem 1P
Explanation of Solution
Given information:
Formula,
Where,
System utilization rate denoted by
Demand rate (measured as arrival) denoted by
Supply rate (measured as service) denoted by
Calculation of the system utilization:
Therefore, system utilization rate is 0.750.
3)
To determine: The idle time.
3)
Answer to Problem 1P
Explanation of Solution
Calculation of the idle time:
Therefore, idle time per day per hours is 2hours per day.
4)
To determine: Probability of two or more customers in the system.
4)
Answer to Problem 1P
Explanation of Solution
Step 1: Calculate the probability of less than two:
Therefore, probability of less than two is 0.4375.
Step 2: Calculation probability of two or more than customer in the system:
Therefore, probability of less than two is 0.5625.
c)
1)
To determine: The system utilization rate.
c)
1)
Answer to Problem 1P
Explanation of Solution
Given information
Formula:
Where,
System utilization rate denoted by
Demand rate (measured as arrival) denoted by
Supply rate (measured as service) denoted by
Calculation of the system utilization:
Therefore, system utilization rate is 0.7500.
1)
To determine: The system utilization rate.
1)
Answer to Problem 1P
Explanation of Solution
Given information
Formula:
Where,
System utilization rate denoted by
Demand rate (measured as arrival) denoted by
Supply rate (measured as service) denoted by
Calculation of the system utilization:
Therefore, system utilization rate is 0.7500.
2)
To determine: Average number of customers in the system (Ls).
2)
Answer to Problem 1P
Explanation of Solution
Step 1: Calculation of the average number of customer served
Therefore average number of customer served is 1.5.
Step 2: find the value of
Given information:
Then, from Infinite-source values table we find that value for
For reference:
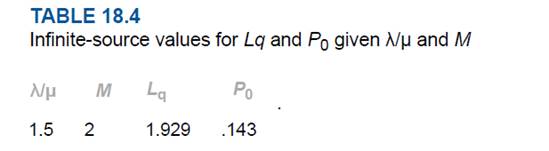
Step 3: Calculation of the average number of customers in the system (Ls)
Therefore, the average number of customers in the system (Ls) is 3.429.
3)
To determine: Average time customers wait in line for service (Wq).
3)
Answer to Problem 1P
Explanation of Solution
Therefore, the average time customers wait in line for service (Wq).is 0.107.
4)
To determine: The average waiting time for an arrival not immediately served (hours) (Wa).
4)
Answer to Problem 1P
Explanation of Solution
Calculation of average waiting time for an arrival not immediately served (hours) (Wa):
Therefore, average waiting time for an arrival not immediately served (hours) (Wa) is 0.167 hours.
Want to see more full solutions like this?
Chapter 18 Solutions
Operations Management
- Subway with more than 27,000 outlets in the US is planning for a new restaurant in Buffalo New York. A) Based on the given information, the best location in Buffalo for Subway to open the new restaurant is Baptist Church with a total weighted score of? (Enter your response rounded to two decimal places.) B) If the weights for Space and Traffic density are reversed, the best location in Buffalo for Subway to open the new restaurant will be with a total weighted score of ? (Enter your response rounded to two decimal places.)arrow_forwardnortheastern insurance company is considering opening an office in the US. The two cities under consideration are going to be Philadelphia New York. Factor ratings (higher scores are better) are in the table. The best location for northeastern insurance company to open would be which with a total weighted score of ? (response rounded to two decimal places)arrow_forwardWhen football fans watch a game, they believe the other side commits more infractions on the field than does their own team. This favoritism can best be termed _____. Group of answer choices A. ethnocentrism B. the fundamental attribution error C. the affiliation bias D. marginalizationarrow_forward
- When football fans watch a game, they believe the other side commits more infractions on the field than does their own team. This favoritism can best be termed _____. Group of answer choices ethnocentrism the fundamental attribution error the affiliation bias marginalizationarrow_forwardWhich of the following best describes the differences between egalitarianism and hierarchy as cultural values in negotiation? Group of answer choices A. Egalitarian cultures communicate directly; hierarchical cultures communicate indirectly. B. Egalitarian cultures treat people equally; hierarchical cultures discriminate among people. C. Egalitarian cultures divide things equally; hierarchical cultures divide things according to merit and status. D. Egalitarian cultures believe that status is permeable through effort and achievement; hierarchical cultures believe that superiors should take care of the needs of subordinates.arrow_forwardWhich of the following best describes the differences between individualism and collectivism as cultural values in negotiation? Group of answer choices A. Individualists see themselves as autonomous entities; collectivists see themselves in relation to others. B. Individualists prefer to work in groups; collectivists prefer to work alone. C. Individualists are cooperative; collectivists are competitive. D. Individualists focus on relationships; collectivists focus on money.arrow_forward
- When it comes to resolving conflict, managers from hierarchical cultures prefer _____. Group of answer choices A. to attribute a disagreeable person's behavior to an underlying disposition and desire formal dispute resolution procedures B. an interests model that relies on resolving underlying conflicts C. to regulate behavior via public shaming D. to defer to a higher status personarrow_forwardThe tripartite model of culture is based on three cultural prototypes that represent negotiators’ self-views and are highly correlated with particular geographic regions. Give an example of the three. Face Dignity Honorarrow_forwardThe personality and unique character of a social group is best known as its _____ and includes the values and norms shared by its members and encompasses the structure of its social, political, economic, and religious institutions. Group of answer choices group identity group potency group stereotype culturearrow_forward
- agree or disagree with this post Face - “Face” or dignity in a negotiation has been called “one of an individual’s most sacred possessions.”102 Face is the value a person places on his or her public image, reputation, and status vis-à-vis other people in the negotiation. Direct threats to face in a negotiation include making ultimatums, criticisms, challenges, and insults (Thompson, 2019). A good example of face is when I go to the negotiation table with a counterpart that is known to be difficult or not as knowledgeable about the category as they should be, my approach wouldn't be to point out their weakness, I will respect their thought process, show consideration for their perspective, all while guiding the conversation in the direction of my intended negotiation strategy in hopes to achieve my desired outcome. Dignity - endorses views such as, “People should stand up for what they believe in, even when others disagree,” and “How much a person respects oneself is far more…arrow_forward16:53 ◄ Mail 5G CSTUDY_Jan25_SCMH_O...Final_20250220143201.pdf CHOOSING FORECASTING MODELS gradienting are more mode. Yet when selecting a forecasting method, the door forecasts in fact, each of the three methods has different strength and can play important ing importance of the factors, such as the index and cast model, or a unified approach, ch del runs individual series separately A galable manufacturer is facing changes with demand fuctuations due to economiyapply make changes. Comment on why this has been the case and propose a forecasting approach that can be utilised t Question 13 ashit from a batch production process to a continuous flows to enhance efficiency. Critically analyse the trade- A public hospital in Free State is experiencing increasing patient wait times due to limited operacity. The hospital management is considering either expanding existing facilities orating more efficient Question 1.5 A farming consponsible for planting grain crops in Free State As expected…arrow_forwardHow can a college basketball coach use lean system strategies to improve the team's performance and win the national championship? What wastes can be eliminated from the team's training and equipment? How can performance data be used to adjust the team's strategy and tactics?arrow_forward
 Practical Management ScienceOperations ManagementISBN:9781337406659Author:WINSTON, Wayne L.Publisher:Cengage,MarketingMarketingISBN:9780357033791Author:Pride, William MPublisher:South Western Educational Publishing
Practical Management ScienceOperations ManagementISBN:9781337406659Author:WINSTON, Wayne L.Publisher:Cengage,MarketingMarketingISBN:9780357033791Author:Pride, William MPublisher:South Western Educational Publishing


