
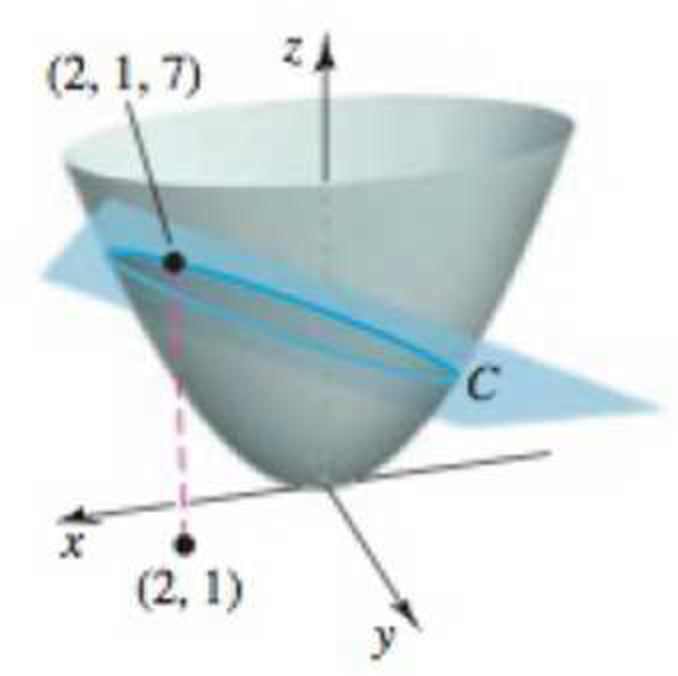
Line tangent to an intersection curve Consider the paraboloid z = x2 + 3y2 and the plane z = x + y + 4, which intersects the paraboloid in a curve C at (2, 1, 7) (see figure). Find the equation of the line tangent to C at the point (2.1, 7). Proceed as follows.
a. Find a vector normal to the plane at (2, 1, 7).
b. Find a vector normal to the plane tangent to the paraboloid at (2,1,7).
c. Argue that the line tangent to C at (2, 1, 7) is orthogonal to both normal
d. Knowing a point on the tangent line and the direction of the tangent line, write an equation of the tangent line in parametric form.
Want to see the full answer?
Check out a sample textbook solution
Chapter 15 Solutions
CALCULUS:EARLY TRANSCENDENTALS-PACKAGE
Additional Math Textbook Solutions
Calculus for Business, Economics, Life Sciences, and Social Sciences (14th Edition)
Algebra and Trigonometry (6th Edition)
Pre-Algebra Student Edition
Elementary Statistics: Picturing the World (7th Edition)
Elementary Statistics (13th Edition)
- Complete the description of the piecewise function graphed below. Use interval notation to indicate the intervals. -7 -6 -5 -4 30 6 5 4 3 0 2 1 -1 5 6 + -2 -3 -5 456 -6 - { 1 if x Є f(x) = { 1 if x Є { 3 if x Єarrow_forwardComplete the description of the piecewise function graphed below. 6 5 -7-6-5-4-3-2-1 2 3 5 6 -1 -2 -3 -4 -5 { f(x) = { { -6 if -6x-2 if -2< x <1 if 1 < x <6arrow_forwardLet F = V where (x, y, z) x2 1 + sin² 2 +z2 and let A be the line integral of F along the curve x = tcost, y = t sint, z=t, starting on the plane z = 6.14 and ending on the plane z = 4.30. Then sin(3A) is -0.598 -0.649 0.767 0.278 0.502 0.010 -0.548 0.960arrow_forward
- Let C be the intersection of the cylinder x² + y² = 2.95 with the plane z = 1.13x, with the clockwise orientation, as viewed from above. Then the value of cos (₤23 COS 2 y dx xdy+3 z dzis 3 z dz) is 0.131 -0.108 -0.891 -0.663 -0.428 0.561 -0.332 -0.387arrow_forward2 x² + 47 The partial fraction decomposition of f(x) g(x) can be written in the form of + x3 + 4x2 2 C I where f(x) = g(x) h(x) = h(x) + x +4arrow_forwardThe partial fraction decomposition of f(x) 4x 7 g(x) + where 3x4 f(x) = g(x) = - 52 –10 12x237x+28 can be written in the form ofarrow_forward
- 1. Sketch the following piecewise function on the graph. (5 points) x<-1 3 x² -1≤ x ≤2 f(x) = = 1 ४ | N 2 x ≥ 2 -4- 3 2 -1- -4 -3 -2 -1 0 1 -1- --2- -3- -4- -N 2 3 4arrow_forward2. Let f(x) = 2x² + 6. Find and completely simplify the rate of change on the interval [3,3+h]. (5 points)arrow_forward(x)=2x-x2 2 a=2, b = 1/2, C=0 b) Vertex v F(x)=ax 2 + bx + c x= Za V=2.0L YEF(- =) = 4 b (글) JANUARY 17, 2025 WORKSHEET 1 Solve the following four problems on a separate sheet. Fully justify your answers to MATH 122 ล T earn full credit. 1. Let f(x) = 2x- 1x2 2 (a) Rewrite this quadratic function in standard form: f(x) = ax² + bx + c and indicate the values of the coefficients: a, b and c. (b) Find the vertex V, focus F, focal width, directrix D, and the axis of symmetry for the graph of y = f(x). (c) Plot a graph of y = f(x) and indicate all quantities found in part (b) on your graph. (d) Specify the domain and range of the function f. OUR 2. Let g(x) = f(x) u(x) where f is the quadratic function from problem 1 and u is the unit step function: u(x) = { 0 1 if x ≥0 0 if x<0 y = u(x) 0 (a) Write a piecewise formula for the function g. (b) Sketch a graph of y = g(x). (c) Indicate the domain and range of the function g. X фирм where u is the unit step function defined in problem 2. 3. Let…arrow_forward
- Question 1arrow_forward"P3 Question 3: Construct the accessibility matrix Passociated with the following graphs, and compute P2 and identify each at the various two-step paths in the graph Ps P₁ P₂arrow_forwardA cable television company estimates that with x thousand subscribers, its monthly revenue and cost (in thousands of dollars) are given by the following equations. R(x) = 45x - 0.24x2 C(x) = 257 + 13xarrow_forward
 Algebra and Trigonometry (MindTap Course List)AlgebraISBN:9781305071742Author:James Stewart, Lothar Redlin, Saleem WatsonPublisher:Cengage LearningAlgebra & Trigonometry with Analytic GeometryAlgebraISBN:9781133382119Author:SwokowskiPublisher:Cengage
Algebra and Trigonometry (MindTap Course List)AlgebraISBN:9781305071742Author:James Stewart, Lothar Redlin, Saleem WatsonPublisher:Cengage LearningAlgebra & Trigonometry with Analytic GeometryAlgebraISBN:9781133382119Author:SwokowskiPublisher:Cengage Elementary Geometry For College Students, 7eGeometryISBN:9781337614085Author:Alexander, Daniel C.; Koeberlein, Geralyn M.Publisher:Cengage,
Elementary Geometry For College Students, 7eGeometryISBN:9781337614085Author:Alexander, Daniel C.; Koeberlein, Geralyn M.Publisher:Cengage, Trigonometry (MindTap Course List)TrigonometryISBN:9781337278461Author:Ron LarsonPublisher:Cengage Learning
Trigonometry (MindTap Course List)TrigonometryISBN:9781337278461Author:Ron LarsonPublisher:Cengage Learning Elementary Linear Algebra (MindTap Course List)AlgebraISBN:9781305658004Author:Ron LarsonPublisher:Cengage Learning
Elementary Linear Algebra (MindTap Course List)AlgebraISBN:9781305658004Author:Ron LarsonPublisher:Cengage Learning




