Chapter 1.5, Problem 45E

Solution

(a)

To find: The inverse of the function $f(x)$ is continuous..

The inverse of the function is continuous.

Given information

If a one-to-one function is continuous in its domain, then its inverse function is also continuous.

We can prove it by an example let $f(x)=x^3+2$ and the inverse of f(x) is $g(x)={\left(x-2\right)}^{\frac{1}{3}}$ The graph of f(x) and g(x) are given below.

  

It can be seen that both f(x) and g(x) are continuous. The graph of $f$ is reflected in an imaginary mirror along the line y=x to produce the graph of $f^{-1}(x)$

(b)

To find: The inverse of the function $f(x)$ is one one.

The inverse of the function is is one one.

Given information

We can prove it by an example let $f(x)=x^3+2$ and the inverse of f(x) is $g(x)={\left(x-2\right)}^{\frac{1}{3}}$ The graph of f(x) and g(x) are given below.

  

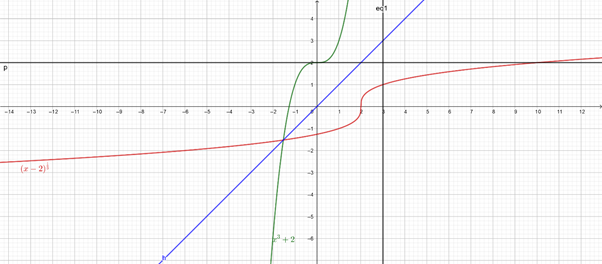
The inverse of the function passes the vertical and horizontal line test so it is one − one.

(c)

To find: The inverse of the function $f(x)$ is odd..

The inverse of the function is odd.

Given information

If a one-to-one function is continuous in its domain, then its inverse function is also continuous.

We can prove it by an example let $f(x)=x^3+2$ and the inverse of f(x) is $g(x)={\left(x-2\right)}^{\frac{1}{3}}$ The graph of f(x) and g(x) are given below.

  

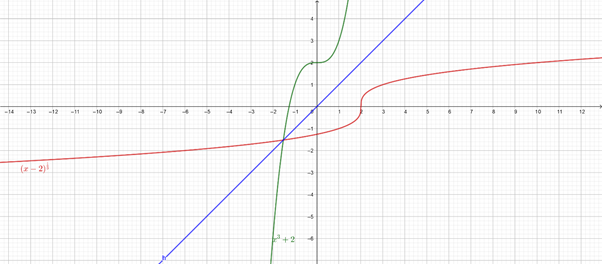
As it is clear from the graph that inverse of f(x) is symmetrical about the origin and it is odd therefore $f^{-1}$ is also odd.

(d)

To find: The inverse of the function $f(x)$ is increasing.

The inverse of the function is increasing.

Given information

If a one-to-one function is continuous in its domain, then its inverse function is also continuous.

We can prove it by an example let $f(x)=x^3+2$ and the inverse of f(x) is $g(x)={\left(x-2\right)}^{\frac{1}{3}}$

It is clear from the graph for $x_2>x_1$ so $f(x_2)>f(x_1)$

Hence $f(x)$ is increasing similarly in g(x) $x_2>x_1$ $g(x_2)>g(x_1)$ it is also increasing.