10th Edition

ISBN: 9780134781839

Author: Demana

Publisher: PEARSON

Concept explainers

The word “unitary” comes from the word “unit”, which means a single and complete entity. In this method, we find the value of a unit product from the given number of products, and then we solve for the other number of products.

Speed, Time, and Distance

Imagine you and 3 of your friends are planning to go to the playground at 6 in the evening. Your house is one mile away from the playground and one of your friends named Jim must start at 5 pm to reach the playground by walk. The other two friends are 3 …

Profit and Loss

The amount earned or lost on the sale of one or more items is referred to as the profit or loss on that item.

Units and Measurements

Measurements and comparisons are the foundation of science and engineering. We, therefore, need rules that tell us how things are measured and compared. For these measurements and comparisons, we perform certain experiments, and we will need the experime…

Videos

Expert Solution & Answer

Chapter 1.5, Problem 23E

Solution

To determine that the given function is one-to-one and sketch the inverse of the function if it is one-to-one.

Yes, the given function is one-to-one.

Given : The sketch of the given function is:

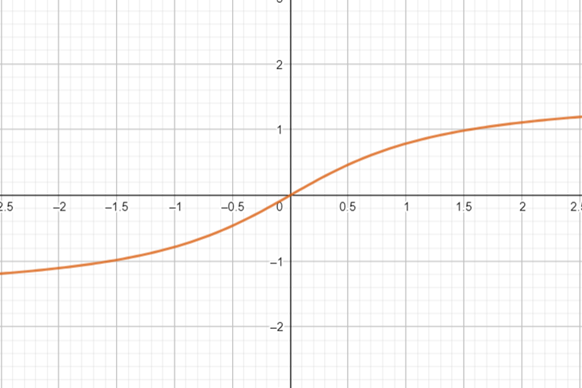
Information: A function y=f(x) is said to be one-to-one, if no two values of x gives the same value of y . For each value of y in the range of f(x) , there would be exactly only one value of x for one-to-one function.

A horizontal line test can be used to determine whether a function is one-to-one or not. If each horizontal line y=a, a∈R intersects the graph in at most one point. In other words, the horizontal line should not intersect the graph at more than one point, then function is said to be one-to-one.

A function f(x) and its inverse function f−1(x) are the reflections about the line y=x. Hence, the inverse of a function f(x) can be sketched using the reflection of the function about the line y=x.

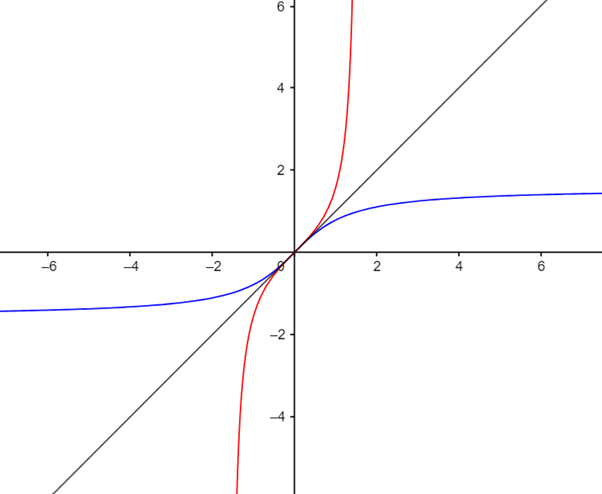
Interpretation: For the above graph, the graph does not intersect any horizontal line at more than one point. Hence, the function is one-to-one. The inverse of given function is sketched using the reflection of the function about the line y=x. The blue curve represents the sketch of the given function and the red curve represents the sketch of the inverse. The green curve is the line y=x.

Graph:

Chapter 1.5, Problem 22E

Chapter 1.5, Problem 24E

Chapter 1 Solutions

PRECALCULUS:...COMMON CORE ED.-W/ACCESS

Ch. 1.1 - Prob. 1QR Ch. 1.1 - Prob. 2QR Ch. 1.1 - Prob. 3QR Ch. 1.1 - Prob. 4QR Ch. 1.1 - Prob. 5QR Ch. 1.1 - Prob. 6QR Ch. 1.1 - Prob. 7QR Ch. 1.1 - Prob. 8QR Ch. 1.1 - Prob. 9QR Ch. 1.1 - Prob. 10QR

Ch. 1.1 - Prob. 1E Ch. 1.1 - Prob. 2E Ch. 1.1 - Prob. 3E Ch. 1.1 - Prob. 4E Ch. 1.1 - Prob. 5E Ch. 1.1 - Prob. 6E Ch. 1.1 - Prob. 7E Ch. 1.1 - Prob. 8E Ch. 1.1 - Prob. 9E Ch. 1.1 - Prob. 10E Ch. 1.1 - Prob. 11E Ch. 1.1 - Prob. 12E Ch. 1.1 - Prob. 13E Ch. 1.1 - Prob. 14E Ch. 1.1 - Prob. 15E Ch. 1.1 - Prob. 16E Ch. 1.1 - Prob. 18E Ch. 1.1 - Prob. 19E Ch. 1.1 - Prob. 20E Ch. 1.1 - Prob. 21E Ch. 1.1 - Prob. 22E Ch. 1.1 - Prob. 23E Ch. 1.1 - Prob. 24E Ch. 1.1 - Prob. 25E Ch. 1.1 - Prob. 26E Ch. 1.1 - Prob. 27E Ch. 1.1 - Prob. 28E Ch. 1.1 - Prob. 29E Ch. 1.1 - Prob. 30E Ch. 1.1 - Prob. 31E Ch. 1.1 - Prob. 32E Ch. 1.1 - Prob. 33E Ch. 1.1 - Prob. 34E Ch. 1.1 - Prob. 35E Ch. 1.1 - Prob. 36E Ch. 1.1 - Prob. 37E Ch. 1.1 - Prob. 38E Ch. 1.1 - Prob. 39E Ch. 1.1 - Prob. 40E Ch. 1.1 - Prob. 41E Ch. 1.1 - Prob. 42E Ch. 1.1 - Prob. 43E Ch. 1.1 - Prob. 44E Ch. 1.1 - Prob. 45E Ch. 1.1 - Prob. 46E Ch. 1.1 - Prob. 47E Ch. 1.1 - Prob. 48E Ch. 1.1 - Prob. 49E Ch. 1.1 - Prob. 50E Ch. 1.1 - Prob. 51E Ch. 1.1 - Prob. 52E Ch. 1.1 - Prob. 53E Ch. 1.1 - Prob. 54E Ch. 1.1 - Prob. 55E Ch. 1.1 - Prob. 56E Ch. 1.1 - Prob. 57E Ch. 1.1 - Prob. 58E Ch. 1.1 - Prob. 59E Ch. 1.1 - Prob. 60E Ch. 1.1 - Prob. 61E Ch. 1.1 - Prob. 62E Ch. 1.1 - Prob. 63E Ch. 1.2 - Prob. 1QR Ch. 1.2 - Prob. 2QR Ch. 1.2 - Prob. 3QR Ch. 1.2 - Prob. 4QR Ch. 1.2 - Prob. 5QR Ch. 1.2 - Prob. 6QR Ch. 1.2 - Prob. 7QR Ch. 1.2 - Prob. 8QR Ch. 1.2 - Prob. 9QR Ch. 1.2 - Prob. 10QR Ch. 1.2 - Prob. 1E Ch. 1.2 - Prob. 2E Ch. 1.2 - Prob. 3E Ch. 1.2 - Prob. 4E Ch. 1.2 - Prob. 5E Ch. 1.2 - Prob. 6E Ch. 1.2 - Prob. 7E Ch. 1.2 - Prob. 8E Ch. 1.2 - Prob. 9E Ch. 1.2 - Prob. 10E Ch. 1.2 - Prob. 11E Ch. 1.2 - Prob. 12E Ch. 1.2 - Prob. 13E Ch. 1.2 - Prob. 14E Ch. 1.2 - Prob. 15E Ch. 1.2 - Prob. 16E Ch. 1.2 - Prob. 17E Ch. 1.2 - Prob. 18E Ch. 1.2 - Prob. 19E Ch. 1.2 - Prob. 20E Ch. 1.2 - Prob. 21E Ch. 1.2 - Prob. 22E Ch. 1.2 - Prob. 23E Ch. 1.2 - Prob. 24E Ch. 1.2 - Prob. 25E Ch. 1.2 - Prob. 26E Ch. 1.2 - Prob. 27E Ch. 1.2 - Prob. 28E Ch. 1.2 - Prob. 29E Ch. 1.2 - Prob. 30E Ch. 1.2 - Prob. 31E Ch. 1.2 - Prob. 32E Ch. 1.2 - Prob. 33E Ch. 1.2 - Prob. 34E Ch. 1.2 - Prob. 35E Ch. 1.2 - Prob. 36E Ch. 1.2 - Prob. 37E Ch. 1.2 - Prob. 38E Ch. 1.2 - Prob. 39E Ch. 1.2 - Prob. 40E Ch. 1.2 - Prob. 41E Ch. 1.2 - Prob. 42E Ch. 1.2 - Prob. 43E Ch. 1.2 - Prob. 44E Ch. 1.2 - Prob. 45E Ch. 1.2 - Prob. 46E Ch. 1.2 - Prob. 47E Ch. 1.2 - Prob. 48E Ch. 1.2 - Prob. 49E Ch. 1.2 - Prob. 50E Ch. 1.2 - Prob. 51E Ch. 1.2 - Prob. 52E Ch. 1.2 - Prob. 53E Ch. 1.2 - Prob. 54E Ch. 1.2 - Prob. 55E Ch. 1.2 - Prob. 56E Ch. 1.2 - Prob. 57E Ch. 1.2 - Prob. 58E Ch. 1.2 - Prob. 59E Ch. 1.2 - Prob. 60E Ch. 1.2 - Prob. 61E Ch. 1.2 - Prob. 62E Ch. 1.2 - Prob. 63E Ch. 1.2 - Prob. 64E Ch. 1.2 - Prob. 65E Ch. 1.2 - Prob. 66E Ch. 1.2 - Prob. 67E Ch. 1.2 - Prob. 68E Ch. 1.2 - Prob. 69E Ch. 1.2 - Prob. 70E Ch. 1.2 - Prob. 71E Ch. 1.2 - Prob. 72E Ch. 1.2 - Prob. 73E Ch. 1.2 - Prob. 74E Ch. 1.2 - Prob. 75E Ch. 1.2 - Prob. 76E Ch. 1.2 - Prob. 77E Ch. 1.2 - Prob. 78E Ch. 1.2 - Prob. 79E Ch. 1.2 - Prob. 80E Ch. 1.2 - Prob. 81E Ch. 1.2 - Prob. 82E Ch. 1.2 - Prob. 83E Ch. 1.2 - Prob. 84E Ch. 1.2 - Prob. 85E Ch. 1.2 - Prob. 86E Ch. 1.2 - Prob. 87E Ch. 1.3 - Prob. 1QR Ch. 1.3 - In Exercises 110, evaluate the expression without...Ch. 1.3 - In Exercises 110, evaluate the expression without...Ch. 1.3 - Prob. 4QR Ch. 1.3 - In Exercises 110, evaluate the expression without...Ch. 1.3 - Prob. 6QR Ch. 1.3 - Prob. 7QR Ch. 1.3 - Prob. 8QR Ch. 1.3 - Prob. 9QR Ch. 1.3 - Prob. 10QR Ch. 1.3 - Prob. 1E Ch. 1.3 - Prob. 2E Ch. 1.3 - In Exercises 112, each graph is a slight variation...Ch. 1.3 - Prob. 4E Ch. 1.3 - Prob. 5E Ch. 1.3 - Prob. 6E Ch. 1.3 - Prob. 7E Ch. 1.3 - Prob. 8E Ch. 1.3 - Prob. 9E Ch. 1.3 - Prob. 10E Ch. 1.3 - Prob. 11E Ch. 1.3 - Prob. 12E Ch. 1.3 - Prob. 13E Ch. 1.3 - Prob. 14E Ch. 1.3 - Prob. 15E Ch. 1.3 - Prob. 16E Ch. 1.3 - Prob. 17E Ch. 1.3 - Prob. 18E Ch. 1.3 - Prob. 19E Ch. 1.3 - Prob. 20E Ch. 1.3 - Prob. 21E Ch. 1.3 - Prob. 22E Ch. 1.3 - Prob. 23E Ch. 1.3 - Prob. 24E Ch. 1.3 - Prob. 25E Ch. 1.3 - Prob. 26E Ch. 1.3 - Prob. 27E Ch. 1.3 - Prob. 28E Ch. 1.3 - Prob. 29E Ch. 1.3 - Prob. 30E Ch. 1.3 - Prob. 31E Ch. 1.3 - Prob. 32E Ch. 1.3 - Prob. 33E Ch. 1.3 - Prob. 34E Ch. 1.3 - Prob. 35E Ch. 1.3 - Prob. 36E Ch. 1.3 - Prob. 37E Ch. 1.3 - Prob. 38E Ch. 1.3 - Prob. 39E Ch. 1.3 - Prob. 40E Ch. 1.3 - Prob. 41E Ch. 1.3 - Prob. 42E Ch. 1.3 - Prob. 43E Ch. 1.3 - Prob. 44E Ch. 1.3 - Prob. 45E Ch. 1.3 - Prob. 46E Ch. 1.3 - Prob. 47E Ch. 1.3 - Prob. 48E Ch. 1.3 - Prob. 49E Ch. 1.3 - Prob. 50E Ch. 1.3 - Prob. 51E Ch. 1.3 - Prob. 52E Ch. 1.3 - Prob. 53E Ch. 1.3 - Prob. 54E Ch. 1.3 - Prob. 55E Ch. 1.3 - Prob. 56E Ch. 1.3 - Prob. 57E Ch. 1.3 - Prob. 58E Ch. 1.3 - Prob. 59E Ch. 1.3 - Prob. 60E Ch. 1.3 - Prob. 61E Ch. 1.3 - Prob. 62E Ch. 1.3 - Prob. 63E Ch. 1.3 - Prob. 64E Ch. 1.3 - Prob. 65E Ch. 1.3 - Prob. 67E Ch. 1.3 - Prob. 68E Ch. 1.3 - Prob. 69E Ch. 1.4 - Prob. 1QR Ch. 1.4 - Prob. 2QR Ch. 1.4 - Prob. 3QR Ch. 1.4 - Prob. 4QR Ch. 1.4 - Prob. 5QR Ch. 1.4 - Prob. 6QR Ch. 1.4 - Prob. 7QR Ch. 1.4 - Prob. 8QR Ch. 1.4 - Prob. 9QR Ch. 1.4 - Prob. 10QR Ch. 1.4 - In Exercises 14 find formulas for the functions...Ch. 1.4 - In Exercises 14 find formulas for the functions...Ch. 1.4 - Prob. 3E Ch. 1.4 - Prob. 4E Ch. 1.4 - Prob. 5E Ch. 1.4 - Prob. 6E Ch. 1.4 - Prob. 7E Ch. 1.4 - Prob. 8E Ch. 1.4 - Prob. 9E Ch. 1.4 - Prob. 10E Ch. 1.4 - Prob. 11E Ch. 1.4 - Prob. 12E Ch. 1.4 - Prob. 13E Ch. 1.4 - Prob. 14E Ch. 1.4 - Prob. 15E Ch. 1.4 - Prob. 16E Ch. 1.4 - Prob. 17E Ch. 1.4 - Prob. 18E Ch. 1.4 - Prob. 19E Ch. 1.4 - Prob. 20E Ch. 1.4 - Prob. 21E Ch. 1.4 - Prob. 22E Ch. 1.4 - Prob. 23E Ch. 1.4 - Prob. 24E Ch. 1.4 - Prob. 25E Ch. 1.4 - Prob. 26E Ch. 1.4 - Prob. 27E Ch. 1.4 - Prob. 28E Ch. 1.4 - Prob. 29E Ch. 1.4 - Prob. 30E Ch. 1.4 - Prob. 31E Ch. 1.4 - Prob. 32E Ch. 1.4 - Prob. 33E Ch. 1.4 - Prob. 34E Ch. 1.4 - Prob. 35E Ch. 1.4 - Prob. 36E Ch. 1.4 - Prob. 37E Ch. 1.4 - Prob. 38E Ch. 1.4 - Prob. 39E Ch. 1.4 - Prob. 40E Ch. 1.4 - Prob. 41E Ch. 1.4 - Prob. 42E Ch. 1.4 - Prob. 43E Ch. 1.4 - Prob. 44E Ch. 1.4 - Prob. 45E Ch. 1.4 - Prob. 46E Ch. 1.4 - Prob. 47E Ch. 1.4 - Prob. 48E Ch. 1.4 - Prob. 49E Ch. 1.4 - Prob. 50E Ch. 1.4 - Prob. 51E Ch. 1.4 - Prob. 52E Ch. 1.4 - Prob. 53E Ch. 1.4 - Prob. 54E Ch. 1.4 - Prob. 55E Ch. 1.5 - Prob. 1QR Ch. 1.5 - Prob. 2QR Ch. 1.5 - Prob. 3QR Ch. 1.5 - Prob. 4QR Ch. 1.5 - Prob. 5QR Ch. 1.5 - Prob. 6QR Ch. 1.5 - Prob. 7QR Ch. 1.5 - Prob. 8QR Ch. 1.5 - Prob. 9QR Ch. 1.5 - Prob. 10QR Ch. 1.5 - Prob. 1E Ch. 1.5 - Prob. 2E Ch. 1.5 - Prob. 3E Ch. 1.5 - Prob. 4E Ch. 1.5 - Prob. 5E Ch. 1.5 - Prob. 6E Ch. 1.5 - Prob. 7E Ch. 1.5 - Prob. 8E Ch. 1.5 - Prob. 9E Ch. 1.5 - Prob. 10E Ch. 1.5 - Prob. 11E Ch. 1.5 - Prob. 12E Ch. 1.5 - Prob. 13E Ch. 1.5 - In Exercises 1322, find a formula for f1x . Give...Ch. 1.5 - Prob. 15E Ch. 1.5 - Prob. 16E Ch. 1.5 - Prob. 17E Ch. 1.5 - Prob. 18E Ch. 1.5 - Prob. 19E Ch. 1.5 - Prob. 20E Ch. 1.5 - Prob. 21E Ch. 1.5 - Prob. 22E Ch. 1.5 - Prob. 23E Ch. 1.5 - Prob. 24E Ch. 1.5 - Prob. 25E Ch. 1.5 - Prob. 26E Ch. 1.5 - Prob. 27E Ch. 1.5 - Prob. 28E Ch. 1.5 - Prob. 29E Ch. 1.5 - Prob. 30E Ch. 1.5 - Prob. 31E Ch. 1.5 - Prob. 32E Ch. 1.5 - Prob. 33E Ch. 1.5 - Prob. 34E Ch. 1.5 - Prob. 35E Ch. 1.5 - Prob. 36E Ch. 1.5 - Prob. 37E Ch. 1.5 - Prob. 38E Ch. 1.5 - Prob. 39E Ch. 1.5 - Prob. 40E Ch. 1.5 - Prob. 41E Ch. 1.5 - Prob. 42E Ch. 1.5 - Prob. 43E Ch. 1.5 - Prob. 44E Ch. 1.5 - Prob. 45E Ch. 1.5 - Prob. 46E Ch. 1.5 - Prob. 47E Ch. 1.5 - Prob. 48E Ch. 1.5 - Prob. 49E Ch. 1.5 - Prob. 50E Ch. 1.5 - Prob. 51E Ch. 1.6 - Prob. 1QR Ch. 1.6 - Prob. 2QR Ch. 1.6 - Prob. 3QR Ch. 1.6 - Prob. 4QR Ch. 1.6 - Prob. 5QR Ch. 1.6 - Prob. 6QR Ch. 1.6 - Prob. 7QR Ch. 1.6 - Prob. 8QR Ch. 1.6 - Prob. 9QR Ch. 1.6 - Prob. 10QR Ch. 1.6 - Prob. 1E Ch. 1.6 - Prob. 2E Ch. 1.6 - Prob. 3E Ch. 1.6 - Prob. 4E Ch. 1.6 - Prob. 5E Ch. 1.6 - Prob. 6E Ch. 1.6 - Prob. 7E Ch. 1.6 - Prob. 8E Ch. 1.6 - Prob. 9E Ch. 1.6 - Prob. 10E Ch. 1.6 - Prob. 11E Ch. 1.6 - Prob. 12E Ch. 1.6 - Prob. 13E Ch. 1.6 - Prob. 14E Ch. 1.6 - Prob. 15E Ch. 1.6 - Prob. 16E Ch. 1.6 - Prob. 17E Ch. 1.6 - Prob. 18E Ch. 1.6 - Prob. 19E Ch. 1.6 - Prob. 20E Ch. 1.6 - Prob. 21E Ch. 1.6 - Prob. 22E Ch. 1.6 - Prob. 23E Ch. 1.6 - Prob. 24E Ch. 1.6 - Prob. 25E Ch. 1.6 - Prob. 26E Ch. 1.6 - Prob. 27E Ch. 1.6 - Prob. 28E Ch. 1.6 - Prob. 29E Ch. 1.6 - Prob. 30E Ch. 1.6 - Prob. 31E Ch. 1.6 - Prob. 32E Ch. 1.6 - Prob. 33E Ch. 1.6 - Prob. 34E Ch. 1.6 - Prob. 35E Ch. 1.6 - Prob. 36E Ch. 1.6 - Prob. 37E Ch. 1.6 - Prob. 38E Ch. 1.6 - Prob. 39E Ch. 1.6 - Prob. 40E Ch. 1.6 - Prob. 41E Ch. 1.6 - Prob. 42E Ch. 1.6 - Prob. 43E Ch. 1.6 - Prob. 44E Ch. 1.6 - Prob. 45E Ch. 1.6 - Prob. 46E Ch. 1.6 - Prob. 47E Ch. 1.6 - Prob. 48E Ch. 1.6 - Prob. 49E Ch. 1.6 - Prob. 50E Ch. 1.6 - Prob. 51E Ch. 1.6 - Prob. 52E Ch. 1.6 - Prob. 53E Ch. 1.6 - Prob. 54E Ch. 1.6 - Prob. 55E Ch. 1.6 - Prob. 56E Ch. 1.6 - Prob. 57E Ch. 1.6 - Prob. 58E Ch. 1.6 - Prob. 59E Ch. 1.6 - Prob. 60E Ch. 1.6 - Prob. 61E Ch. 1.6 - Prob. 62E Ch. 1.6 - Prob. 63E Ch. 1.6 - Prob. 64E Ch. 1.6 - Prob. 65E Ch. 1.6 - Prob. 66E Ch. 1.6 - Prob. 67E Ch. 1.6 - Prob. 68E Ch. 1.7 - Prob. 1QR Ch. 1.7 - Prob. 2QR Ch. 1.7 - Prob. 3QR Ch. 1.7 - Prob. 4QR Ch. 1.7 - Prob. 5QR Ch. 1.7 - Prob. 6QR Ch. 1.7 - Prob. 7QR Ch. 1.7 - Prob. 8QR Ch. 1.7 - Prob. 9QR Ch. 1.7 - Prob. 10QR Ch. 1.7 - Prob. 1E Ch. 1.7 - Prob. 2E Ch. 1.7 - Prob. 3E Ch. 1.7 - Prob. 4E Ch. 1.7 - Prob. 5E Ch. 1.7 - Prob. 6E Ch. 1.7 - Prob. 7E Ch. 1.7 - Prob. 8E Ch. 1.7 - In Exercises 110, write a mathematical expression...Ch. 1.7 - Prob. 10E Ch. 1.7 - Prob. 11E Ch. 1.7 - Prob. 12E Ch. 1.7 - Prob. 13E Ch. 1.7 - In Exercises 1114, choose a variable and write a...Ch. 1.7 - Prob. 15E Ch. 1.7 - In Exercises 1520, write the specified quantity as...Ch. 1.7 - Prob. 17E Ch. 1.7 - Prob. 18E Ch. 1.7 - Prob. 19E Ch. 1.7 - Prob. 20E Ch. 1.7 - Prob. 21E Ch. 1.7 - Prob. 22E Ch. 1.7 - Prob. 23E Ch. 1.7 - Prob. 24E Ch. 1.7 - Prob. 25E Ch. 1.7 - Prob. 26E Ch. 1.7 - Prob. 27E Ch. 1.7 - Prob. 28E Ch. 1.7 - Prob. 29E Ch. 1.7 - Prob. 30E Ch. 1.7 - Prob. 31E Ch. 1.7 - Prob. 32E Ch. 1.7 - Prob. 33E Ch. 1.7 - Prob. 34E Ch. 1.7 - Prob. 35E Ch. 1.7 - In Exercises 2136, write an equation for the...Ch. 1.7 - Finding the Model and Solving Water is stored in a...Ch. 1.7 - Prob. 38E Ch. 1.7 - Prob. 39E Ch. 1.7 - Prob. 40E Ch. 1.7 - Prob. 41E Ch. 1.7 - Prob. 42E Ch. 1.7 - Prob. 43E Ch. 1.7 - Prob. 44E Ch. 1.7 - Prob. 45E Ch. 1.7 - Prob. 46E Ch. 1.7 - Prob. 47E Ch. 1.7 - Prob. 48E Ch. 1.7 - Prob. 49E Ch. 1.7 - Prob. 50E Ch. 1.7 - Prob. 51E Ch. 1 - Prob. 1RE Ch. 1 - Prob. 2RE Ch. 1 - Prob. 3RE Ch. 1 - Prob. 4RE Ch. 1 - Prob. 5RE Ch. 1 - Prob. 6RE Ch. 1 - Prob. 7RE Ch. 1 - Prob. 8RE Ch. 1 - Prob. 9RE Ch. 1 - Prob. 10RE Ch. 1 - Prob. 11RE Ch. 1 - Prob. 12RE Ch. 1 - Prob. 13RE Ch. 1 - Prob. 14RE Ch. 1 - Prob. 15RE Ch. 1 - Prob. 16RE Ch. 1 - Prob. 17RE Ch. 1 - Prob. 18RE Ch. 1 - Prob. 19RE Ch. 1 - Prob. 20RE Ch. 1 - Prob. 21RE Ch. 1 - Prob. 22RE Ch. 1 - Prob. 23RE Ch. 1 - Prob. 24RE Ch. 1 - Prob. 25RE Ch. 1 - Prob. 26RE Ch. 1 - Prob. 27RE Ch. 1 - Prob. 28RE Ch. 1 - Prob. 29RE Ch. 1 - Prob. 30RE Ch. 1 - Prob. 31RE Ch. 1 - Prob. 32RE Ch. 1 - Prob. 33RE Ch. 1 - Prob. 34RE Ch. 1 - Prob. 35RE Ch. 1 - Prob. 36RE Ch. 1 - Prob. 37RE Ch. 1 - Prob. 38RE Ch. 1 - Prob. 39RE Ch. 1 - Prob. 40RE Ch. 1 - Prob. 41RE Ch. 1 - Prob. 42RE Ch. 1 - Prob. 43RE Ch. 1 - Prob. 44RE Ch. 1 - Prob. 45RE Ch. 1 - Prob. 46RE Ch. 1 - Prob. 47RE Ch. 1 - Prob. 48RE Ch. 1 - Prob. 49RE Ch. 1 - Prob. 50RE Ch. 1 - Prob. 51RE Ch. 1 - Prob. 52RE Ch. 1 - Prob. 53RE Ch. 1 - Prob. 54RE Ch. 1 - Prob. 55RE Ch. 1 - Prob. 56RE Ch. 1 - Prob. 57RE Ch. 1 - Prob. 58RE Ch. 1 - Prob. 59RE Ch. 1 - Prob. 60RE Ch. 1 - In Exercises 5964, write the specified quantity as...Ch. 1 - Prob. 62RE Ch. 1 - Prob. 63RE Ch. 1 - Prob. 64RE Ch. 1 - Prob. 65RE Ch. 1 - Prob. 67RE Ch. 1 - Prob. 68RE

Knowledge Booster

$Calculus$

Learn more about

Need a deep-dive on the concept behind this application? Look no further. Learn more about this topic, calculus and related others by exploring similar questions and additional content below.

Recommended textbooks for you

Calculus: Early Transcendentals
Calculus
ISBN:9781285741550
Author:James Stewart
Publisher:Cengage Learning
Thomas' Calculus (14th Edition)
Calculus
ISBN:9780134438986
Author:Joel R. Hass, Christopher E. Heil, Maurice D. Weir
Publisher:PEARSON
Calculus: Early Transcendentals (3rd Edition)
Calculus
ISBN:9780134763644
Author:William L. Briggs, Lyle Cochran, Bernard Gillett, Eric Schulz
Publisher:PEARSON
Calculus: Early Transcendentals
Calculus
ISBN:9781319050740
Author:Jon Rogawski, Colin Adams, Robert Franzosa
Publisher:W. H. Freeman
Precalculus
Calculus
ISBN:9780135189405
Author:Michael Sullivan
Publisher:PEARSON
Calculus: Early Transcendental Functions
Calculus
ISBN:9781337552516
Author:Ron Larson, Bruce H. Edwards
Publisher:Cengage Learning

Calculus: Early Transcendentals

Calculus

ISBN:9781285741550

Author:James Stewart

Publisher:Cengage Learning

Thomas' Calculus (14th Edition)

Calculus

ISBN:9780134438986

Author:Joel R. Hass, Christopher E. Heil, Maurice D. Weir

Publisher:PEARSON

Calculus: Early Transcendentals (3rd Edition)

Calculus

ISBN:9780134763644

Author:William L. Briggs, Lyle Cochran, Bernard Gillett, Eric Schulz

Publisher:PEARSON

Calculus: Early Transcendentals

Calculus

ISBN:9781319050740

Author:Jon Rogawski, Colin Adams, Robert Franzosa

Publisher:W. H. Freeman

Precalculus

Calculus

ISBN:9780135189405

Author:Michael Sullivan

Publisher:PEARSON

Calculus: Early Transcendental Functions

Calculus

ISBN:9781337552516

Author:Ron Larson, Bruce H. Edwards

Publisher:Cengage Learning

SEE MORE TEXTBOOKS

Use of ALGEBRA in REAL LIFE; Author: Fast and Easy Maths !;https://www.youtube.com/watch?v=9_PbWFpvkDc;License: Standard YouTube License, CC-BY

Compound Interest Formula Explained, Investment, Monthly & Continuously, Word Problems, Algebra; Author: The Organic Chemistry Tutor;https://www.youtube.com/watch?v=P182Abv3fOk;License: Standard YouTube License, CC-BY

Applications of Algebra (Digit, Age, Work, Clock, Mixture and Rate Problems); Author: EngineerProf PH;https://www.youtube.com/watch?v=Y8aJ_wYCS2g;License: Standard YouTube License, CC-BY

Solution Summary: The author explains that a function is one-to-one, if no two values of x give the same value. A horizontal line test can be used to determine whether it's one to one.

Concept explainers

Videos

Chapter 1 Solutions