PRECALCULUS:...COMMON CORE ED.-W/ACCESS
PRECALCULUS:...COMMON CORE ED.-W/ACCESS
10th Edition
ISBN: 9780134781839
Author: Demana
Publisher: PEARSON
bartleby

Concept explainers

Equations and Inequations
Equations and inequalities describe the relationship between two mathematical expressions.
Linear Functions
A linear function can just be a constant, or it can be the constant multiplied with the variable like x or y. If the variables are of the form, x2, x1/2 or y2 it is not linear. The exponent over the variables should always be 1.
bartleby

Videos

Expert Solution & Answer
Book Icon
Chapter 1, Problem 33RE
Solution

To draw the graph of the given function and determine the relative maximum points.

No, relative maximum point exists.

Given information :  The given function is f(x)=(x+1)2−7 .

  PRECALCULUS:...COMMON CORE ED.-W/ACCESS, Chapter 1, Problem 33RE , additional homework tip 1

Graph:

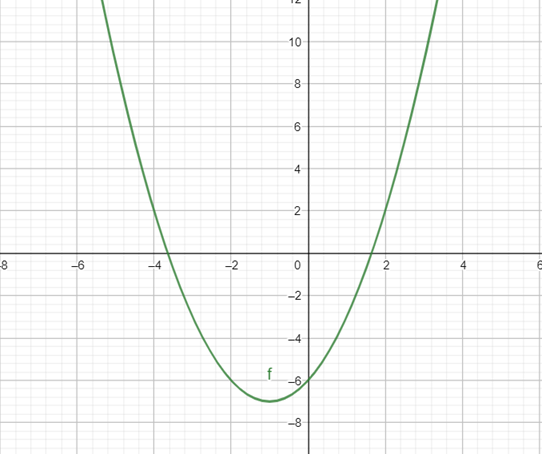
  PRECALCULUS:...COMMON CORE ED.-W/ACCESS, Chapter 1, Problem 33RE , additional homework tip 2

Interpretation : 

The relative maximum is a point across its all nearby points, at which the function has a maximum value. From the graph, it is observed that no relative maximum point exists.

To draw the graph of the given function and determine the relative minimum points.

Relative Minimum Point: (−1,−7)

Given information :  The given function is f(x)=(x+1)2−7 .

  PRECALCULUS:...COMMON CORE ED.-W/ACCESS, Chapter 1, Problem 33RE , additional homework tip 3

Graph:

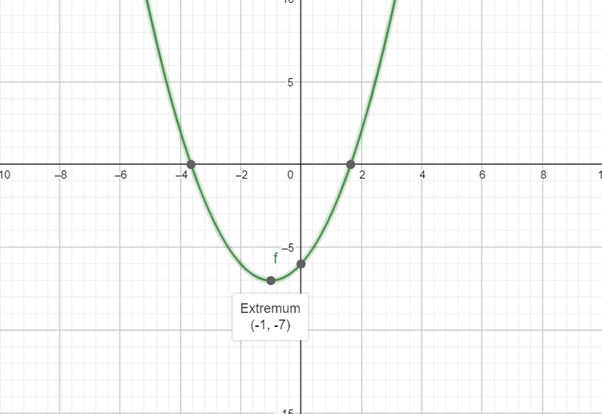
  PRECALCULUS:...COMMON CORE ED.-W/ACCESS, Chapter 1, Problem 33RE , additional homework tip 4

Interpretation : 

The relative minimum is a point across its all nearby points, at which the function has a minimum value. From the graph, the relative minimum occurs at x=−1 and the relative minimum value equal to −7 .

Previous
Chapter 1, Problem 32RE
Next
Chapter 1, Problem 34RE

Chapter 1 Solutions

PRECALCULUS:...COMMON CORE ED.-W/ACCESS

Ch. 1.1 - Prob. 1QRCh. 1.1 - Prob. 2QRCh. 1.1 - Prob. 3QRCh. 1.1 - Prob. 4QRCh. 1.1 - Prob. 5QRCh. 1.1 - Prob. 6QRCh. 1.1 - Prob. 7QRCh. 1.1 - Prob. 8QRCh. 1.1 - Prob. 9QRCh. 1.1 - Prob. 10QR
Ch. 1.1 - Prob. 1ECh. 1.1 - Prob. 2ECh. 1.1 - Prob. 3ECh. 1.1 - Prob. 4ECh. 1.1 - Prob. 5ECh. 1.1 - Prob. 6ECh. 1.1 - Prob. 7ECh. 1.1 - Prob. 8ECh. 1.1 - Prob. 9ECh. 1.1 - Prob. 10ECh. 1.1 - Prob. 11ECh. 1.1 - Prob. 12ECh. 1.1 - Prob. 13ECh. 1.1 - Prob. 14ECh. 1.1 - Prob. 15ECh. 1.1 - Prob. 16ECh. 1.1 - Prob. 18ECh. 1.1 - Prob. 19ECh. 1.1 - Prob. 20ECh. 1.1 - Prob. 21ECh. 1.1 - Prob. 22ECh. 1.1 - Prob. 23ECh. 1.1 - Prob. 24ECh. 1.1 - Prob. 25ECh. 1.1 - Prob. 26ECh. 1.1 - Prob. 27ECh. 1.1 - Prob. 28ECh. 1.1 - Prob. 29ECh. 1.1 - Prob. 30ECh. 1.1 - Prob. 31ECh. 1.1 - Prob. 32ECh. 1.1 - Prob. 33ECh. 1.1 - Prob. 34ECh. 1.1 - Prob. 35ECh. 1.1 - Prob. 36ECh. 1.1 - Prob. 37ECh. 1.1 - Prob. 38ECh. 1.1 - Prob. 39ECh. 1.1 - Prob. 40ECh. 1.1 - Prob. 41ECh. 1.1 - Prob. 42ECh. 1.1 - Prob. 43ECh. 1.1 - Prob. 44ECh. 1.1 - Prob. 45ECh. 1.1 - Prob. 46ECh. 1.1 - Prob. 47ECh. 1.1 - Prob. 48ECh. 1.1 - Prob. 49ECh. 1.1 - Prob. 50ECh. 1.1 - Prob. 51ECh. 1.1 - Prob. 52ECh. 1.1 - Prob. 53ECh. 1.1 - Prob. 54ECh. 1.1 - Prob. 55ECh. 1.1 - Prob. 56ECh. 1.1 - Prob. 57ECh. 1.1 - Prob. 58ECh. 1.1 - Prob. 59ECh. 1.1 - Prob. 60ECh. 1.1 - Prob. 61ECh. 1.1 - Prob. 62ECh. 1.1 - Prob. 63ECh. 1.2 - Prob. 1QRCh. 1.2 - Prob. 2QRCh. 1.2 - Prob. 3QRCh. 1.2 - Prob. 4QRCh. 1.2 - Prob. 5QRCh. 1.2 - Prob. 6QRCh. 1.2 - Prob. 7QRCh. 1.2 - Prob. 8QRCh. 1.2 - Prob. 9QRCh. 1.2 - Prob. 10QRCh. 1.2 - Prob. 1ECh. 1.2 - Prob. 2ECh. 1.2 - Prob. 3ECh. 1.2 - Prob. 4ECh. 1.2 - Prob. 5ECh. 1.2 - Prob. 6ECh. 1.2 - Prob. 7ECh. 1.2 - Prob. 8ECh. 1.2 - Prob. 9ECh. 1.2 - Prob. 10ECh. 1.2 - Prob. 11ECh. 1.2 - Prob. 12ECh. 1.2 - Prob. 13ECh. 1.2 - Prob. 14ECh. 1.2 - Prob. 15ECh. 1.2 - Prob. 16ECh. 1.2 - Prob. 17ECh. 1.2 - Prob. 18ECh. 1.2 - Prob. 19ECh. 1.2 - Prob. 20ECh. 1.2 - Prob. 21ECh. 1.2 - Prob. 22ECh. 1.2 - Prob. 23ECh. 1.2 - Prob. 24ECh. 1.2 - Prob. 25ECh. 1.2 - Prob. 26ECh. 1.2 - Prob. 27ECh. 1.2 - Prob. 28ECh. 1.2 - Prob. 29ECh. 1.2 - Prob. 30ECh. 1.2 - Prob. 31ECh. 1.2 - Prob. 32ECh. 1.2 - Prob. 33ECh. 1.2 - Prob. 34ECh. 1.2 - Prob. 35ECh. 1.2 - Prob. 36ECh. 1.2 - Prob. 37ECh. 1.2 - Prob. 38ECh. 1.2 - Prob. 39ECh. 1.2 - Prob. 40ECh. 1.2 - Prob. 41ECh. 1.2 - Prob. 42ECh. 1.2 - Prob. 43ECh. 1.2 - Prob. 44ECh. 1.2 - Prob. 45ECh. 1.2 - Prob. 46ECh. 1.2 - Prob. 47ECh. 1.2 - Prob. 48ECh. 1.2 - Prob. 49ECh. 1.2 - Prob. 50ECh. 1.2 - Prob. 51ECh. 1.2 - Prob. 52ECh. 1.2 - Prob. 53ECh. 1.2 - Prob. 54ECh. 1.2 - Prob. 55ECh. 1.2 - Prob. 56ECh. 1.2 - Prob. 57ECh. 1.2 - Prob. 58ECh. 1.2 - Prob. 59ECh. 1.2 - Prob. 60ECh. 1.2 - Prob. 61ECh. 1.2 - Prob. 62ECh. 1.2 - Prob. 63ECh. 1.2 - Prob. 64ECh. 1.2 - Prob. 65ECh. 1.2 - Prob. 66ECh. 1.2 - Prob. 67ECh. 1.2 - Prob. 68ECh. 1.2 - Prob. 69ECh. 1.2 - Prob. 70ECh. 1.2 - Prob. 71ECh. 1.2 - Prob. 72ECh. 1.2 - Prob. 73ECh. 1.2 - Prob. 74ECh. 1.2 - Prob. 75ECh. 1.2 - Prob. 76ECh. 1.2 - Prob. 77ECh. 1.2 - Prob. 78ECh. 1.2 - Prob. 79ECh. 1.2 - Prob. 80ECh. 1.2 - Prob. 81ECh. 1.2 - Prob. 82ECh. 1.2 - Prob. 83ECh. 1.2 - Prob. 84ECh. 1.2 - Prob. 85ECh. 1.2 - Prob. 86ECh. 1.2 - Prob. 87ECh. 1.3 - Prob. 1QRCh. 1.3 - In Exercises 110, evaluate the expression without...Ch. 1.3 - In Exercises 110, evaluate the expression without...Ch. 1.3 - Prob. 4QRCh. 1.3 - In Exercises 110, evaluate the expression without...Ch. 1.3 - Prob. 6QRCh. 1.3 - Prob. 7QRCh. 1.3 - Prob. 8QRCh. 1.3 - Prob. 9QRCh. 1.3 - Prob. 10QRCh. 1.3 - Prob. 1ECh. 1.3 - Prob. 2ECh. 1.3 - In Exercises 112, each graph is a slight variation...Ch. 1.3 - Prob. 4ECh. 1.3 - Prob. 5ECh. 1.3 - Prob. 6ECh. 1.3 - Prob. 7ECh. 1.3 - Prob. 8ECh. 1.3 - Prob. 9ECh. 1.3 - Prob. 10ECh. 1.3 - Prob. 11ECh. 1.3 - Prob. 12ECh. 1.3 - Prob. 13ECh. 1.3 - Prob. 14ECh. 1.3 - Prob. 15ECh. 1.3 - Prob. 16ECh. 1.3 - Prob. 17ECh. 1.3 - Prob. 18ECh. 1.3 - Prob. 19ECh. 1.3 - Prob. 20ECh. 1.3 - Prob. 21ECh. 1.3 - Prob. 22ECh. 1.3 - Prob. 23ECh. 1.3 - Prob. 24ECh. 1.3 - Prob. 25ECh. 1.3 - Prob. 26ECh. 1.3 - Prob. 27ECh. 1.3 - Prob. 28ECh. 1.3 - Prob. 29ECh. 1.3 - Prob. 30ECh. 1.3 - Prob. 31ECh. 1.3 - Prob. 32ECh. 1.3 - Prob. 33ECh. 1.3 - Prob. 34ECh. 1.3 - Prob. 35ECh. 1.3 - Prob. 36ECh. 1.3 - Prob. 37ECh. 1.3 - Prob. 38ECh. 1.3 - Prob. 39ECh. 1.3 - Prob. 40ECh. 1.3 - Prob. 41ECh. 1.3 - Prob. 42ECh. 1.3 - Prob. 43ECh. 1.3 - Prob. 44ECh. 1.3 - Prob. 45ECh. 1.3 - Prob. 46ECh. 1.3 - Prob. 47ECh. 1.3 - Prob. 48ECh. 1.3 - Prob. 49ECh. 1.3 - Prob. 50ECh. 1.3 - Prob. 51ECh. 1.3 - Prob. 52ECh. 1.3 - Prob. 53ECh. 1.3 - Prob. 54ECh. 1.3 - Prob. 55ECh. 1.3 - Prob. 56ECh. 1.3 - Prob. 57ECh. 1.3 - Prob. 58ECh. 1.3 - Prob. 59ECh. 1.3 - Prob. 60ECh. 1.3 - Prob. 61ECh. 1.3 - Prob. 62ECh. 1.3 - Prob. 63ECh. 1.3 - Prob. 64ECh. 1.3 - Prob. 65ECh. 1.3 - Prob. 67ECh. 1.3 - Prob. 68ECh. 1.3 - Prob. 69ECh. 1.4 - Prob. 1QRCh. 1.4 - Prob. 2QRCh. 1.4 - Prob. 3QRCh. 1.4 - Prob. 4QRCh. 1.4 - Prob. 5QRCh. 1.4 - Prob. 6QRCh. 1.4 - Prob. 7QRCh. 1.4 - Prob. 8QRCh. 1.4 - Prob. 9QRCh. 1.4 - Prob. 10QRCh. 1.4 - In Exercises 14 find formulas for the functions...Ch. 1.4 - In Exercises 14 find formulas for the functions...Ch. 1.4 - Prob. 3ECh. 1.4 - Prob. 4ECh. 1.4 - Prob. 5ECh. 1.4 - Prob. 6ECh. 1.4 - Prob. 7ECh. 1.4 - Prob. 8ECh. 1.4 - Prob. 9ECh. 1.4 - Prob. 10ECh. 1.4 - Prob. 11ECh. 1.4 - Prob. 12ECh. 1.4 - Prob. 13ECh. 1.4 - Prob. 14ECh. 1.4 - Prob. 15ECh. 1.4 - Prob. 16ECh. 1.4 - Prob. 17ECh. 1.4 - Prob. 18ECh. 1.4 - Prob. 19ECh. 1.4 - Prob. 20ECh. 1.4 - Prob. 21ECh. 1.4 - Prob. 22ECh. 1.4 - Prob. 23ECh. 1.4 - Prob. 24ECh. 1.4 - Prob. 25ECh. 1.4 - Prob. 26ECh. 1.4 - Prob. 27ECh. 1.4 - Prob. 28ECh. 1.4 - Prob. 29ECh. 1.4 - Prob. 30ECh. 1.4 - Prob. 31ECh. 1.4 - Prob. 32ECh. 1.4 - Prob. 33ECh. 1.4 - Prob. 34ECh. 1.4 - Prob. 35ECh. 1.4 - Prob. 36ECh. 1.4 - Prob. 37ECh. 1.4 - Prob. 38ECh. 1.4 - Prob. 39ECh. 1.4 - Prob. 40ECh. 1.4 - Prob. 41ECh. 1.4 - Prob. 42ECh. 1.4 - Prob. 43ECh. 1.4 - Prob. 44ECh. 1.4 - Prob. 45ECh. 1.4 - Prob. 46ECh. 1.4 - Prob. 47ECh. 1.4 - Prob. 48ECh. 1.4 - Prob. 49ECh. 1.4 - Prob. 50ECh. 1.4 - Prob. 51ECh. 1.4 - Prob. 52ECh. 1.4 - Prob. 53ECh. 1.4 - Prob. 54ECh. 1.4 - Prob. 55ECh. 1.5 - Prob. 1QRCh. 1.5 - Prob. 2QRCh. 1.5 - Prob. 3QRCh. 1.5 - Prob. 4QRCh. 1.5 - Prob. 5QRCh. 1.5 - Prob. 6QRCh. 1.5 - Prob. 7QRCh. 1.5 - Prob. 8QRCh. 1.5 - Prob. 9QRCh. 1.5 - Prob. 10QRCh. 1.5 - Prob. 1ECh. 1.5 - Prob. 2ECh. 1.5 - Prob. 3ECh. 1.5 - Prob. 4ECh. 1.5 - Prob. 5ECh. 1.5 - Prob. 6ECh. 1.5 - Prob. 7ECh. 1.5 - Prob. 8ECh. 1.5 - Prob. 9ECh. 1.5 - Prob. 10ECh. 1.5 - Prob. 11ECh. 1.5 - Prob. 12ECh. 1.5 - Prob. 13ECh. 1.5 - In Exercises 1322, find a formula for f1x . Give...Ch. 1.5 - Prob. 15ECh. 1.5 - Prob. 16ECh. 1.5 - Prob. 17ECh. 1.5 - Prob. 18ECh. 1.5 - Prob. 19ECh. 1.5 - Prob. 20ECh. 1.5 - Prob. 21ECh. 1.5 - Prob. 22ECh. 1.5 - Prob. 23ECh. 1.5 - Prob. 24ECh. 1.5 - Prob. 25ECh. 1.5 - Prob. 26ECh. 1.5 - Prob. 27ECh. 1.5 - Prob. 28ECh. 1.5 - Prob. 29ECh. 1.5 - Prob. 30ECh. 1.5 - Prob. 31ECh. 1.5 - Prob. 32ECh. 1.5 - Prob. 33ECh. 1.5 - Prob. 34ECh. 1.5 - Prob. 35ECh. 1.5 - Prob. 36ECh. 1.5 - Prob. 37ECh. 1.5 - Prob. 38ECh. 1.5 - Prob. 39ECh. 1.5 - Prob. 40ECh. 1.5 - Prob. 41ECh. 1.5 - Prob. 42ECh. 1.5 - Prob. 43ECh. 1.5 - Prob. 44ECh. 1.5 - Prob. 45ECh. 1.5 - Prob. 46ECh. 1.5 - Prob. 47ECh. 1.5 - Prob. 48ECh. 1.5 - Prob. 49ECh. 1.5 - Prob. 50ECh. 1.5 - Prob. 51ECh. 1.6 - Prob. 1QRCh. 1.6 - Prob. 2QRCh. 1.6 - Prob. 3QRCh. 1.6 - Prob. 4QRCh. 1.6 - Prob. 5QRCh. 1.6 - Prob. 6QRCh. 1.6 - Prob. 7QRCh. 1.6 - Prob. 8QRCh. 1.6 - Prob. 9QRCh. 1.6 - Prob. 10QRCh. 1.6 - Prob. 1ECh. 1.6 - Prob. 2ECh. 1.6 - Prob. 3ECh. 1.6 - Prob. 4ECh. 1.6 - Prob. 5ECh. 1.6 - Prob. 6ECh. 1.6 - Prob. 7ECh. 1.6 - Prob. 8ECh. 1.6 - Prob. 9ECh. 1.6 - Prob. 10ECh. 1.6 - Prob. 11ECh. 1.6 - Prob. 12ECh. 1.6 - Prob. 13ECh. 1.6 - Prob. 14ECh. 1.6 - Prob. 15ECh. 1.6 - Prob. 16ECh. 1.6 - Prob. 17ECh. 1.6 - Prob. 18ECh. 1.6 - Prob. 19ECh. 1.6 - Prob. 20ECh. 1.6 - Prob. 21ECh. 1.6 - Prob. 22ECh. 1.6 - Prob. 23ECh. 1.6 - Prob. 24ECh. 1.6 - Prob. 25ECh. 1.6 - Prob. 26ECh. 1.6 - Prob. 27ECh. 1.6 - Prob. 28ECh. 1.6 - Prob. 29ECh. 1.6 - Prob. 30ECh. 1.6 - Prob. 31ECh. 1.6 - Prob. 32ECh. 1.6 - Prob. 33ECh. 1.6 - Prob. 34ECh. 1.6 - Prob. 35ECh. 1.6 - Prob. 36ECh. 1.6 - Prob. 37ECh. 1.6 - Prob. 38ECh. 1.6 - Prob. 39ECh. 1.6 - Prob. 40ECh. 1.6 - Prob. 41ECh. 1.6 - Prob. 42ECh. 1.6 - Prob. 43ECh. 1.6 - Prob. 44ECh. 1.6 - Prob. 45ECh. 1.6 - Prob. 46ECh. 1.6 - Prob. 47ECh. 1.6 - Prob. 48ECh. 1.6 - Prob. 49ECh. 1.6 - Prob. 50ECh. 1.6 - Prob. 51ECh. 1.6 - Prob. 52ECh. 1.6 - Prob. 53ECh. 1.6 - Prob. 54ECh. 1.6 - Prob. 55ECh. 1.6 - Prob. 56ECh. 1.6 - Prob. 57ECh. 1.6 - Prob. 58ECh. 1.6 - Prob. 59ECh. 1.6 - Prob. 60ECh. 1.6 - Prob. 61ECh. 1.6 - Prob. 62ECh. 1.6 - Prob. 63ECh. 1.6 - Prob. 64ECh. 1.6 - Prob. 65ECh. 1.6 - Prob. 66ECh. 1.6 - Prob. 67ECh. 1.6 - Prob. 68ECh. 1.7 - Prob. 1QRCh. 1.7 - Prob. 2QRCh. 1.7 - Prob. 3QRCh. 1.7 - Prob. 4QRCh. 1.7 - Prob. 5QRCh. 1.7 - Prob. 6QRCh. 1.7 - Prob. 7QRCh. 1.7 - Prob. 8QRCh. 1.7 - Prob. 9QRCh. 1.7 - Prob. 10QRCh. 1.7 - Prob. 1ECh. 1.7 - Prob. 2ECh. 1.7 - Prob. 3ECh. 1.7 - Prob. 4ECh. 1.7 - Prob. 5ECh. 1.7 - Prob. 6ECh. 1.7 - Prob. 7ECh. 1.7 - Prob. 8ECh. 1.7 - In Exercises 110, write a mathematical expression...Ch. 1.7 - Prob. 10ECh. 1.7 - Prob. 11ECh. 1.7 - Prob. 12ECh. 1.7 - Prob. 13ECh. 1.7 - In Exercises 1114, choose a variable and write a...Ch. 1.7 - Prob. 15ECh. 1.7 - In Exercises 1520, write the specified quantity as...Ch. 1.7 - Prob. 17ECh. 1.7 - Prob. 18ECh. 1.7 - Prob. 19ECh. 1.7 - Prob. 20ECh. 1.7 - Prob. 21ECh. 1.7 - Prob. 22ECh. 1.7 - Prob. 23ECh. 1.7 - Prob. 24ECh. 1.7 - Prob. 25ECh. 1.7 - Prob. 26ECh. 1.7 - Prob. 27ECh. 1.7 - Prob. 28ECh. 1.7 - Prob. 29ECh. 1.7 - Prob. 30ECh. 1.7 - Prob. 31ECh. 1.7 - Prob. 32ECh. 1.7 - Prob. 33ECh. 1.7 - Prob. 34ECh. 1.7 - Prob. 35ECh. 1.7 - In Exercises 2136, write an equation for the...Ch. 1.7 - Finding the Model and Solving Water is stored in a...Ch. 1.7 - Prob. 38ECh. 1.7 - Prob. 39ECh. 1.7 - Prob. 40ECh. 1.7 - Prob. 41ECh. 1.7 - Prob. 42ECh. 1.7 - Prob. 43ECh. 1.7 - Prob. 44ECh. 1.7 - Prob. 45ECh. 1.7 - Prob. 46ECh. 1.7 - Prob. 47ECh. 1.7 - Prob. 48ECh. 1.7 - Prob. 49ECh. 1.7 - Prob. 50ECh. 1.7 - Prob. 51ECh. 1 - Prob. 1RECh. 1 - Prob. 2RECh. 1 - Prob. 3RECh. 1 - Prob. 4RECh. 1 - Prob. 5RECh. 1 - Prob. 6RECh. 1 - Prob. 7RECh. 1 - Prob. 8RECh. 1 - Prob. 9RECh. 1 - Prob. 10RECh. 1 - Prob. 11RECh. 1 - Prob. 12RECh. 1 - Prob. 13RECh. 1 - Prob. 14RECh. 1 - Prob. 15RECh. 1 - Prob. 16RECh. 1 - Prob. 17RECh. 1 - Prob. 18RECh. 1 - Prob. 19RECh. 1 - Prob. 20RECh. 1 - Prob. 21RECh. 1 - Prob. 22RECh. 1 - Prob. 23RECh. 1 - Prob. 24RECh. 1 - Prob. 25RECh. 1 - Prob. 26RECh. 1 - Prob. 27RECh. 1 - Prob. 28RECh. 1 - Prob. 29RECh. 1 - Prob. 30RECh. 1 - Prob. 31RECh. 1 - Prob. 32RECh. 1 - Prob. 33RECh. 1 - Prob. 34RECh. 1 - Prob. 35RECh. 1 - Prob. 36RECh. 1 - Prob. 37RECh. 1 - Prob. 38RECh. 1 - Prob. 39RECh. 1 - Prob. 40RECh. 1 - Prob. 41RECh. 1 - Prob. 42RECh. 1 - Prob. 43RECh. 1 - Prob. 44RECh. 1 - Prob. 45RECh. 1 - Prob. 46RECh. 1 - Prob. 47RECh. 1 - Prob. 48RECh. 1 - Prob. 49RECh. 1 - Prob. 50RECh. 1 - Prob. 51RECh. 1 - Prob. 52RECh. 1 - Prob. 53RECh. 1 - Prob. 54RECh. 1 - Prob. 55RECh. 1 - Prob. 56RECh. 1 - Prob. 57RECh. 1 - Prob. 58RECh. 1 - Prob. 59RECh. 1 - Prob. 60RECh. 1 - In Exercises 5964, write the specified quantity as...Ch. 1 - Prob. 62RECh. 1 - Prob. 63RECh. 1 - Prob. 64RECh. 1 - Prob. 65RECh. 1 - Prob. 67RECh. 1 - Prob. 68RE
Knowledge Booster
Background pattern image
Calculus
Learn more about
Need a deep-dive on the concept behind this application? Look no further. Learn more about this topic, calculus and related others by exploring similar questions and additional content below.
Similar questions
SEE MORE QUESTIONS
Recommended textbooks for you
Text book image
Calculus: Early Transcendentals
Calculus
ISBN:9781285741550
Author:James Stewart
Publisher:Cengage Learning
Text book image
Thomas' Calculus (14th Edition)
Calculus
ISBN:9780134438986
Author:Joel R. Hass, Christopher E. Heil, Maurice D. Weir
Publisher:PEARSON
Text book image
Calculus: Early Transcendentals (3rd Edition)
Calculus
ISBN:9780134763644
Author:William L. Briggs, Lyle Cochran, Bernard Gillett, Eric Schulz
Publisher:PEARSON
Text book image
Calculus: Early Transcendentals
Calculus
ISBN:9781319050740
Author:Jon Rogawski, Colin Adams, Robert Franzosa
Publisher:W. H. Freeman
Text book image
Precalculus
Calculus
ISBN:9780135189405
Author:Michael Sullivan
Publisher:PEARSON
Text book image
Calculus: Early Transcendental Functions
Calculus
ISBN:9781337552516
Author:Ron Larson, Bruce H. Edwards
Publisher:Cengage Learning
SEE MORE TEXTBOOKS
What is a Linear Equation in One Variable?; Author: Don't Memorise;https://www.youtube.com/watch?v=lDOYdBgtnjY;License: Standard YouTube License, CC-BY
Linear Equation | Solving Linear Equations | What is Linear Equation in one variable ?; Author: Najam Academy;https://www.youtube.com/watch?v=tHm3X_Ta_iE;License: Standard YouTube License, CC-BY