
a.
To determine which of the twelve basic functions are inverses of each other.
The exponential function and the logarithmic function are the basic functions which are inverses of each other.
Concept Used:
The twelve basic functions:
1)
2)
3)
4)
5)
6)
7)
8)
9)
10)
11)
12)
Calculation:
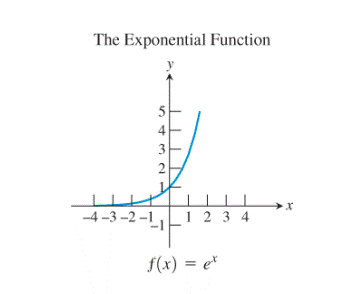
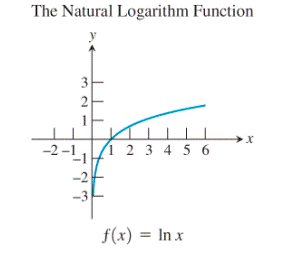
Observe the natural logarithm function and the exponential function:
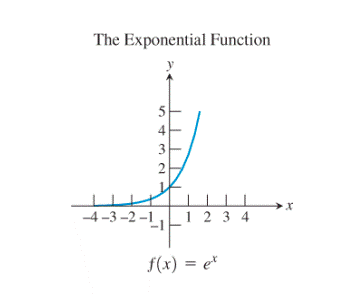
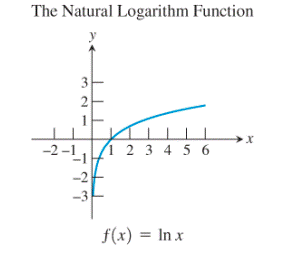
The graph of the exponential function seems to be the reflection of the logarithmic function about
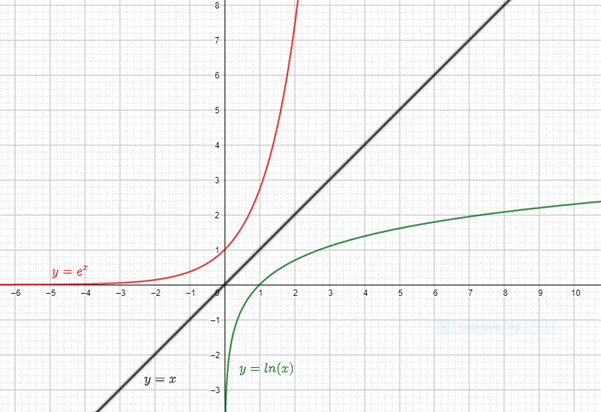
Thus, the exponential function and the logarithmic function are the basic functions which are inverses of each other. Also, no any other pair of functions seems to be showing this kind of relationship.
Conclusion:
The exponential function and the logarithmic function are the basic functions which are inverses of each other.
b.
To determine which among the basic functions are inverses of their own.
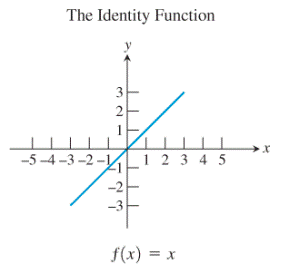
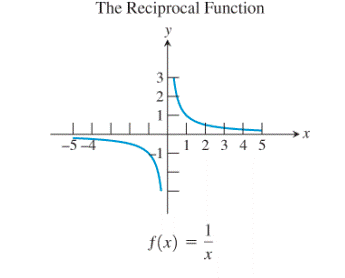
The identity function and the reciprocal function are the basic functions which are the inverses of their own.
Calculation:
Consider the identity function along with its graph:
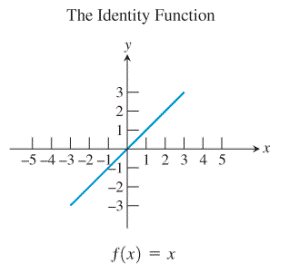
The graph is that of the line
Then, reflecting the graph of the identity function about the line
Thus, the identity function is the inverse of itself.
Now, consider the reciprocal function:
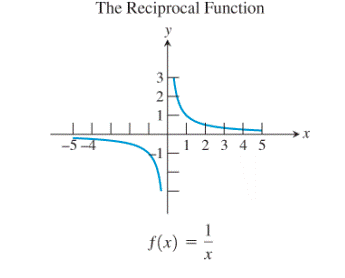
The graph of the function remains unchanged even after reflecting it about the line
Thus, the reciprocal function is also the inverse of itself.
No any other functions seem to show this property.
Thus, the identity function and the reciprocal function are the basic functions which are inverses of their own.
Conclusion:
The identity function and the reciprocal function are the basic functions which are the inverses of their own.
c.
To determine the basic function which is the inverse of another basic function when its domain is restricted to
Calculation:
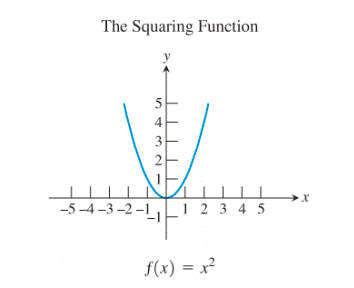
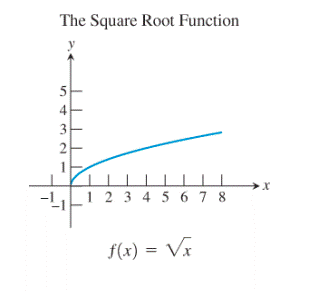
Consider the squaring function:
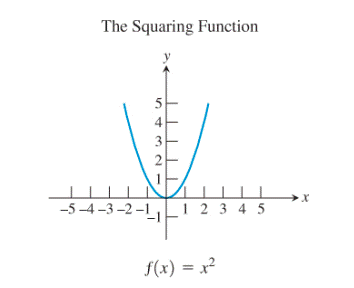
Restrict the domain of the squaring function to
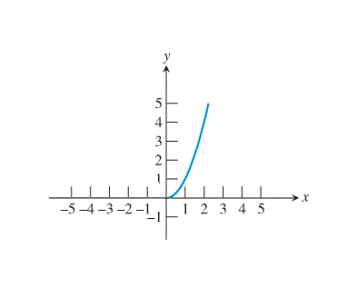
Now, reflect the graph so obtained about the line
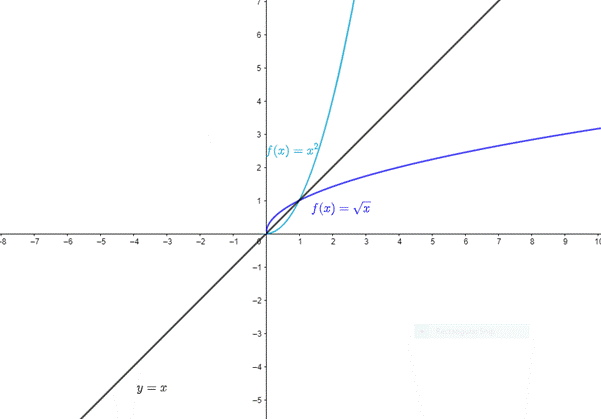
Thus, the restricted squaring function gives the square root function when it is reflected about the line
Thus, the basic function which gives the inverse of another basic function when its domain is restricted to
Conclusion:
The basic function which gives the inverse of another basic function when its domain is restricted to
Chapter 1 Solutions
PRECALCULUS:...COMMON CORE ED.-W/ACCESS
- Calculus lll May I please have the statements with blank lines completed; furthermore, may I please have the text box completed? Thank youarrow_forwardCalculus lll May I please have the statements completed for the following text lines and box? Thank you so much,arrow_forwardCalculus lll May I please have the solution for the following exercise? Thank you so mucharrow_forward
- Calculus lll May I please have the statement completed for the following box? Thank you so much,arrow_forwardCalculus lll May I please have the solution for the following exercise? Thank you so mucharrow_forwardUse a graphing calculator to find where the curves intersect and to find the area between the curves. y=ex, y=-x²-4x a. The left point of intersection is (Type integers or decimals rounded to the nearest thousandth as needed. Type an ordered pair.)arrow_forward
- Find the area between the curves. x= -5, x=3, y=2x² +9, y=0 The area between the curves is (Round to the nearest whole number as needed.)arrow_forwardcan you solve these questions with step by step with clear explaination pleasearrow_forwardFind the area between the following curves. x=-1, x=3, y=x-1, and y=0 The area between the curves is (Simplify your answer.)arrow_forward
 Calculus: Early TranscendentalsCalculusISBN:9781285741550Author:James StewartPublisher:Cengage Learning
Calculus: Early TranscendentalsCalculusISBN:9781285741550Author:James StewartPublisher:Cengage Learning Thomas' Calculus (14th Edition)CalculusISBN:9780134438986Author:Joel R. Hass, Christopher E. Heil, Maurice D. WeirPublisher:PEARSON
Thomas' Calculus (14th Edition)CalculusISBN:9780134438986Author:Joel R. Hass, Christopher E. Heil, Maurice D. WeirPublisher:PEARSON Calculus: Early Transcendentals (3rd Edition)CalculusISBN:9780134763644Author:William L. Briggs, Lyle Cochran, Bernard Gillett, Eric SchulzPublisher:PEARSON
Calculus: Early Transcendentals (3rd Edition)CalculusISBN:9780134763644Author:William L. Briggs, Lyle Cochran, Bernard Gillett, Eric SchulzPublisher:PEARSON Calculus: Early TranscendentalsCalculusISBN:9781319050740Author:Jon Rogawski, Colin Adams, Robert FranzosaPublisher:W. H. Freeman
Calculus: Early TranscendentalsCalculusISBN:9781319050740Author:Jon Rogawski, Colin Adams, Robert FranzosaPublisher:W. H. Freeman
 Calculus: Early Transcendental FunctionsCalculusISBN:9781337552516Author:Ron Larson, Bruce H. EdwardsPublisher:Cengage Learning
Calculus: Early Transcendental FunctionsCalculusISBN:9781337552516Author:Ron Larson, Bruce H. EdwardsPublisher:Cengage Learning





