PRECALCULUS:...COMMON CORE ED.-W/ACCESS
10th Edition
ISBN: 9780134781839
Author: Demana
Publisher: PEARSON
expand_more
expand_more
format_list_bulleted
Videos
Expert Solution & Answer
Chapter 1.5, Problem 10E
Solution
a.
To check: The graph of the relation is a function
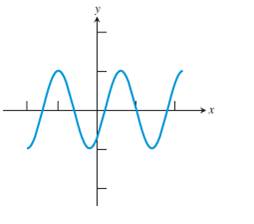
Given information:
The graph is given below:
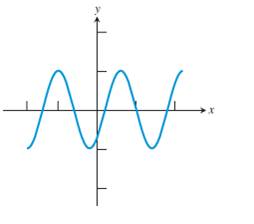
Concept used:
Vertical line test :The test state that a graph represent a function if and only if all vertical lines intersect the graph at most once.
Explanation:
Here from the graph can understand that when doing the vertical line test ,the vertical line intersect at only one point .So the graph pass in the vertical line test .
Hence the given graph of a relation is afunction.
b.
To check: The relation that have an inverse and is a function .
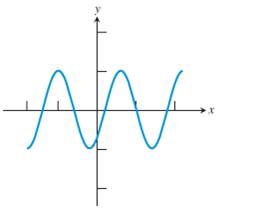
Given information:
The graph is given below.
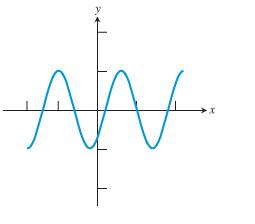
Concept used:
The ordered pair
The inverse of a relation is a function if and only if each horizontal line intersects the graph
of the original relation in at most one point.
Explanations:
Here for each ordered pair
But when do the horizontal line test it intersects more than point so it did not the horizontal line test.
Hence this inverse of this relation is not a function.
Chapter 1 Solutions
PRECALCULUS:...COMMON CORE ED.-W/ACCESS
Ch. 1.1 - Prob. 1QRCh. 1.1 - Prob. 2QRCh. 1.1 - Prob. 3QRCh. 1.1 - Prob. 4QRCh. 1.1 - Prob. 5QRCh. 1.1 - Prob. 6QRCh. 1.1 - Prob. 7QRCh. 1.1 - Prob. 8QRCh. 1.1 - Prob. 9QRCh. 1.1 - Prob. 10QR
Ch. 1.1 - Prob. 1ECh. 1.1 - Prob. 2ECh. 1.1 - Prob. 3ECh. 1.1 - Prob. 4ECh. 1.1 - Prob. 5ECh. 1.1 - Prob. 6ECh. 1.1 - Prob. 7ECh. 1.1 - Prob. 8ECh. 1.1 - Prob. 9ECh. 1.1 - Prob. 10ECh. 1.1 - Prob. 11ECh. 1.1 - Prob. 12ECh. 1.1 - Prob. 13ECh. 1.1 - Prob. 14ECh. 1.1 - Prob. 15ECh. 1.1 - Prob. 16ECh. 1.1 - Prob. 18ECh. 1.1 - Prob. 19ECh. 1.1 - Prob. 20ECh. 1.1 - Prob. 21ECh. 1.1 - Prob. 22ECh. 1.1 - Prob. 23ECh. 1.1 - Prob. 24ECh. 1.1 - Prob. 25ECh. 1.1 - Prob. 26ECh. 1.1 - Prob. 27ECh. 1.1 - Prob. 28ECh. 1.1 - Prob. 29ECh. 1.1 - Prob. 30ECh. 1.1 - Prob. 31ECh. 1.1 - Prob. 32ECh. 1.1 - Prob. 33ECh. 1.1 - Prob. 34ECh. 1.1 - Prob. 35ECh. 1.1 - Prob. 36ECh. 1.1 - Prob. 37ECh. 1.1 - Prob. 38ECh. 1.1 - Prob. 39ECh. 1.1 - Prob. 40ECh. 1.1 - Prob. 41ECh. 1.1 - Prob. 42ECh. 1.1 - Prob. 43ECh. 1.1 - Prob. 44ECh. 1.1 - Prob. 45ECh. 1.1 - Prob. 46ECh. 1.1 - Prob. 47ECh. 1.1 - Prob. 48ECh. 1.1 - Prob. 49ECh. 1.1 - Prob. 50ECh. 1.1 - Prob. 51ECh. 1.1 - Prob. 52ECh. 1.1 - Prob. 53ECh. 1.1 - Prob. 54ECh. 1.1 - Prob. 55ECh. 1.1 - Prob. 56ECh. 1.1 - Prob. 57ECh. 1.1 - Prob. 58ECh. 1.1 - Prob. 59ECh. 1.1 - Prob. 60ECh. 1.1 - Prob. 61ECh. 1.1 - Prob. 62ECh. 1.1 - Prob. 63ECh. 1.2 - Prob. 1QRCh. 1.2 - Prob. 2QRCh. 1.2 - Prob. 3QRCh. 1.2 - Prob. 4QRCh. 1.2 - Prob. 5QRCh. 1.2 - Prob. 6QRCh. 1.2 - Prob. 7QRCh. 1.2 - Prob. 8QRCh. 1.2 - Prob. 9QRCh. 1.2 - Prob. 10QRCh. 1.2 - Prob. 1ECh. 1.2 - Prob. 2ECh. 1.2 - Prob. 3ECh. 1.2 - Prob. 4ECh. 1.2 - Prob. 5ECh. 1.2 - Prob. 6ECh. 1.2 - Prob. 7ECh. 1.2 - Prob. 8ECh. 1.2 - Prob. 9ECh. 1.2 - Prob. 10ECh. 1.2 - Prob. 11ECh. 1.2 - Prob. 12ECh. 1.2 - Prob. 13ECh. 1.2 - Prob. 14ECh. 1.2 - Prob. 15ECh. 1.2 - Prob. 16ECh. 1.2 - Prob. 17ECh. 1.2 - Prob. 18ECh. 1.2 - Prob. 19ECh. 1.2 - Prob. 20ECh. 1.2 - Prob. 21ECh. 1.2 - Prob. 22ECh. 1.2 - Prob. 23ECh. 1.2 - Prob. 24ECh. 1.2 - Prob. 25ECh. 1.2 - Prob. 26ECh. 1.2 - Prob. 27ECh. 1.2 - Prob. 28ECh. 1.2 - Prob. 29ECh. 1.2 - Prob. 30ECh. 1.2 - Prob. 31ECh. 1.2 - Prob. 32ECh. 1.2 - Prob. 33ECh. 1.2 - Prob. 34ECh. 1.2 - Prob. 35ECh. 1.2 - Prob. 36ECh. 1.2 - Prob. 37ECh. 1.2 - Prob. 38ECh. 1.2 - Prob. 39ECh. 1.2 - Prob. 40ECh. 1.2 - Prob. 41ECh. 1.2 - Prob. 42ECh. 1.2 - Prob. 43ECh. 1.2 - Prob. 44ECh. 1.2 - Prob. 45ECh. 1.2 - Prob. 46ECh. 1.2 - Prob. 47ECh. 1.2 - Prob. 48ECh. 1.2 - Prob. 49ECh. 1.2 - Prob. 50ECh. 1.2 - Prob. 51ECh. 1.2 - Prob. 52ECh. 1.2 - Prob. 53ECh. 1.2 - Prob. 54ECh. 1.2 - Prob. 55ECh. 1.2 - Prob. 56ECh. 1.2 - Prob. 57ECh. 1.2 - Prob. 58ECh. 1.2 - Prob. 59ECh. 1.2 - Prob. 60ECh. 1.2 - Prob. 61ECh. 1.2 - Prob. 62ECh. 1.2 - Prob. 63ECh. 1.2 - Prob. 64ECh. 1.2 - Prob. 65ECh. 1.2 - Prob. 66ECh. 1.2 - Prob. 67ECh. 1.2 - Prob. 68ECh. 1.2 - Prob. 69ECh. 1.2 - Prob. 70ECh. 1.2 - Prob. 71ECh. 1.2 - Prob. 72ECh. 1.2 - Prob. 73ECh. 1.2 - Prob. 74ECh. 1.2 - Prob. 75ECh. 1.2 - Prob. 76ECh. 1.2 - Prob. 77ECh. 1.2 - Prob. 78ECh. 1.2 - Prob. 79ECh. 1.2 - Prob. 80ECh. 1.2 - Prob. 81ECh. 1.2 - Prob. 82ECh. 1.2 - Prob. 83ECh. 1.2 - Prob. 84ECh. 1.2 - Prob. 85ECh. 1.2 - Prob. 86ECh. 1.2 - Prob. 87ECh. 1.3 - Prob. 1QRCh. 1.3 - In Exercises 110, evaluate the expression without...Ch. 1.3 - In Exercises 110, evaluate the expression without...Ch. 1.3 - Prob. 4QRCh. 1.3 - In Exercises 110, evaluate the expression without...Ch. 1.3 - Prob. 6QRCh. 1.3 - Prob. 7QRCh. 1.3 - Prob. 8QRCh. 1.3 - Prob. 9QRCh. 1.3 - Prob. 10QRCh. 1.3 - Prob. 1ECh. 1.3 - Prob. 2ECh. 1.3 - In Exercises 112, each graph is a slight variation...Ch. 1.3 - Prob. 4ECh. 1.3 - Prob. 5ECh. 1.3 - Prob. 6ECh. 1.3 - Prob. 7ECh. 1.3 - Prob. 8ECh. 1.3 - Prob. 9ECh. 1.3 - Prob. 10ECh. 1.3 - Prob. 11ECh. 1.3 - Prob. 12ECh. 1.3 - Prob. 13ECh. 1.3 - Prob. 14ECh. 1.3 - Prob. 15ECh. 1.3 - Prob. 16ECh. 1.3 - Prob. 17ECh. 1.3 - Prob. 18ECh. 1.3 - Prob. 19ECh. 1.3 - Prob. 20ECh. 1.3 - Prob. 21ECh. 1.3 - Prob. 22ECh. 1.3 - Prob. 23ECh. 1.3 - Prob. 24ECh. 1.3 - Prob. 25ECh. 1.3 - Prob. 26ECh. 1.3 - Prob. 27ECh. 1.3 - Prob. 28ECh. 1.3 - Prob. 29ECh. 1.3 - Prob. 30ECh. 1.3 - Prob. 31ECh. 1.3 - Prob. 32ECh. 1.3 - Prob. 33ECh. 1.3 - Prob. 34ECh. 1.3 - Prob. 35ECh. 1.3 - Prob. 36ECh. 1.3 - Prob. 37ECh. 1.3 - Prob. 38ECh. 1.3 - Prob. 39ECh. 1.3 - Prob. 40ECh. 1.3 - Prob. 41ECh. 1.3 - Prob. 42ECh. 1.3 - Prob. 43ECh. 1.3 - Prob. 44ECh. 1.3 - Prob. 45ECh. 1.3 - Prob. 46ECh. 1.3 - Prob. 47ECh. 1.3 - Prob. 48ECh. 1.3 - Prob. 49ECh. 1.3 - Prob. 50ECh. 1.3 - Prob. 51ECh. 1.3 - Prob. 52ECh. 1.3 - Prob. 53ECh. 1.3 - Prob. 54ECh. 1.3 - Prob. 55ECh. 1.3 - Prob. 56ECh. 1.3 - Prob. 57ECh. 1.3 - Prob. 58ECh. 1.3 - Prob. 59ECh. 1.3 - Prob. 60ECh. 1.3 - Prob. 61ECh. 1.3 - Prob. 62ECh. 1.3 - Prob. 63ECh. 1.3 - Prob. 64ECh. 1.3 - Prob. 65ECh. 1.3 - Prob. 67ECh. 1.3 - Prob. 68ECh. 1.3 - Prob. 69ECh. 1.4 - Prob. 1QRCh. 1.4 - Prob. 2QRCh. 1.4 - Prob. 3QRCh. 1.4 - Prob. 4QRCh. 1.4 - Prob. 5QRCh. 1.4 - Prob. 6QRCh. 1.4 - Prob. 7QRCh. 1.4 - Prob. 8QRCh. 1.4 - Prob. 9QRCh. 1.4 - Prob. 10QRCh. 1.4 - In Exercises 14 find formulas for the functions...Ch. 1.4 - In Exercises 14 find formulas for the functions...Ch. 1.4 - Prob. 3ECh. 1.4 - Prob. 4ECh. 1.4 - Prob. 5ECh. 1.4 - Prob. 6ECh. 1.4 - Prob. 7ECh. 1.4 - Prob. 8ECh. 1.4 - Prob. 9ECh. 1.4 - Prob. 10ECh. 1.4 - Prob. 11ECh. 1.4 - Prob. 12ECh. 1.4 - Prob. 13ECh. 1.4 - Prob. 14ECh. 1.4 - Prob. 15ECh. 1.4 - Prob. 16ECh. 1.4 - Prob. 17ECh. 1.4 - Prob. 18ECh. 1.4 - Prob. 19ECh. 1.4 - Prob. 20ECh. 1.4 - Prob. 21ECh. 1.4 - Prob. 22ECh. 1.4 - Prob. 23ECh. 1.4 - Prob. 24ECh. 1.4 - Prob. 25ECh. 1.4 - Prob. 26ECh. 1.4 - Prob. 27ECh. 1.4 - Prob. 28ECh. 1.4 - Prob. 29ECh. 1.4 - Prob. 30ECh. 1.4 - Prob. 31ECh. 1.4 - Prob. 32ECh. 1.4 - Prob. 33ECh. 1.4 - Prob. 34ECh. 1.4 - Prob. 35ECh. 1.4 - Prob. 36ECh. 1.4 - Prob. 37ECh. 1.4 - Prob. 38ECh. 1.4 - Prob. 39ECh. 1.4 - Prob. 40ECh. 1.4 - Prob. 41ECh. 1.4 - Prob. 42ECh. 1.4 - Prob. 43ECh. 1.4 - Prob. 44ECh. 1.4 - Prob. 45ECh. 1.4 - Prob. 46ECh. 1.4 - Prob. 47ECh. 1.4 - Prob. 48ECh. 1.4 - Prob. 49ECh. 1.4 - Prob. 50ECh. 1.4 - Prob. 51ECh. 1.4 - Prob. 52ECh. 1.4 - Prob. 53ECh. 1.4 - Prob. 54ECh. 1.4 - Prob. 55ECh. 1.5 - Prob. 1QRCh. 1.5 - Prob. 2QRCh. 1.5 - Prob. 3QRCh. 1.5 - Prob. 4QRCh. 1.5 - Prob. 5QRCh. 1.5 - Prob. 6QRCh. 1.5 - Prob. 7QRCh. 1.5 - Prob. 8QRCh. 1.5 - Prob. 9QRCh. 1.5 - Prob. 10QRCh. 1.5 - Prob. 1ECh. 1.5 - Prob. 2ECh. 1.5 - Prob. 3ECh. 1.5 - Prob. 4ECh. 1.5 - Prob. 5ECh. 1.5 - Prob. 6ECh. 1.5 - Prob. 7ECh. 1.5 - Prob. 8ECh. 1.5 - Prob. 9ECh. 1.5 - Prob. 10ECh. 1.5 - Prob. 11ECh. 1.5 - Prob. 12ECh. 1.5 - Prob. 13ECh. 1.5 - In Exercises 1322, find a formula for f1x . Give...Ch. 1.5 - Prob. 15ECh. 1.5 - Prob. 16ECh. 1.5 - Prob. 17ECh. 1.5 - Prob. 18ECh. 1.5 - Prob. 19ECh. 1.5 - Prob. 20ECh. 1.5 - Prob. 21ECh. 1.5 - Prob. 22ECh. 1.5 - Prob. 23ECh. 1.5 - Prob. 24ECh. 1.5 - Prob. 25ECh. 1.5 - Prob. 26ECh. 1.5 - Prob. 27ECh. 1.5 - Prob. 28ECh. 1.5 - Prob. 29ECh. 1.5 - Prob. 30ECh. 1.5 - Prob. 31ECh. 1.5 - Prob. 32ECh. 1.5 - Prob. 33ECh. 1.5 - Prob. 34ECh. 1.5 - Prob. 35ECh. 1.5 - Prob. 36ECh. 1.5 - Prob. 37ECh. 1.5 - Prob. 38ECh. 1.5 - Prob. 39ECh. 1.5 - Prob. 40ECh. 1.5 - Prob. 41ECh. 1.5 - Prob. 42ECh. 1.5 - Prob. 43ECh. 1.5 - Prob. 44ECh. 1.5 - Prob. 45ECh. 1.5 - Prob. 46ECh. 1.5 - Prob. 47ECh. 1.5 - Prob. 48ECh. 1.5 - Prob. 49ECh. 1.5 - Prob. 50ECh. 1.5 - Prob. 51ECh. 1.6 - Prob. 1QRCh. 1.6 - Prob. 2QRCh. 1.6 - Prob. 3QRCh. 1.6 - Prob. 4QRCh. 1.6 - Prob. 5QRCh. 1.6 - Prob. 6QRCh. 1.6 - Prob. 7QRCh. 1.6 - Prob. 8QRCh. 1.6 - Prob. 9QRCh. 1.6 - Prob. 10QRCh. 1.6 - Prob. 1ECh. 1.6 - Prob. 2ECh. 1.6 - Prob. 3ECh. 1.6 - Prob. 4ECh. 1.6 - Prob. 5ECh. 1.6 - Prob. 6ECh. 1.6 - Prob. 7ECh. 1.6 - Prob. 8ECh. 1.6 - Prob. 9ECh. 1.6 - Prob. 10ECh. 1.6 - Prob. 11ECh. 1.6 - Prob. 12ECh. 1.6 - Prob. 13ECh. 1.6 - Prob. 14ECh. 1.6 - Prob. 15ECh. 1.6 - Prob. 16ECh. 1.6 - Prob. 17ECh. 1.6 - Prob. 18ECh. 1.6 - Prob. 19ECh. 1.6 - Prob. 20ECh. 1.6 - Prob. 21ECh. 1.6 - Prob. 22ECh. 1.6 - Prob. 23ECh. 1.6 - Prob. 24ECh. 1.6 - Prob. 25ECh. 1.6 - Prob. 26ECh. 1.6 - Prob. 27ECh. 1.6 - Prob. 28ECh. 1.6 - Prob. 29ECh. 1.6 - Prob. 30ECh. 1.6 - Prob. 31ECh. 1.6 - Prob. 32ECh. 1.6 - Prob. 33ECh. 1.6 - Prob. 34ECh. 1.6 - Prob. 35ECh. 1.6 - Prob. 36ECh. 1.6 - Prob. 37ECh. 1.6 - Prob. 38ECh. 1.6 - Prob. 39ECh. 1.6 - Prob. 40ECh. 1.6 - Prob. 41ECh. 1.6 - Prob. 42ECh. 1.6 - Prob. 43ECh. 1.6 - Prob. 44ECh. 1.6 - Prob. 45ECh. 1.6 - Prob. 46ECh. 1.6 - Prob. 47ECh. 1.6 - Prob. 48ECh. 1.6 - Prob. 49ECh. 1.6 - Prob. 50ECh. 1.6 - Prob. 51ECh. 1.6 - Prob. 52ECh. 1.6 - Prob. 53ECh. 1.6 - Prob. 54ECh. 1.6 - Prob. 55ECh. 1.6 - Prob. 56ECh. 1.6 - Prob. 57ECh. 1.6 - Prob. 58ECh. 1.6 - Prob. 59ECh. 1.6 - Prob. 60ECh. 1.6 - Prob. 61ECh. 1.6 - Prob. 62ECh. 1.6 - Prob. 63ECh. 1.6 - Prob. 64ECh. 1.6 - Prob. 65ECh. 1.6 - Prob. 66ECh. 1.6 - Prob. 67ECh. 1.6 - Prob. 68ECh. 1.7 - Prob. 1QRCh. 1.7 - Prob. 2QRCh. 1.7 - Prob. 3QRCh. 1.7 - Prob. 4QRCh. 1.7 - Prob. 5QRCh. 1.7 - Prob. 6QRCh. 1.7 - Prob. 7QRCh. 1.7 - Prob. 8QRCh. 1.7 - Prob. 9QRCh. 1.7 - Prob. 10QRCh. 1.7 - Prob. 1ECh. 1.7 - Prob. 2ECh. 1.7 - Prob. 3ECh. 1.7 - Prob. 4ECh. 1.7 - Prob. 5ECh. 1.7 - Prob. 6ECh. 1.7 - Prob. 7ECh. 1.7 - Prob. 8ECh. 1.7 - In Exercises 110, write a mathematical expression...Ch. 1.7 - Prob. 10ECh. 1.7 - Prob. 11ECh. 1.7 - Prob. 12ECh. 1.7 - Prob. 13ECh. 1.7 - In Exercises 1114, choose a variable and write a...Ch. 1.7 - Prob. 15ECh. 1.7 - In Exercises 1520, write the specified quantity as...Ch. 1.7 - Prob. 17ECh. 1.7 - Prob. 18ECh. 1.7 - Prob. 19ECh. 1.7 - Prob. 20ECh. 1.7 - Prob. 21ECh. 1.7 - Prob. 22ECh. 1.7 - Prob. 23ECh. 1.7 - Prob. 24ECh. 1.7 - Prob. 25ECh. 1.7 - Prob. 26ECh. 1.7 - Prob. 27ECh. 1.7 - Prob. 28ECh. 1.7 - Prob. 29ECh. 1.7 - Prob. 30ECh. 1.7 - Prob. 31ECh. 1.7 - Prob. 32ECh. 1.7 - Prob. 33ECh. 1.7 - Prob. 34ECh. 1.7 - Prob. 35ECh. 1.7 - In Exercises 2136, write an equation for the...Ch. 1.7 - Finding the Model and Solving Water is stored in a...Ch. 1.7 - Prob. 38ECh. 1.7 - Prob. 39ECh. 1.7 - Prob. 40ECh. 1.7 - Prob. 41ECh. 1.7 - Prob. 42ECh. 1.7 - Prob. 43ECh. 1.7 - Prob. 44ECh. 1.7 - Prob. 45ECh. 1.7 - Prob. 46ECh. 1.7 - Prob. 47ECh. 1.7 - Prob. 48ECh. 1.7 - Prob. 49ECh. 1.7 - Prob. 50ECh. 1.7 - Prob. 51ECh. 1 - Prob. 1RECh. 1 - Prob. 2RECh. 1 - Prob. 3RECh. 1 - Prob. 4RECh. 1 - Prob. 5RECh. 1 - Prob. 6RECh. 1 - Prob. 7RECh. 1 - Prob. 8RECh. 1 - Prob. 9RECh. 1 - Prob. 10RECh. 1 - Prob. 11RECh. 1 - Prob. 12RECh. 1 - Prob. 13RECh. 1 - Prob. 14RECh. 1 - Prob. 15RECh. 1 - Prob. 16RECh. 1 - Prob. 17RECh. 1 - Prob. 18RECh. 1 - Prob. 19RECh. 1 - Prob. 20RECh. 1 - Prob. 21RECh. 1 - Prob. 22RECh. 1 - Prob. 23RECh. 1 - Prob. 24RECh. 1 - Prob. 25RECh. 1 - Prob. 26RECh. 1 - Prob. 27RECh. 1 - Prob. 28RECh. 1 - Prob. 29RECh. 1 - Prob. 30RECh. 1 - Prob. 31RECh. 1 - Prob. 32RECh. 1 - Prob. 33RECh. 1 - Prob. 34RECh. 1 - Prob. 35RECh. 1 - Prob. 36RECh. 1 - Prob. 37RECh. 1 - Prob. 38RECh. 1 - Prob. 39RECh. 1 - Prob. 40RECh. 1 - Prob. 41RECh. 1 - Prob. 42RECh. 1 - Prob. 43RECh. 1 - Prob. 44RECh. 1 - Prob. 45RECh. 1 - Prob. 46RECh. 1 - Prob. 47RECh. 1 - Prob. 48RECh. 1 - Prob. 49RECh. 1 - Prob. 50RECh. 1 - Prob. 51RECh. 1 - Prob. 52RECh. 1 - Prob. 53RECh. 1 - Prob. 54RECh. 1 - Prob. 55RECh. 1 - Prob. 56RECh. 1 - Prob. 57RECh. 1 - Prob. 58RECh. 1 - Prob. 59RECh. 1 - Prob. 60RECh. 1 - In Exercises 5964, write the specified quantity as...Ch. 1 - Prob. 62RECh. 1 - Prob. 63RECh. 1 - Prob. 64RECh. 1 - Prob. 65RECh. 1 - Prob. 67RECh. 1 - Prob. 68RE
Knowledge Booster
Learn more about
Need a deep-dive on the concept behind this application? Look no further. Learn more about this topic, calculus and related others by exploring similar questions and additional content below.Similar questions
- Calculate the max value of the directional derivatearrow_forwardCalculus III May I please have the example, definition semicolons, and all blanks completed and solved? Thank you so much,arrow_forwardA company estimates that the revenue (in dollars) from the sale of x doghouses is given by R(x) = 12,000 In (0.02x+1). Use the differential to approximate the change in revenue from the sale of one more doghouse if 80 doghouses have already been sold. The revenue will increase by $ if one more doghouse is made. (Round to the nearest cent as needed.)arrow_forward
- The population of bacteria (in millions) in a certain culture x hours after an experimental 20x nutrient is introduced into the culture is P(x) = - 2 Use the differential to approximate the changes in population for the following changes in x. 8+x a. 1 to 1.5 b. 3 to 3.25 a. Use the differential to approximate the change in population for x=1 to 1.5. Between 1 and 1.5 hours, the population of bacteria changes by million. (Round to three decimal places as needed.)arrow_forwardThe demand for grass seed (in thousands of pounds) at price p dollars is given by the following function. D(p) 3p³-2p² + 1460 Use the differential to approximate the changes in demand for the following changes in p. a. $4 to $4.11 b. $6 to $6.19arrow_forwardLet the region R be the area enclosed by the function f(x) = 3 ln (x) and g(x) = 3 x + 1. Write an integral in terms of x and also an integral in terms of y that would represent the area of the region R. If necessary, round limit values to the nearest thousandth. Answer Attempt 1 out of 2 y 7 10 6 5 4 3 2 -1 2 3 4 5 6 x2 dx x1 = x2 = x1 Y1 = Y2 = Y1 dyarrow_forward
- A manufacturer of handcrafted wine racks has determined that the cost to produce x units per month is given by C = 0.3x² + 7,000. How fast is the cost per month changing when production is changing at the rate of 14 units per month and the production level is 80 units? Costs are increasing at the rate of $ (Round to the nearest dollar as needed.) per month at this production level.arrow_forwarddy Assume x and y are functions of t. Evaluate for 2xy -3x+2y³ = - 72, with the conditions dt dx dt = -8, x=2, y = -3. dy dt (Type an exact answer in simplified form.)arrow_forwardConsider the sequence below: 1 1 1 (a) Express this sequence as a recurrence relation (b) Express this sequence in the form {a}=1 (c) Does this sequence converge or diverge? Justify your answer. Consider the sequence below: 1 1 1 1, 4' 9' 16' (a) Express this sequence in the form {ak}=1 (b) Does this sequence converge or diverge? Justify your answer. Consider the sequence below: 345 2. 4' 9' 16' ·} (a) Express this sequence in the form {a}1 (b) Does this sequence converge or diverge? Justify your answer.arrow_forward
- Use the growth rate of sequences theorem to find the limit or state it divergesarrow_forwardcalculate the maximum value of the directional derivativearrow_forward2. A tank with a capacity of 650 gal. originally contains 200 gal of water with 100 lb. of salt in solution. Water containing 1 lb. of salt per gallon is entering at a rate of 4 gal/min, and the mixture is allowed to flow out of the tank at a rate of 3 gal/min. a. Find the amount of salt in the tank at any time prior to the instant when the tank begins to overflow (650 gallons). b. Find the concentration (in pounds per gallon) of salt in the tank when the tank hits 400 gallons. D.E. for mixture problems: dv dt=11-12 dA A(t) dtarrow_forward
arrow_back_ios
SEE MORE QUESTIONS
arrow_forward_ios
Recommended textbooks for you
Calculus: Early TranscendentalsCalculusISBN:9781285741550Author:James StewartPublisher:Cengage Learning
Thomas' Calculus (14th Edition)CalculusISBN:9780134438986Author:Joel R. Hass, Christopher E. Heil, Maurice D. WeirPublisher:PEARSON
Calculus: Early Transcendentals (3rd Edition)CalculusISBN:9780134763644Author:William L. Briggs, Lyle Cochran, Bernard Gillett, Eric SchulzPublisher:PEARSON
Calculus: Early TranscendentalsCalculusISBN:9781319050740Author:Jon Rogawski, Colin Adams, Robert FranzosaPublisher:W. H. Freeman
Calculus: Early Transcendental FunctionsCalculusISBN:9781337552516Author:Ron Larson, Bruce H. EdwardsPublisher:Cengage Learning
Calculus: Early Transcendentals
Calculus
ISBN:9781285741550
Author:James Stewart
Publisher:Cengage Learning
Thomas' Calculus (14th Edition)
Calculus
ISBN:9780134438986
Author:Joel R. Hass, Christopher E. Heil, Maurice D. Weir
Publisher:PEARSON
Calculus: Early Transcendentals (3rd Edition)
Calculus
ISBN:9780134763644
Author:William L. Briggs, Lyle Cochran, Bernard Gillett, Eric Schulz
Publisher:PEARSON
Calculus: Early Transcendentals
Calculus
ISBN:9781319050740
Author:Jon Rogawski, Colin Adams, Robert Franzosa
Publisher:W. H. Freeman
Calculus: Early Transcendental Functions
Calculus
ISBN:9781337552516
Author:Ron Larson, Bruce H. Edwards
Publisher:Cengage Learning
What is a Relation? | Don't Memorise; Author: Don't Memorise;https://www.youtube.com/watch?v=hV1_wvsdJCE;License: Standard YouTube License, CC-BY
RELATIONS-DOMAIN, RANGE AND CO-DOMAIN (RELATIONS AND FUNCTIONS CBSE/ ISC MATHS); Author: Neha Agrawal Mathematically Inclined;https://www.youtube.com/watch?v=u4IQh46VoU4;License: Standard YouTube License, CC-BY