Applied Statics and Strength of Materials (6th Edition)
6th Edition
ISBN: 9780133840544
Author: George F. Limbrunner, Craig D'Allaird, Leonard Spiegel
Publisher: PEARSON
expand_more
expand_more
format_list_bulleted
Concept explainers
Videos
Textbook Question
Chapter 15, Problem 15.40P
For Problems 15.31 through 15.43, use the moment-area method.
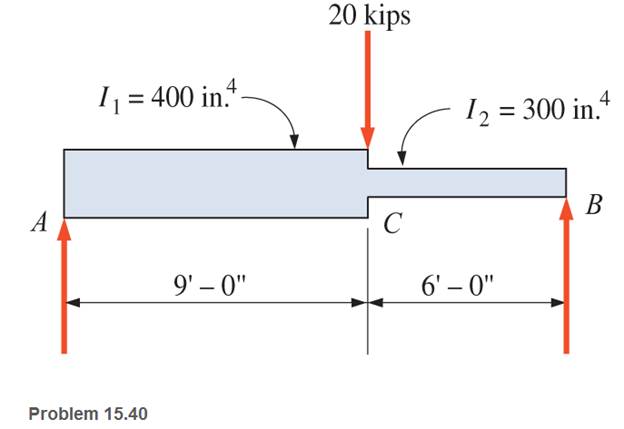
15.40 Calculate the maximum deflection for the simply supported steel beam shown. Neglect the weight of the beam.
Expert Solution & Answer
Want to see the full answer?
Check out a sample textbook solution
Students have asked these similar questions
(use EI constant for whole span). A 10-meter-span, propped beam (fixed at the left support and roller at right support), with a uniformly distributed load from left support to six meters to the right, with a magnitude of six kilonewton per lineal meter, a downward concentrated load at the midspan. Solve the reactions at the fixed support and roller support, slope and deflection at the roller support, using Area Moment Method. Use the concentrated load as 24 kN.
Calculate the slope at C using ONE of these methods: double integration method, area-moment and conjugate beam method. Also,
determine the deflection at C using EITHER virtual work method or Castigliano theorem method. Set P = 10 kN, w = 2 kN/m, support
A is pin and support B is roller.
...
1 m
Compute the slopes at A and C and the deflection at D for the beam shown in Q.2. Also, locate and compute the magnitude of the maximum deflection.
Chapter 15 Solutions
Applied Statics and Strength of Materials (6th Edition)
Ch. 15 - A 14 in.-diameter aluminum rod is bent into a...Ch. 15 - 15.2 Calculate the maximum bending stress produced...Ch. 15 - A 500 -mm-long steel bar having a cross section of...Ch. 15 - 15.4 An aluminum wire has a diameter of in....Ch. 15 - 15.5 A -in.-wide by in.-thick board is bent to a...Ch. 15 - 15.6 A Douglas fir beam is in. wide and in. deep....Ch. 15 - Prob. 15.7PCh. 15 - For Problems 15.7 through 15.14, use the formula...Ch. 15 - For Problems 15.7 through 15.14, use the formula...Ch. 15 - For Problems 15.7 through 15.14, use the formula...
Ch. 15 - For Problems 15.7 through 15.14, use the formula...Ch. 15 - For Problems 15.7 through 15.I4, use the formula...Ch. 15 - For Problems 15.7 through 15.14, use the formula...Ch. 15 - For Problems 15.7 through 15.14, use the formula...Ch. 15 - For Problems 15.15 through 15.26, use the...Ch. 15 - For Problems 15.15 through 15.26, use the...Ch. 15 - For Problems 15.15 through 15.26, use the...Ch. 15 - For Problems 15.15 through 15.26, use the...Ch. 15 - For Problems 15.15 through 15.26, use the...Ch. 15 - For Problems 15.15 through 15.26, use the...Ch. 15 - For Problems 15.15 through 15.26, use the...Ch. 15 - For Problems 15.15 through 15.26, use the...Ch. 15 - For Problems 15.15 through 15.26, use the...Ch. 15 - For Problems 15.15 through 15.26, use the...Ch. 15 - For Problems 15.15 through 15.26, use the...Ch. 15 - For Problems 15.15 through 15.26, use the...Ch. 15 - 15.27 Draw the moment diagram by parts for the...Ch. 15 - 15.28 Draw the moment diagram by parts for the...Ch. 15 - 15.29 Draw the moment diagram by parts for the...Ch. 15 - 15.30 For the beam shown, draw the conventional...Ch. 15 - For Problems 15.31 through 15.43, use the...Ch. 15 - For Problems 15.31 through 15.43, use the...Ch. 15 - For Problems 15.31 through 15.43, use the...Ch. 15 - For Problems 15.31 through 15.43, use the...Ch. 15 - For Problems 15.31 through 15.43, use the...Ch. 15 - For Problems 15.31 through 15.43, use the...Ch. 15 - For Problems 15.31 through 15.43, use the...Ch. 15 - For Problems 15.31 through 15.43, use the...Ch. 15 - For Problems 15.31 through 15.43, use the...Ch. 15 - For Problems 15.31 through 15.43, use the...Ch. 15 - For Problems 15.31 through 15.43, use the...Ch. 15 - For Problems 15.31 through 15.43, use the...Ch. 15 - For Problems 15.31 through 15.43, use the...Ch. 15 - 15.49 If the elastic limit of a steel wire is...Ch. 15 - 15.50 Calculate the bending moment required to...Ch. 15 - 15.51 A 6-ft-long cantilever beam is subjected to...Ch. 15 - 15.52 A structural steel wide-flange section is...Ch. 15 - 15.53 A simply supported structural steel...Ch. 15 - 15.54 A structural steel wide-flange shape is...Ch. 15 - A solid, round simply supported steel shaft is...Ch. 15 - Using the moment-area method, check the...Ch. 15 - 15.57 A 1-in.-diameter steel bar is 25 ft long and...Ch. 15 - 15.58 A 102-mm nominal diameter standard-weight...Ch. 15 - I 5.59 Compute the maximum deflection for the...Ch. 15 - An 8-in-wide by 12-in-deep redwood timber beam...Ch. 15 - 15.61 A solid steel shaft 3 in. in diameter and 20...Ch. 15 - 15.62 For the beam shown, draw the conventional...Ch. 15 - 15.63 Rework Problem 15.62 with concentrated loads...Ch. 15 - 15.64 A solid steel shaft 3 in. in diameter and 20...Ch. 15 - 15.65 A structural steel wide-flange section is...Ch. 15 - 15.66 A 6-in.-by-10-in, hem-fir timber beam (S4S)...Ch. 15 - 15.67 A simply supported structural steel...Ch. 15 - Calculate the maximum permissible span length for...Ch. 15 - 15.69 A structural steel wide-flange section 10 ft...Ch. 15 - 15.70 A structural steel wide-flange section...Ch. 15 - 15.71 Determine the deflection at point C and...Ch. 15 - 15.72 Calculate the deflection midway between the...Ch. 15 - 15.73 Derive an expression for the maximum...Ch. 15 - 15.74 Derive an expression for the maximum...
Knowledge Booster
Learn more about
Need a deep-dive on the concept behind this application? Look no further. Learn more about this topic, mechanical-engineering and related others by exploring similar questions and additional content below.Similar questions
- A cantilever beam shown carries a concentrated load of 20 kN at point C. Assume constant value of E. Compute the deflection at C. Compute the slope at C. Compute the deflection at B.arrow_forwardA beam of uniform rectangular section 200 mm wide and 300 mm deep is simply supported at its ends. It carries a uniformly distributed load of 9 KN/m run over the entire span of 5 m. if the value of E for the beam material is 1 X 104 N/mm2 , find the slope at the supports and maximum deflection. Give me complete solution based on the given above. Again I need to ask the same question since you gave me a wrong answer before.arrow_forwardA round shaft having a diameter of 32 mm is 700 mm long and carries a 3.0 kN load at its center. If the shaft is steel and simply supported at its ends, compute the deflection at the center.arrow_forward
- 1.Calculate the 2nd moment of area for a beam with a length of 200 mm, a width of 20 mm and a height of 3 mm. 2. For the same beam, and using the provided equations, calculate the maximum deflection if the beam was cantilevered, had a Young's modulus of 207 GPa and had a load of 2.5 N applied at the free end.arrow_forwardFor the cantilever beam shown, calculate the deflections δB at point B, due to the simultaneous action of themoment M0 and the load P. Use superposition principle.arrow_forwardCalculate the modulus of section of rectangle beam of breadth 120 mm and height 200 mm.arrow_forward
- 3. Calculate the slope and deflection at the 60-kNm couple on the structure shown in the accompanying illustration. Use: a. Moment Area Method, b. Conjugate Beam Method 4 kN/m Fixed Hinge 60 kNm 5 m -5 m 5 m -5m I=1.46 x 10° mm". E=200000MPa Activate Windows so to Settings to activate W ndows.arrow_forwardRefer to the previous problem. Calculate the resulting maximum positive moment (kN-m). O 77.4 O 96.8 O 54.4 O 108.8 SITUATION. A simply supported beam has a span of 12 m. It carries a total uniformly distributed load of 21.5 kN/m. To prevent excessive deflection, a support is added at midspan. Calculate the reaction (kN) at the added support. O 96.75 O 161.25 80.62 O 48.38 PLS ANSWER ASAP THANKSarrow_forwardUsing the double-integration method, find the deflection C and the slope at B. Assume that EI is constant for the beam.arrow_forward
- The cantilever beam is loaded as shown below by a concentrated force ‘P’ and a moment, ‘Mo’. Use the method of superposition to calculate the vertical deflection at the free end due to this loading. Note that ‘A’ the cross-sectional area of the beam, and ‘I’ is the moment of inertia of the cross-section around the bending axis and ‘E’ is the modulus of elasticity of the beam.arrow_forwardPlease draw by deriving SF and BM equations for each sections.Draw a labelled diagram mentioning valus at key points. Thank youarrow_forwardOn a formatted bond paper, copy and solve the problem. Show your neat and detailed solution. Use three (3) decimal places for your answers and enclosed it in a box. Compute the deflection and slope at a section 8 ft from the wall for the beam shown in the figure using Double Integration Method. Assume that E = 28 x 103 psi and 1= 30.75 1200 lb in4. A 800 lb/ft -8 ft -8 ft Barrow_forward
arrow_back_ios
SEE MORE QUESTIONS
arrow_forward_ios
Recommended textbooks for you
Elements Of ElectromagneticsMechanical EngineeringISBN:9780190698614Author:Sadiku, Matthew N. O.Publisher:Oxford University Press
Mechanics of Materials (10th Edition)Mechanical EngineeringISBN:9780134319650Author:Russell C. HibbelerPublisher:PEARSON
Thermodynamics: An Engineering ApproachMechanical EngineeringISBN:9781259822674Author:Yunus A. Cengel Dr., Michael A. BolesPublisher:McGraw-Hill Education
Control Systems EngineeringMechanical EngineeringISBN:9781118170519Author:Norman S. NisePublisher:WILEY
Mechanics of Materials (MindTap Course List)Mechanical EngineeringISBN:9781337093347Author:Barry J. Goodno, James M. GerePublisher:Cengage Learning
Engineering Mechanics: StaticsMechanical EngineeringISBN:9781118807330Author:James L. Meriam, L. G. Kraige, J. N. BoltonPublisher:WILEY
Elements Of Electromagnetics
Mechanical Engineering
ISBN:9780190698614
Author:Sadiku, Matthew N. O.
Publisher:Oxford University Press
Mechanics of Materials (10th Edition)
Mechanical Engineering
ISBN:9780134319650
Author:Russell C. Hibbeler
Publisher:PEARSON
Thermodynamics: An Engineering Approach
Mechanical Engineering
ISBN:9781259822674
Author:Yunus A. Cengel Dr., Michael A. Boles
Publisher:McGraw-Hill Education
Control Systems Engineering
Mechanical Engineering
ISBN:9781118170519
Author:Norman S. Nise
Publisher:WILEY
Mechanics of Materials (MindTap Course List)
Mechanical Engineering
ISBN:9781337093347
Author:Barry J. Goodno, James M. Gere
Publisher:Cengage Learning
Engineering Mechanics: Statics
Mechanical Engineering
ISBN:9781118807330
Author:James L. Meriam, L. G. Kraige, J. N. Bolton
Publisher:WILEY
Solids: Lesson 53 - Slope and Deflection of Beams Intro; Author: Jeff Hanson;https://www.youtube.com/watch?v=I7lTq68JRmY;License: Standard YouTube License, CC-BY