Chapter 14.3, Problem 22E

a.

To determine

To calculate: The median of the number of women’s teams playing a sport .

Answer to Problem 22E

The median is $282$ .

Explanation of Solution

Given information:

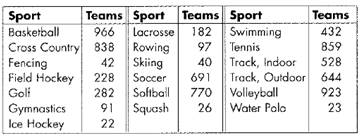
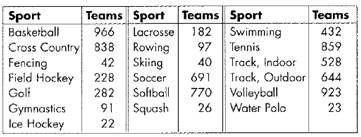
During a season, 7684n teams played 19 NCAA women’s sports.

  

Formula used:

Median for even terms = $\frac{{\left(\frac{n}{2}\right)}^{th}\text{term}+{\left(\frac{n}{2}+1\right)}^{th}\text{term}}{2}$

Median for odd terms = ${\left(\frac{n+1}{2}\right)}^{th}\text{term}$

Calculation:

Consider the data in ascending order ,

  $\left\{22,23,26,40,42,91,97,182,228,282,432,528,644,691,770,838,859,923,966\right\}.$

Since there are seven rivers. So, $n=19$ .

There is odd number of data.

The median of odd number of data is −

  $\begin{array}{l}={\left(\frac{19+1}{2}\right)}^{th}\text{term}\\ \text{=}{\left(\frac{20}{2}\right)}^{th}\text{term}\\ ={10}^{th}\text{term}\\ =282\end{array}$

Hence, the median is $282$ .

b.

To determine

To calculate: The first quartile point and the third quartile point.

Answer to Problem 22E

The first quartile and third quartile are $\text{42 and 770 respectively}\text{.}$

Explanation of Solution

Given information:

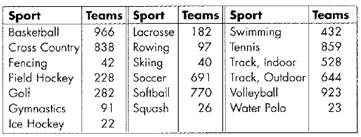
During a season, 7684n teams played 19 NCAA women’s sports.

  

Formula used:

If each group has the median, the data is divided into four groups. Each group is called quartile.

Median for even terms = $\frac{{\left(\frac{n}{2}\right)}^{th}\text{term}+{\left(\frac{n}{2}+1\right)}^{th}\text{term}}{2}$

Median for odd terms = ${\left(\frac{n+1}{2}\right)}^{th}\text{term}$

Calculation:

Consider the data in ascending order ,

  $\left\{22,23,26,40,42,91,97,182,228,282,432,528,644,691,770,838,859,923,966\right\}.$

Since there are seven rivers. So, $n=19$ .

There is odd number of data.

The median of odd number of data is −

  $\begin{array}{l}={\left(\frac{19+1}{2}\right)}^{th}\text{term}\\ \text{=}{\left(\frac{20}{2}\right)}^{th}\text{term}\\ ={10}^{th}\text{term}\\ =282\end{array}$

Therefore , the data is divided into two parts.

Lower half - $22,23,26,40,42,91,97,182,228.$ and

Upper half - $432,528,644,691,770,838,859,923,966.$

Median of lower half is −

  $\begin{array}{l}={\left(\frac{9+1}{2}\right)}^{th}\text{term}\\ ={\left(\frac{10}{2}\right)}^{th}\text{term}\\ ={\left(5\right)}^{th}\text{term}\\ =42\end{array}$

Median of upper half is −

  $\begin{array}{l}={\left(\frac{9+1}{2}\right)}^{th}\text{term}\\ ={\left(\frac{10}{2}\right)}^{th}\text{term}\\ ={\left(5\right)}^{th}\text{term}\\ =770\end{array}$

The quartile points are :-

  $\begin{array}{l}{Q}_1=42\\ Q_2=282\\ Q_3=770\end{array}$

Hence, the first quartile and third quartile are $42\text{ and 770 respectively}\text{.}$

c.

To determine

To calculate: The interquartile range and semi-interquartile range.

Answer to Problem 22E

The interquartile range is $728$ and semi-interquartile is $364.$

Explanation of Solution

Given information:

During a season, 7684n teams played 19 NCAA women’s sports.

  

Formula used:

The difference between the first quartile point and third quartile point is called the inter- quartile range.

The inter- quartile range is divided by 2, the quotient is called the semi- interquartile range.

Calculation:

Consider the data in ascending order ,

  $\left\{22,23,26,40,42,91,97,182,228,282,432,528,644,691,770,838,859,923,966\right\}.$

Since there are seven rivers. So, $n=19$ .

There is odd number of data.

The median of odd number of data is $282.$

The quartile points are :-

  $\begin{array}{l}{Q}_1=42\\ Q_2=282\\ Q_3=770\end{array}$

The inter- quartile range is $Q_3-Q_1.$

  $\begin{array}{l}=770-42\\ =728.\end{array}$

The semi-interquartile range -

  $\frac{\text{inter-quartile range}}{2}.$

  $\begin{array}{l}=\frac{728}{2}\\ =364.\end{array}$

Hence, the interquartile range is $728$ and semi-interquartile is $364.$

d.

To determine

To show: whether there is any outliers.

Answer to Problem 22E

No outliers.

Explanation of Solution

Given information:

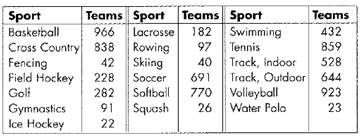
During a season, 7684n teams played 19 NCAA women’s sports.

  

Formula used:

Outliers are extreme values that are more than 1.5 times the interquartile range beyond the upper or lower quartiles .

Calculation:

Consider the data in ascending order ,

  $\left\{22,23,26,40,42,91,97,182,228,282,432,528,644,691,770,838,859,923,966\right\}.$

Since there are seven rivers. So, $n=19$ .

There is odd number of data.

The median of odd number of data is $282.$

The quartile points are :-

  $\begin{array}{l}{Q}_1=42\\ Q_2=282\\ Q_3=770\end{array}$

The inter- quartile range is $728.$

For outlier

  $\begin{array}{l}{Q}_1-1.5\left(728\right)=42-1092=-1050\\ Q_3+1.5\left(728\right)=770+=1092\end{array}$

The lower extreme 22 and the upper extreme 966 are within the limits.

So, there are no outliers.

e.

To determine

To sketch: A box-and-whisker of the number of women’s teams playing a sport.

Explanation of Solution

Given information:

During a season, 7684n teams played 19 NCAA women’s sports.

  

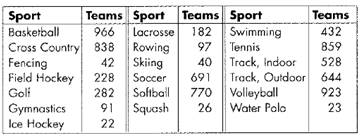
Graph:

  

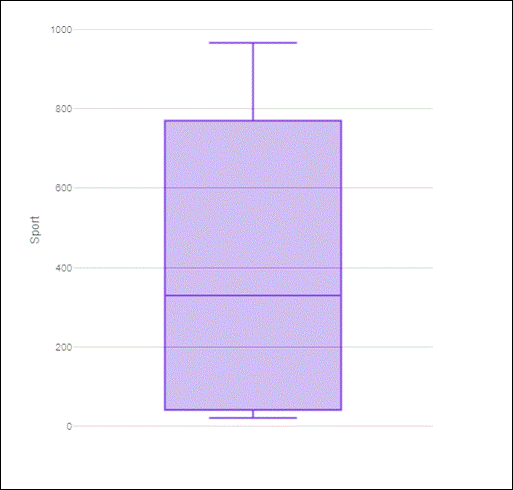
Interpretation:

The vertical graph is known as box-and-whisker plots. It represents the number of women’s teams playing a sport. The median is 282. It does not have outliers.

f.

To determine

To calculate: The mean of the number of women’s teams playing a sport.

Answer to Problem 22E

The mean is $\mathrm{404.42.}$

Explanation of Solution

Given information:

During a season, 7684n teams played 19 NCAA women’s sports.

  

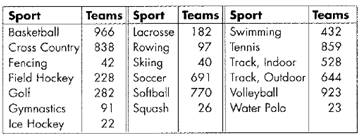
Formula used:

Formula of Mean

  $\overline{X}=\frac{{\displaystyle \sum X}}{n}$ where X represents each of the values in the data set.

Calculation:

Consider the data in ascending order ,

  $\left\{22,23,26,40,42,91,97,182,228,282,432,528,644,691,770,838,859,923,966\right\}.$

Since there are seven rivers. So, $n=19$ .

The mean of the data is

  $\begin{array}{l}=\frac{22+23+26+40+42+91+97+182+228+282+432+528+644+691+770+838+859+923+966}{19}\\ =\frac{7684}{19}\\ =404.42\end{array}$

Hence, the mean is $\mathrm{404.42.}$

g.

To determine

To calculate: The mean deviation of the data.

Answer to Problem 22E

The mean deviation is $\mathrm{316.969.}$

Explanation of Solution

Given information:

During a season, 7684n teams played 19 NCAA women’s sports.

  

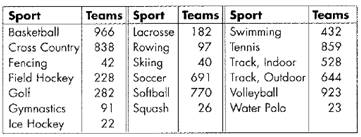
Formula used:

The arithmetic mean of the absolute values of the deviations from the mean of a set of data is called the mean deviation.

  $MD=\frac{1}{n}{\displaystyle \sum _{i=1}^n\left|X_i-\overline{X}\right|}$

Formula of Mean

  $\overline{X}=\frac{{\displaystyle \sum X}}{n}$ where X represents each of the values in the data set.

Calculation:

Consider the data in ascending order ,

  $\left\{22,23,26,40,42,91,97,182,228,282,432,528,644,691,770,838,859,923,966\right\}.$

Since there are seven rivers. So, $n=19$ .

The mean of the data is $\mathrm{404.42.}$

The mean deviation is −

$X_i$	$\overline{X}$	$\left|X_i-\overline{X}\right|$
22	404.42	$\begin{array}{l}=\left|22-404.42\right|\\ =382.42\end{array}$
23	404.42	$\begin{array}{l}=\left|23-404.42\right|\\ =381.42\end{array}$
26	404.42	$\begin{array}{l}=\left|26-404.42\right|\\ =378.42\end{array}$
40	404.42	$\begin{array}{l}=\left|40-404.42\right|\\ =364.42\end{array}$
42	404.42	$\begin{array}{l}=\left|42-404.42\right|\\ =362.42\end{array}$
91	404.42	$\begin{array}{l}=\left|91-404.42\right|\\ =313.42\end{array}$
97	404.42	$\begin{array}{l}=\left|97-404.42\right|\\ =307.42\end{array}$
182	404.42	$\begin{array}{l}=\left|182-404.42\right|\\ =222.42\end{array}$
228	404.42	$\begin{array}{l}=\left|228-404.42\right|\\ =176.42\end{array}$
282	404.42	$\begin{array}{l}=\left|282-404.42\right|\\ =122.42\end{array}$
432	404.42	$\begin{array}{l}=\left|432-404.42\right|\\ =27.58\end{array}$
528	404.42	$\begin{array}{l}=\left|528-404.42\right|\\ =123.58\end{array}$
644	404.42	$\begin{array}{l}=\left|644-404.42\right|\\ =239.58\end{array}$
691	404.42	$\begin{array}{l}=\left|691-404.42\right|\\ =286.58\end{array}$
770	404.42	$\begin{array}{l}=\left|770-404.42\right|\\ =365.58\end{array}$
838	404.42	$\begin{array}{l}=\left|838-404.42\right|\\ =433.58\end{array}$
859	404.42	$\begin{array}{l}=\left|859-404.42\right|\\ =454.58\end{array}$
923	404.42	$\begin{array}{l}=\left|923-404.42\right|\\ =518.58\end{array}$
966	404.42	$\begin{array}{l}=\left|966-404.42\right|\\ =561.58\end{array}$
${\displaystyle \sum _{i=1}^{19}\left|X_i-\overline{X}\right|}$		$6022.42$$$

  $\begin{array}{l}MD=\frac{1}{19}\left(6022.42\right)\\ =316.969\end{array}$

Hence, the mean deviation is $\mathrm{316.969.}$

h.

To determine

To calculate: The variance of the data.

Answer to Problem 22E

The variance is $97461.55$

Explanation of Solution

Given information:

During a season, 7684n teams played 19 NCAA women’s sports.

  

Formula used:

A measure of variability associated with the arithmetic mean is the standard deviation.

  $\sigma =\sqrt{\frac{1}{n}{\displaystyle \sum _{i=1}^n{\left(X_i-\overline{X}\right)}^2}}$

The variance is the mean of the squares of the deviations from $\overline{X}$ .

The standard deviation is the positive square root of the variance.

Calculation:

Consider the data in ascending order ,

  $\left\{22,23,26,40,42,91,97,182,228,282,432,528,644,691,770,838,859,923,966\right\}.$

Since there are seven rivers. So, $n=19$ .

The mean of the data is

  $\begin{array}{l}=\frac{22+23+26+40+42+91+97+182+228+282+432+528+644+691+770+838+859+923+966}{19}\\ =\frac{7684}{19}\\ =404.42\end{array}$

Therefore , the standard deviation is −

$X_i$	$\overline{X}$	$X_i-\overline{X}$	${\left(X_i-\overline{X}\right)}^2$
22	404.42	$\begin{array}{l}=22-404.42\\ =-382.42\end{array}$	$\begin{array}{l}={\left(-382.42\right)}^2\\ =146245.05\end{array}$
23	404.42	$\begin{array}{l}=23-404.42\\ =-381.42\end{array}$	$\begin{array}{l}={\left(-381.42\right)}^2\\ =145481.21\end{array}$
26	404.42	$\begin{array}{l}=26-404.42\\ =-378.42\end{array}$	$\begin{array}{l}={\left(-378.42\right)}^2\\ =143201.69\end{array}$
40	404.42	$\begin{array}{l}=40-404.42\\ =-364.42\end{array}$	$\begin{array}{l}={\left(-364.42\right)}^2\\ =132801.93\end{array}$
42	404.42	$\begin{array}{l}=42-404.42\\ =-362.42\end{array}$	$\begin{array}{l}={\left(-362.42\right)}^2\\ =131348.25\end{array}$
91	404.42	$\begin{array}{l}=91-404.42\\ =-313.42\end{array}$	$\begin{array}{l}={\left(-313.42\right)}^2\\ =98232.09\end{array}$
97	404.42	$\begin{array}{l}=97-404.42\\ =-307.42\end{array}$	$\begin{array}{l}={\left(-307.42\right)}^2\\ =94507.05\end{array}$
182	404.42	$\begin{array}{l}=182-404.42\\ =-222.42\end{array}$	$\begin{array}{l}={\left(-222.42\right)}^2\\ =49470.65\end{array}$
228	404.42	$\begin{array}{l}=228-404.42\\ =-176.42\end{array}$	$\begin{array}{l}={\left(-176.42\right)}^2\\ =31124.01\end{array}$
282	404.42	$\begin{array}{l}=282-404.42\\ =-122.42\end{array}$	$\begin{array}{l}={\left(-122.42\right)}^2\\ =14986.65\end{array}$
432	404.42	$\begin{array}{l}=432-404.42\\ =27.58\end{array}$	$\begin{array}{l}={\left(27.58\right)}^2\\ =760.65\end{array}$
528	404.42	$\begin{array}{l}=528-404.42\\ =123.58\end{array}$	$\begin{array}{l}={\left(123.58\right)}^2\\ =15272.01\end{array}$
644	404.42	$\begin{array}{l}=644-404.42\\ =239.58\end{array}$	$\begin{array}{l}={\left(239.58\right)}^2\\ =57398.57\end{array}$
691	404.42	$\begin{array}{l}=691-404.42\\ =286.58\end{array}$	$\begin{array}{l}={\left(286.58\right)}^2\\ =82128.09\end{array}$
770	404.42	$\begin{array}{l}=770-404.42\\ =365.58\end{array}$	$\begin{array}{l}={\left(365.58\right)}^2\\ =133648.73\end{array}$
838	404.42	$\begin{array}{l}=838-404.42\\ =433.58\end{array}$	$\begin{array}{l}={\left(433.58\right)}^2\\ =187991.61\end{array}$
859	404.42	$\begin{array}{l}=859-404.42\\ =454.58\end{array}$	$\begin{array}{l}={\left(454.58\right)}^2\\ =206642.97\end{array}$
923	404.42	$\begin{array}{l}=923-404.42\\ =518.58\end{array}$	$\begin{array}{l}={\left(518.58\right)}^2\\ =268925.21\end{array}$
966	404.42	$\begin{array}{l}=966-404.42\\ =561.58\end{array}$	$\begin{array}{l}={\left(561.58\right)}^2\\ =315372.09\end{array}$
${\displaystyle \sum _{i=1}^{19}{\left(X_i-\overline{X}\right)}^2}$$$			$=1851769.51$

  $\begin{array}{l}=\sigma =\sqrt{\frac{1}{19}\left(1851769.51\right)}\\ =\sigma =\sqrt{97461.55}\\ ={\sigma }^2={\left(\sqrt{97461.55}\right)}^2\\ ={\sigma }^2=97461.55\end{array}$

Hence, the variance is $97461.55$

i.

To determine

To calculate: The standard deviation of the data.

Answer to Problem 22E

The mean is $\mathrm{404.42.}$

Explanation of Solution

Given information:

During a season, 7684n teams played 19 NCAA women’s sports.

  

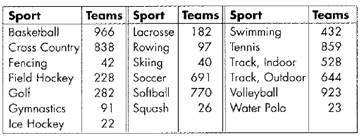
Formula used:

A measure of variability associated with the arithmetic mean is the standard deviation.

  $\sigma =\sqrt{\frac{1}{n}{\displaystyle \sum _{i=1}^n{\left(X_i-\overline{X}\right)}^2}}$

Formula of Mean

  $\overline{X}=\frac{{\displaystyle \sum X}}{n}$ where X represents each of the values in the data set.

Calculation:

Consider the data in ascending order ,

  $\left\{22,23,26,40,42,91,97,182,228,282,432,528,644,691,770,838,859,923,966\right\}.$

Since there are seven rivers. So, $n=19$ .

The mean of the data is

  $\begin{array}{l}=\frac{22+23+26+40+42+91+97+182+228+282+432+528+644+691+770+838+859+923+966}{19}\\ =\frac{7684}{19}\\ =404.42\end{array}$

Therefore , the standard deviation is −

$X_i$	$\overline{X}$	$X_i-\overline{X}$	${\left(X_i-\overline{X}\right)}^2$
22	404.42	$\begin{array}{l}=22-404.42\\ =-382.42\end{array}$	$\begin{array}{l}={\left(-382.42\right)}^2\\ =146245.05\end{array}$
23	404.42	$\begin{array}{l}=23-404.42\\ =-381.42\end{array}$	$\begin{array}{l}={\left(-381.42\right)}^2\\ =145481.21\end{array}$
26	404.42	$\begin{array}{l}=26-404.42\\ =-378.42\end{array}$	$\begin{array}{l}={\left(-378.42\right)}^2\\ =143201.69\end{array}$
40	404.42	$\begin{array}{l}=40-404.42\\ =-364.42\end{array}$	$\begin{array}{l}={\left(-364.42\right)}^2\\ =132801.93\end{array}$
42	404.42	$\begin{array}{l}=42-404.42\\ =-362.42\end{array}$	$\begin{array}{l}={\left(-362.42\right)}^2\\ =131348.25\end{array}$
91	404.42	$\begin{array}{l}=91-404.42\\ =-313.42\end{array}$	$\begin{array}{l}={\left(-313.42\right)}^2\\ =98232.09\end{array}$
97	404.42	$\begin{array}{l}=97-404.42\\ =-307.42\end{array}$	$\begin{array}{l}={\left(-307.42\right)}^2\\ =94507.05\end{array}$
182	404.42	$\begin{array}{l}=182-404.42\\ =-222.42\end{array}$	$\begin{array}{l}={\left(-222.42\right)}^2\\ =49470.65\end{array}$
228	404.42	$\begin{array}{l}=228-404.42\\ =-176.42\end{array}$	$\begin{array}{l}={\left(-176.42\right)}^2\\ =31124.01\end{array}$
282	404.42	$\begin{array}{l}=282-404.42\\ =-122.42\end{array}$	$\begin{array}{l}={\left(-122.42\right)}^2\\ =14986.65\end{array}$
432	404.42	$\begin{array}{l}=432-404.42\\ =27.58\end{array}$	$\begin{array}{l}={\left(27.58\right)}^2\\ =760.65\end{array}$
528	404.42	$\begin{array}{l}=528-404.42\\ =123.58\end{array}$	$\begin{array}{l}={\left(123.58\right)}^2\\ =15272.01\end{array}$
644	404.42	$\begin{array}{l}=644-404.42\\ =239.58\end{array}$	$\begin{array}{l}={\left(239.58\right)}^2\\ =57398.57\end{array}$
691	404.42	$\begin{array}{l}=691-404.42\\ =286.58\end{array}$	$\begin{array}{l}={\left(286.58\right)}^2\\ =82128.09\end{array}$
770	404.42	$\begin{array}{l}=770-404.42\\ =365.58\end{array}$	$\begin{array}{l}={\left(365.58\right)}^2\\ =133648.73\end{array}$
838	404.42	$\begin{array}{l}=838-404.42\\ =433.58\end{array}$	$\begin{array}{l}={\left(433.58\right)}^2\\ =187991.61\end{array}$
859	404.42	$\begin{array}{l}=859-404.42\\ =454.58\end{array}$	$\begin{array}{l}={\left(454.58\right)}^2\\ =206642.97\end{array}$
923	404.42	$\begin{array}{l}=923-404.42\\ =518.58\end{array}$	$\begin{array}{l}={\left(518.58\right)}^2\\ =268925.21\end{array}$
966	404.42	$\begin{array}{l}=966-404.42\\ =561.58\end{array}$	$\begin{array}{l}={\left(561.58\right)}^2\\ =315372.09\end{array}$
${\displaystyle \sum _{i=1}^{19}{\left(X_i-\overline{X}\right)}^2}$$$			$=1851769.51$

  $\begin{array}{l}=\sigma =\sqrt{\frac{1}{19}\left(1851769.51\right)}\\ =\sigma =\sqrt{97461.55}\\ =\sigma =312.188\end{array}$

Hence, the standard deviation is $312.188$

j.

To determine

To discuss: The variability of the data.

Explanation of Solution

Given information:

During a season, 7684n teams played 19 NCAA women’s sports.

  

Summary:

Variability of the data can be studied by box-and-whisker plot.

It represent the median, quartiles, interquartile range , and extreme values in a set of the data.

Terms	7
Median	282
$Q_1$	42
$Q_3$	770
Interquartile	728
Semi-interquartile	364
Outliers	No

Thus, the box-and-whisker drawn in previous part is a pictorial representation of the variability of the data.