Chapter 14.3, Problem 11E

To determine

To calculate: The inter-quartile range and the semi-interquartile range of $\left\{15.1,9.0,8.5,5.8,6.2,8.5,10.5,11.5,8.8,7.6\right\}.$ Also, draw a box-and-whisker plot.

Answer to Problem 11E

Quartile points are $Q_1=7.6,Q_2=8.65,Q_3=\mathrm{10.5.}$

Interquartile range is $2.9$ .

Semi- interquartile range is $\mathrm{1.45.}$

  

Explanation of Solution

Given information:

  $\left\{15.1,9.0,8.5,5.8,6.2,8.5,10.5,11.5,8.8,7.6\right\}.$

Formula used:

If each group has the median, the data is divided into four groups. Each group is called quartile.

The difference between the first quartile point and third quartile point is called the inter- quartile range.

The inter- quartile range is divided by 2, the quotient is called the semi- interquartile range.

Median for even terms = $\frac{{\left(\frac{n}{2}\right)}^{th}\text{term}+{\left(\frac{n}{2}+1\right)}^{th}\text{term}}{2}$

Median for odd terms = ${\left(\frac{n+1}{2}\right)}^{th}\text{term}$

Calculation:

Re-arranging the data in ascending order ,

  $5.8,6.2,7.6,8.5,8.5,8.8,9.0,10.5,11.5,15.1$

Since , the number of terms are $n=10$ .

So, the median is

  $\begin{array}{l}=\frac{{\left(\frac{10}{2}\right)}^{th}\text{term}+{\left(\frac{10}{2}+1\right)}^{th}\text{term}}{2}\\ =\frac{{\left(5\right)}^{th}\text{term}+{\left(6\right)}^{th}\text{term}}{2}\\ =\frac{8.5+8.8}{2}\\ =\frac{17.3}{2}\\ =8.65\end{array}$

Therefore , the data is divided into two parts.

Lower half - $5.8,6.2,7.6,8.5,8.5$ and Upper half - $8.8,9.0,10.5,11.5,15.1$

Median of lower half is −

  $\begin{array}{l}={\left(\frac{5+1}{2}\right)}^{th}\text{term}\\ ={\left(\frac{6}{2}\right)}^{th}\text{term}\\ ={\left(3\right)}^{rd}\text{term}\\ =7.6\end{array}$

Median of upper half is −

  $\begin{array}{l}={\left(\frac{5+1}{2}\right)}^{th}\text{term}\\ ={\left(\frac{6}{2}\right)}^{th}\text{term}\\ ={\left(3\right)}^{rd}\text{term}\\ =10.5\end{array}$

The quartile points are :-

  $\begin{array}{l}{Q}_1=7.6\\ Q_2=8.65\\ Q_3=10.5\end{array}$

The inter- quartile range is $Q_3-Q_1.$

  $\begin{array}{l}=10.5-7.6\\ =2.9\end{array}$

The semi-interquartile range -

  $\frac{\text{inter-quartile range}}{2}.$

  $\begin{array}{l}=\frac{2.9}{2}\\ =\mathrm{1.45.}\end{array}$

Hence, the Quartile points are $Q_1=7.6,Q_2=8.65,Q_3=\mathrm{10.5.}$ The interquartile range is $2.9$ and semi- interquartile range is $\mathrm{1.45.}$

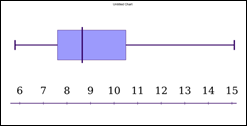
Now, using above data , sketch a box-and-whisker plot.

  

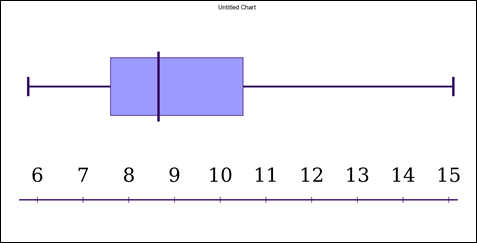
The graph represents the quartile points with median at 22.