Chapter 1.4, Problem 62E

(a)

To determine

The maximum profit for various numbers of units ordered.

Answer to Problem 62E

It is a fair estimate that the maximum profit from the sales is 3375$

Explanation of Solution

Given information:

Consider the following table,

  

Where x is the number of units and P is the profit from them.

Formula used:

The maximum profit value is taken from the table P.

Calculation:

To estimate the maximum profit from the table compare the values of P among them. This gives,

  $\begin{array}{l}x=150\\ y=3375\end{array}$

Therefore it is a fair estimate that the maximum profit from the sales is 3375$

Conclusion:

The maximum profit from the sales is 3375$

(b)

To determine

The relation defined by the ordered pairs represents P as a function of X.

Answer to Problem 62E

As no single value in x-axis is related to more than one element in y-axishence, this relation is a function.

Explanation of Solution

Given information:

Consider the following table,

  

Where x is the number of units and P is the profit from them.

Formula used:

The x value is plotted along the horizontal axis and P value is plotted along the vertical axis.

Calculation:

A graphical plot is prepared taking x along the x-axis and P along the y-axis.

  

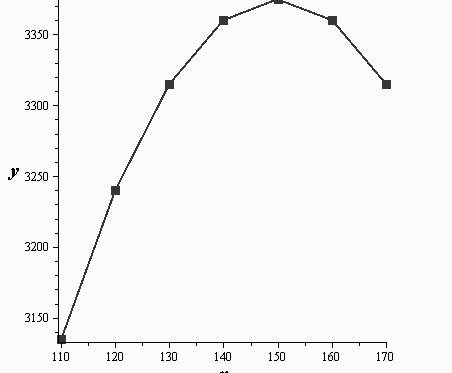
As no single value in x-axis is related to more than one element in y-axis. Hence, this relation is a function.

Conclusion:

The graph has the value that increases continuously and then decreases.

(c)

To determine

The domain of the function.

Answer to Problem 62E

As the number of units sold cannot be less than 0, the domain 0f the function is $\left(0,\infty \right)$

Explanation of Solution

Given information:

Consider the following table,

  

Where x is the number of units and P is the profit from them.

Formula used:

  $P=\left[\left(90\times 100\right)+\left(x-100\right)\times \left(90-0.15\right)\right]-\left(x\times 60\right);x\ge 100$

Calculation:

Consider the following data;

Cost price up to 100 units is $60/unit,

Above 100, cost price per unit is reduced by $0.15 for each extra unit purchased,

Selling price is $90/unit.

Assume x be the number of units sold. So,

  $P=\left[\left(90\times 100\right)+\left(x-100\right)\times \left(90-0.15\right)\right]-\left(x\times 60\right);x\ge 100$

Simplifying it further,

  $\begin{array}{l}P=\left[\left(900\times 100\right)+\left(x-100\right)\times \left(90-0.15\right)\right]-\left(x\times 60\right)\\ =\left[9000+\left(x-100\right)\times 89.85\right]-60x\\ =89.85x+15-60x\\ P=29.85x+15x\ge 100\end{array}$

Next

  $\begin{array}{l}P=x\times 90-x\times 60x<100\\ P=30x\end{array}$

As the number of units sold cannot be less than 0, the domain 0f the function is $\left(0,\infty \right)$

Conclusion:

The domain 0f the function is $\left(0,\infty \right)$