
a.
To calculate: the total duration of the voyage in hours
a.
Answer to Problem 7PS
Total time
Explanation of Solution
Given:
At 2:000 P.M. on April 11, 1912, the Titanic left Cobh, Ireland, on her voyage to New York City. At 11:40 P.M. on April 14, the Titanic struck an iceberg and sank, having covered only about 2100 miles of the approx. 3400-mile trip.
Calculation:
From 2:000 P.M. in April 11, to 11:40 P.M. on April 14, total time is 3 days, 9 hours, and 40 minutes.
1 day = 24 hours and 1 minute
So total time will be
b.
To calculate: the average speed in miles per hour
b.
Answer to Problem 7PS
Average speed
Explanation of Solution
Given:
At 2:000 P.M. in April 11, 1912, the Titanic left Cobh, Ireland, on her voyage to New York City. At 11:40 P.M. on April 14, the Titanic struck an iceberg and sank, having covered only about 2100 miles of the approx. 3400-mile trip.
Concept used:
Average speed
Calculation:
Average speed
c.
To calculate: the domain and range of the function and write a function relating the distance from New York City and the number of hours traveled.
c.
Answer to Problem 7PS
Domain of the function is
Range of function is
The function related to distance is
Explanation of Solution
Given:
At 2:000 P.M. in April 11, 1912, the Titanic left Cobh, Ireland, on her voyage to New York City. At 11:40 P.M. on April 14, the Titanic struck an iceberg and sank, having covered only about 2100 miles of the approx. 3400-mile trip.
From above parts we the total duration of journey is
Calculation:
First we find the domain.
Let x represent the total time in hours.
Since total duration of journey is
Now we find the range,
Given: Distance of journey = 3400 mile
Distance of ship from Ireland = 2100 miles
Let distance of ship from New York = y
Then, Distance of ship from New York = Distance of journey - Distance of ship from Ireland
=3400-2100
=1300 miles
At the time of collision,
As the minimum value of y is 1300 and maximum value of y is 3400. So,
Range of function is
Now we find the equation of the line passing through
Using two point form of straight line,
d.
To plot: the function in part (c).
d.
Answer to Problem 7PS
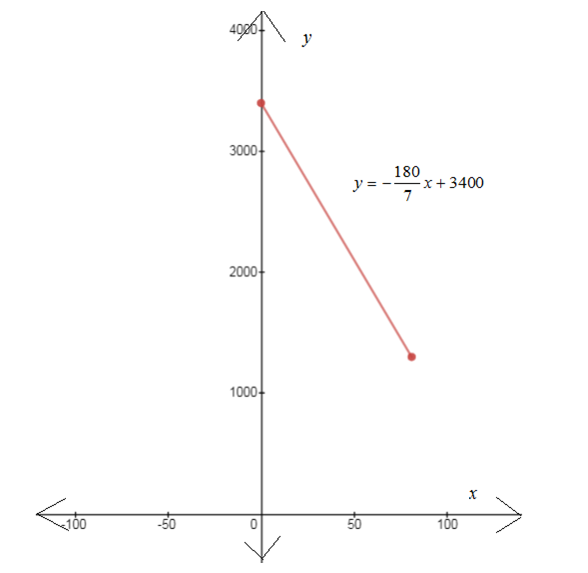
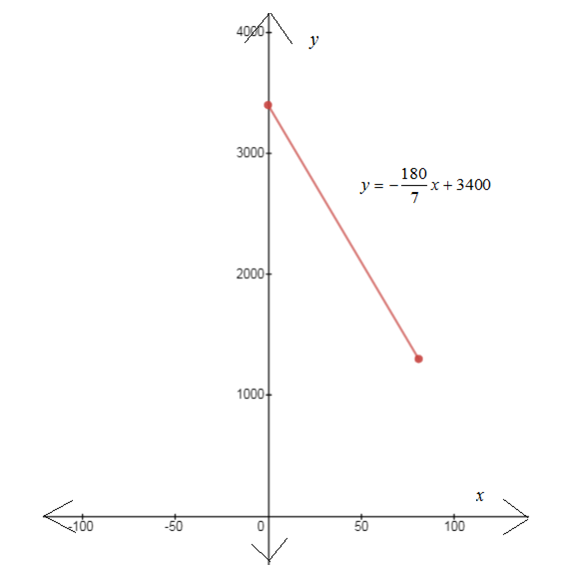
Explanation of Solution
Given:
At 2:000 P.M. in April 11, 1912, the Titanic left Cobh, Ireland, on her voyage to New York City. At 11:40 P.M. on April 14, the Titanic struck an iceberg and sank, having covered only about 2100 miles of the approx. 3400-mile trip.
The function from the above part is
Calculation:
For graph plot the starting point
Chapter 1 Solutions
EBK PRECALCULUS W/LIMITS
- 4. AP CalagaBourd Ten the g stem for 00 3B Quiz 3. The point P has polar coordinates (10, 5). Which of the following is the location of point P in rectangular coordinates? (A) (-5√3,5) (B) (-5,5√3) (C) (5√3,5) (D) (5√3,-5) 7A 6 2 3 4 S 元 3 داند 4/6 Polar axis -0 11 2 3 4 4 5л 3 Зл 2 11π 6 rectangular coordinates of K? The figure shows the polar coordinate system with point P labeled. Point P is rotated an angle of measure clockwise about the origin. The image of this transformation is at the location K (not shown). What are the (A) (-2,2√3) (B) (-2√3,2) (C) (2,-2√3) D) (2√3,-2) T 2arrow_forwardAP CollegeBoard 3B Quiz 1. 2. y AP PRECALCULUS Name: od to dove (or) slog mig Test Boc 2л The figure gives the graphs of four functions labeled A, B, C, and D -1 in the xy-plane. Which is the graph of f(x) = 2 cos¹x ? m -3 π y 2- 1 3 (A) A (B) B 2 A B C D D -1- -2- Graph of f -2 -1 3. 2- y' Graph of g 1 2 1 3 y = R 2/01 y = 1 + 1/2 2 3 4 5 y= = 1-777 2 (C) C (D) D Which of the following defines g(x)? The figure gives the graphs of the functions ƒ and g in the xy-plane. The function f is given by f(x) = tan-1 EVES) (A) (A) tan¹x+1 (B) tan¹ x + 1/ (C) tan¹ (2) +1 (D) tan¹() + (B) Vs) a I.arrow_forwardConsider the region below f(x) = (11-x), above the x-axis, and between x = 0 and x = 11. Let x; be the midpoint of the ith subinterval. Complete parts a. and b. below. a. Approximate the area of the region using eleven rectangles. Use the midpoints of each subinterval for the heights of the rectangles. The area is approximately square units. (Type an integer or decimal.)arrow_forward
- Rama/Shutterstock.com Romaset/Shutterstock.com The power station has three different hydroelectric turbines, each with a known (and unique) power function that gives the amount of electric power generated as a function of the water flow arriving at the turbine. The incoming water can be apportioned in different volumes to each turbine, so the goal of this project is to determine how to distribute water among the turbines to give the maximum total energy production for any rate of flow. Using experimental evidence and Bernoulli's equation, the following quadratic models were determined for the power output of each turbine, along with the allowable flows of operation: 6 KW₁ = (-18.89 +0.1277Q1-4.08.10 Q) (170 - 1.6 · 10¯*Q) KW2 = (-24.51 +0.1358Q2-4.69-10 Q¹²) (170 — 1.6 · 10¯*Q) KW3 = (-27.02 +0.1380Q3 -3.84-10-5Q) (170 - 1.6-10-ºQ) where 250 Q1 <1110, 250 Q2 <1110, 250 <3 < 1225 Qi = flow through turbine i in cubic feet per second KW = power generated by turbine i in kilowattsarrow_forwardHello! Please solve this practice problem step by step thanks!arrow_forwardHello, I would like step by step solution on this practive problem please and thanks!arrow_forward
- Hello! Please Solve this Practice Problem Step by Step thanks!arrow_forwarduestion 10 of 12 A Your answer is incorrect. L 0/1 E This problem concerns hybrid cars such as the Toyota Prius that are powered by a gas-engine, electric-motor combination, but can also function in Electric-Vehicle (EV) only mode. The figure below shows the velocity, v, of a 2010 Prius Plug-in Hybrid Prototype operating in normal hybrid mode and EV-only mode, respectively, while accelerating from a stoplight. 1 80 (mph) Normal hybrid- 40 EV-only t (sec) 5 15 25 Assume two identical cars, one running in normal hybrid mode and one running in EV-only mode, accelerate together in a straight path from a stoplight. Approximately how far apart are the cars after 15 seconds? Round your answer to the nearest integer. The cars are 1 feet apart after 15 seconds. Q Search M 34 mlp CHarrow_forwardFind the volume of the region under the surface z = xy² and above the area bounded by x = y² and x-2y= 8. Round your answer to four decimal places.arrow_forward
- У Suppose that f(x, y) = · at which {(x, y) | 0≤ x ≤ 2,-x≤ y ≤√x}. 1+x D Q Then the double integral of f(x, y) over D is || | f(x, y)dxdy = | Round your answer to four decimal places.arrow_forwardD The region D above can be describe in two ways. 1. If we visualize the region having "top" and "bottom" boundaries, express each as functions of and provide the interval of x-values that covers the entire region. "top" boundary 92(x) = | "bottom" boundary 91(x) = interval of values that covers the region = 2. If we visualize the region having "right" and "left" boundaries, express each as functions of y and provide the interval of y-values that covers the entire region. "right" boundary f2(y) = | "left" boundary fi(y) =| interval of y values that covers the region =arrow_forwardFind the volume of the region under the surface z = corners (0,0,0), (2,0,0) and (0,5, 0). Round your answer to one decimal place. 5x5 and above the triangle in the xy-plane witharrow_forward
 Calculus: Early TranscendentalsCalculusISBN:9781285741550Author:James StewartPublisher:Cengage Learning
Calculus: Early TranscendentalsCalculusISBN:9781285741550Author:James StewartPublisher:Cengage Learning Thomas' Calculus (14th Edition)CalculusISBN:9780134438986Author:Joel R. Hass, Christopher E. Heil, Maurice D. WeirPublisher:PEARSON
Thomas' Calculus (14th Edition)CalculusISBN:9780134438986Author:Joel R. Hass, Christopher E. Heil, Maurice D. WeirPublisher:PEARSON Calculus: Early Transcendentals (3rd Edition)CalculusISBN:9780134763644Author:William L. Briggs, Lyle Cochran, Bernard Gillett, Eric SchulzPublisher:PEARSON
Calculus: Early Transcendentals (3rd Edition)CalculusISBN:9780134763644Author:William L. Briggs, Lyle Cochran, Bernard Gillett, Eric SchulzPublisher:PEARSON Calculus: Early TranscendentalsCalculusISBN:9781319050740Author:Jon Rogawski, Colin Adams, Robert FranzosaPublisher:W. H. Freeman
Calculus: Early TranscendentalsCalculusISBN:9781319050740Author:Jon Rogawski, Colin Adams, Robert FranzosaPublisher:W. H. Freeman
 Calculus: Early Transcendental FunctionsCalculusISBN:9781337552516Author:Ron Larson, Bruce H. EdwardsPublisher:Cengage Learning
Calculus: Early Transcendental FunctionsCalculusISBN:9781337552516Author:Ron Larson, Bruce H. EdwardsPublisher:Cengage Learning





