
Concept explainers
At an amusement park, there are 200-kg bumper cars A, B, and C that have riders with masses of 40 kg, 60 kg, and 35 kg, respectively. Car A is moving to the right with a velocity vA = 2 m/s and car C has a velocity vB = 1.5 m/s to the left, but car B is initially at rest. The coefficient of restitution between each car is 0.8. Determine the final velocity of each car, after all impacts, assuming (a) cars A and C hit car B at the same time, (b) car A hits car B before car C does.
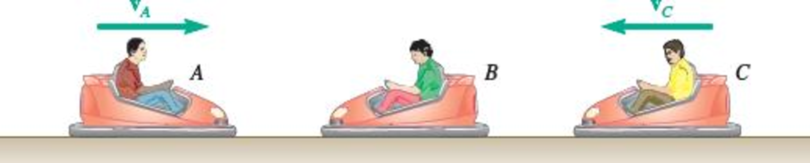
(a)
Find the final velocity of each car after all impact, assuming car A
Answer to Problem 13.162P
The final velocity of each car after all impact, assuming car A
Explanation of Solution
Given information:
The mass of the bumper car (m) is
The mass of the rider A
The mass of the rider B
The mass of the rider C
The velocity of A
The velocity of C
The coefficient of restitution between each car (e) is 0.8.
Calculation:
Calculate the total mass of car A along with rider
Substitute
Calculate the total mass of the car B along with rider
Substitute
Calculate the total mass of the car C along with rider
Substitute
Assume the velocities towards the right to be positive and the velocities towards the left to be negative.
The velocity will be zero as the car B
The expression for the principle of conservation of momentum to the cars A, B, and C when cars A and C hit the car B at the same time as follows;
Here,
Substitute
Calculate the coefficient of restitution (e) of the impact between the cars A and B using the formula:
Substitute 0.8 for e,
Calculate the coefficient of restitution
Substitute 0.8 for e,
Solve the equations (1) and (2) and (3) to obtain velocities.
Add the equations (2) and (3) to eliminate
Multiply the equation (2) with 260 and subtract it from the equation (1).
Multiply the equations (4) with 500 and add it to the equation (5) to obtain the final velocity of the car C.
Substitute
Substitute
Therefore, the final velocity of each car after all impact, assuming car A
(b)
Find the final velocity of each car after all impact, assuming car A
Answer to Problem 13.162P
The final velocity of each car after all impact, assuming car A
Explanation of Solution
Given information:
The mass of the bumper car (m) is
The mass of the rider A
The mass of the rider B
The mass of the rider C
The velocity of A
The velocity of B
The coefficient of restitution between each car (e) is 0.8.
Calculation:
Calculate the final velocities of the cars when car A hits car B before car C does.
The expression for the principle of conservation of momentum to the first impact between car A and car B as follows:
Substitute
Calculate the coefficient of restitution (e) of the first impact between the cars A and B using the formula:
Substitute 0.8 for e,
Multiply the equations (7) with 240 and add it to the equation (6) to obtain the final velocity of car B.
Substitute
The expression for the principle of conservation of momentum for the second impact between car B and car C as follows:
Here, the final velocity of the car B after the second impact is
Substitute
The expression for the coefficient of restitution
Substitute 0.8 for e,
Multiply the equation (9) with 260 and add it to the equation (8) to obtain the final velocity of car C after the impact.
Substitute
Consider the car A and car B again impact with each other.
The expression for the principle of conservation of momentum to the third impact between the car A and car B as follows;
Here,
Substitute
Calculate the coefficient of restitution (e) of the third impact between the cars A and B using the formula:
Substitute 0.8 for e,
Multiply the equation (11) with 240 and add it to the equation (1) to obtain the final velocity of the car B.
Substitute
Therefore, the final velocity of each car after all impact, assuming car A
Want to see more full solutions like this?
Chapter 13 Solutions
<LCPO> VECTOR MECH,STAT+DYNAMICS
- question 664 thank youarrow_forward13.38 Consider the attic of a home located in a hot climate. The floor of the attic is characterized by a width of L₁ = 8 m while the roof makes an angle of 0 = 30° from the horizontal direction, as shown in the schematic. The homeowner wishes to reduce the heat load to the home by adhering bright aluminum foil (ε = 0.07) onto the surfaces of the attic space. Prior to installation of the foil, the surfaces are of emissivity & = 0.90. Attic A2, 82, T2 0 = 30° A1, E1, T₁ 土 L₁ = 8 m (a) Consider installation on the bottom of the attic roof only. Determine the ratio of the radiation heat transfer after to before the installation of the foil. (b) Determine the ratio of the radiation heat transfer after to before installation if the foil is installed only on the top of the attic floor. (c) Determine the ratio of the radiation heat transfer if the foil is installed on both the roof bottom and the floor top.arrow_forward13.1 Determine F2 and F2 for the following configura- tions using the reciprocity theorem and other basic shape factor relations. Do not use tables or charts. (a) Small sphere of area A, under a concentric hemi- sphere of area A₂ = 3A₁ A₂ A1 (a) (b) Long duct. Also, what is F₁₂? A₂ Αν (b) (c) Long inclined plates (point B is directly above the center of A₁) B 100 mm A₂ - 220 mm (c) (d) Long cylinder lying on infinite plane + A₁ Az (d) (e) Hemisphere-disk arrangement -A₂, hemisphere, diameter D A₂ A₁, disk, diameter D/2 (e) (f) Long, open channel 1 m AA₂ 2 m (f) (g) Long cylinders with A₁ = 4A₁. Also, what is F₁₂? -D₁ A1 -A₂ -D2 (e) (h) Long, square rod in a long cylinder. Also, what is F22? w=D/5 18 A₁ -A2 (h) -Darrow_forward
- 13.9 Determine the shape factor, F12, for the rectangles shown. 6 m 1 3 m 6 m 1 m 2 6 m 1 0.5 m 2 1 m (a) Perpendicular rectangles without a common edge. -1 m. (b) Parallel rectangles of unequal areas.arrow_forwardI keep getting the wrong answer i have gotten 6519.87 and 319.71arrow_forwardthank you for previous answer I apologize if the acceleration was unclear it is underlined now along with values in tablesarrow_forward
- ११११११११ TABLE Much 160,000kg Croll 0,005 CD Ap Par ng При nchs 0.15 5m² 1.2kg/m³ 0.98 0.9 0,98 0,9 0,88 IF 20 10 to add The train is going to make several stops along its journey. It will be important for the train to accelerate quickdy to get back up to speed. In order to get Tesla Model S motors until we get the combined The Forque and power needed we are goins bined power and forque needed to accelerate from 0 to 324 km/hr in less than 5 Minutes. Tesla Prated 270 kW Tesla Trated Twheel ng Jaxle 440 NM 20 8.5kgm² 0.45M a) What is the minimum whole number of Tesla Motors required to achieve accelerate the train from 0 to 324 km/hr in less than 5 Nnutes? Seperate the acceleration into constant torque and constant power 0. b) How long does it take the train to accelerate from 0 to 324 km/hr with the number of Tesla motors from part a? c) Using Matlab plot the relocity profile as a function of time, Is this a constant acceleration profile? Barrow_forwardExample find f(t)? -4s F(s)= (s² + 4)²arrow_forwarddraw a kinematic diagramarrow_forward
- Rigid bodies ENG2016. Full complete solutions need okk don't use guidelines but solve full accurate steps by steps don't use chat gpt or any other ai okkk just solve complete solutions okkk take your time but solve complete solutionsarrow_forwardQuestion 6 I need to show all work step by step dynamicsarrow_forwardQu. 3 The automobile is originally at rest s = 0. If it then starts to increase its speed at i = (0.05t2)ft/s?, where t is in seconds, determine the magnitudes of its velocity and acceleration at s = 550 ft. please show all work from dynamics step by step formulaarrow_forward
 Elements Of ElectromagneticsMechanical EngineeringISBN:9780190698614Author:Sadiku, Matthew N. O.Publisher:Oxford University Press
Elements Of ElectromagneticsMechanical EngineeringISBN:9780190698614Author:Sadiku, Matthew N. O.Publisher:Oxford University Press Mechanics of Materials (10th Edition)Mechanical EngineeringISBN:9780134319650Author:Russell C. HibbelerPublisher:PEARSON
Mechanics of Materials (10th Edition)Mechanical EngineeringISBN:9780134319650Author:Russell C. HibbelerPublisher:PEARSON Thermodynamics: An Engineering ApproachMechanical EngineeringISBN:9781259822674Author:Yunus A. Cengel Dr., Michael A. BolesPublisher:McGraw-Hill Education
Thermodynamics: An Engineering ApproachMechanical EngineeringISBN:9781259822674Author:Yunus A. Cengel Dr., Michael A. BolesPublisher:McGraw-Hill Education Control Systems EngineeringMechanical EngineeringISBN:9781118170519Author:Norman S. NisePublisher:WILEY
Control Systems EngineeringMechanical EngineeringISBN:9781118170519Author:Norman S. NisePublisher:WILEY Mechanics of Materials (MindTap Course List)Mechanical EngineeringISBN:9781337093347Author:Barry J. Goodno, James M. GerePublisher:Cengage Learning
Mechanics of Materials (MindTap Course List)Mechanical EngineeringISBN:9781337093347Author:Barry J. Goodno, James M. GerePublisher:Cengage Learning Engineering Mechanics: StaticsMechanical EngineeringISBN:9781118807330Author:James L. Meriam, L. G. Kraige, J. N. BoltonPublisher:WILEY
Engineering Mechanics: StaticsMechanical EngineeringISBN:9781118807330Author:James L. Meriam, L. G. Kraige, J. N. BoltonPublisher:WILEY





