McDougal Littell Jurgensen Geometry: Student Edition Geometry

5th Edition

ISBN: 9780395977279

Author: Ray C. Jurgensen, Richard G. Brown, John W. Jurgensen

Publisher: Houghton Mifflin Company College Division

See similar textbooks

Videos

Question

Chapter 1.3, Problem 14CE

(a)

To determine

The list of all the numbers between 1 and 2.

(a)

Expert Solution

Answer to Problem 14CE

There are infinite numbers between 1 and 2.

Explanation of Solution

Given information:

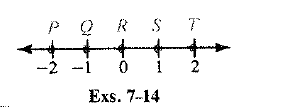
The graph is shown below as,

McDougal Littell Jurgensen Geometry: Student Edition Geometry, Chapter 1.3, Problem 14CE , additional homework tip 1

Formula used:

The rational and irrational numbers.

Calculation:

List all numbers between 1 and 2.

From the referred figure observe that,

There are infinite numbers between two numbers and on a number line every point is paired with a number and every number is paired with a point.

Because between any two number there are infinite rational and irrational numbers.

Therefore, from the above argument:

There are infinite numbers between 1 and 2.

Conclusion:

There are infinite numbers between 1 and 2.

(b)

To determine

To find: The point on the number line for every number between 1 and 2.

(b)

Expert Solution

Answer to Problem 14CE

A point on the number line for every number between 1 and 2 is possible.

Explanation of Solution

Given information:

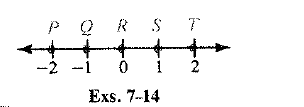
The graph is shown below as,

McDougal Littell Jurgensen Geometry: Student Edition Geometry, Chapter 1.3, Problem 14CE , additional homework tip 2

Formula used:

The rational and irrational numbers.

Calculation:

Find a point on the number line for every number between 1 and 2 if possible.

There are infinite numbers between two numbers and on a number line every point is paired with a number and every number is paired with a point.

Because between any two number there are infinite rational and irrational numbers.

Therefore from the above argument, it is clear that a point on the number line for every number between 1 and 2 is possible.

Conclusion:

A point on the number line for every number between 1 and 2 is possible.

(c)

To determine

The number of points between S and T.

(c)

Expert Solution

Answer to Problem 14CE

All the numbers between 1 and 2 are moving towards 2, thus numbers between 1 and 2 cannot be greater than 2.

Explanation of Solution

Given information:

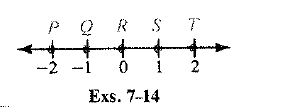
The graph is shown below as,

McDougal Littell Jurgensen Geometry: Student Edition Geometry, Chapter 1.3, Problem 14CE , additional homework tip 3

Formula used:

The infinite rational and irrational numbers are used.

Calculation:

Find the limit to the number of points between S and T if possible.

Because between any two numbers there are infinite rational and irrational numbers and the numbers are in increasing order.

All the numbers between 1 and 2 are moving towards 2, thus numbers between 1 and 2 cannot be greater than 2.

Conclusion:

All the numbers between 1 and 2 are moving towards 2, thus numbers between 1 and 2 cannot be greater than 2.

Chapter 1.3, Problem 13CE

Chapter 1.3, Problem 15CE

Chapter 1 Solutions

McDougal Littell Jurgensen Geometry: Student Edition Geometry

Ch. 1.1 - Prob. 1CE Ch. 1.1 - Prob. 2CE Ch. 1.1 - Prob. 3CE Ch. 1.1 - Prob. 4CE Ch. 1.1 - Prob. 5CE Ch. 1.1 - Prob. 6CE Ch. 1.1 - Prob. 7CE Ch. 1.1 - Prob. 8CE Ch. 1.1 - Prob. 1WE Ch. 1.1 - Prob. 2WE

Ch. 1.1 - Prob. 3WE Ch. 1.1 - Prob. 4WE Ch. 1.1 - Prob. 5WE Ch. 1.1 - Prob. 6WE Ch. 1.1 - Prob. 7WE Ch. 1.1 - Prob. 8WE Ch. 1.1 - Prob. 9WE Ch. 1.1 - Prob. 10WE Ch. 1.2 - Prob. 1CE Ch. 1.2 - Prob. 2CE Ch. 1.2 - Prob. 3CE Ch. 1.2 - Prob. 4CE Ch. 1.2 - Prob. 5CE Ch. 1.2 - Prob. 6CE Ch. 1.2 - Prob. 7CE Ch. 1.2 - Prob. 8CE Ch. 1.2 - Prob. 9CE Ch. 1.2 - Prob. 10CE Ch. 1.2 - Prob. 11CE Ch. 1.2 - Prob. 12CE Ch. 1.2 - Prob. 13CE Ch. 1.2 - Prob. 14CE Ch. 1.2 - Prob. 15CE Ch. 1.2 - Prob. 16CE Ch. 1.2 - Prob. 17CE Ch. 1.2 - Prob. 18CE Ch. 1.2 - Prob. 19CE Ch. 1.2 - Prob. 20CE Ch. 1.2 - Prob. 1WE Ch. 1.2 - Prob. 2WE Ch. 1.2 - Prob. 3WE Ch. 1.2 - Prob. 4WE Ch. 1.2 - Prob. 5WE Ch. 1.2 - Prob. 6WE Ch. 1.2 - Prob. 7WE Ch. 1.2 - Prob. 8WE Ch. 1.2 - Prob. 9WE Ch. 1.2 - Prob. 10WE Ch. 1.2 - Prob. 11WE Ch. 1.2 - Prob. 12WE Ch. 1.2 - Prob. 13WE Ch. 1.2 - Prob. 14WE Ch. 1.2 - Prob. 15WE Ch. 1.2 - Prob. 16WE Ch. 1.2 - Prob. 17WE Ch. 1.2 - Prob. 18WE Ch. 1.2 - Prob. 19WE Ch. 1.2 - Prob. 20WE Ch. 1.2 - Prob. 21WE Ch. 1.2 - Prob. 22WE Ch. 1.2 - Prob. 23WE Ch. 1.2 - Prob. 24WE Ch. 1.2 - Prob. 25WE Ch. 1.2 - Prob. 26WE Ch. 1.2 - Prob. 27WE Ch. 1.2 - Prob. 28WE Ch. 1.2 - Prob. 29WE Ch. 1.2 - Prob. 30WE Ch. 1.2 - Prob. 31WE Ch. 1.2 - Prob. 32WE Ch. 1.2 - Prob. 33WE Ch. 1.2 - Prob. 34WE Ch. 1.2 - Prob. 35WE Ch. 1.2 - Prob. 36WE Ch. 1.2 - Prob. 1ST1 Ch. 1.2 - Prob. 2ST1 Ch. 1.2 - Prob. 3ST1 Ch. 1.2 - Prob. 4ST1 Ch. 1.2 - Prob. 5ST1 Ch. 1.2 - Prob. 6ST1 Ch. 1.2 - Prob. 7ST1 Ch. 1.2 - Prob. 1AR Ch. 1.2 - Prob. 2AR Ch. 1.2 - Prob. 3AR Ch. 1.2 - Prob. 4AR Ch. 1.2 - Prob. 5AR Ch. 1.2 - Prob. 6AR Ch. 1.2 - Prob. 7AR Ch. 1.2 - Prob. 8AR Ch. 1.2 - Prob. 9AR Ch. 1.2 - Prob. 10AR Ch. 1.2 - Prob. 11AR Ch. 1.2 - Prob. 12AR Ch. 1.2 - Prob. 13AR Ch. 1.2 - Prob. 14AR Ch. 1.2 - Prob. 15AR Ch. 1.2 - Prob. 16AR Ch. 1.2 - Prob. 17AR Ch. 1.2 - Prob. 18AR Ch. 1.2 - Prob. 19AR Ch. 1.2 - Prob. 20AR Ch. 1.2 - Prob. 21AR Ch. 1.2 - Prob. 22AR Ch. 1.2 - Prob. 23AR Ch. 1.2 - Prob. 24AR Ch. 1.2 - Prob. 25AR Ch. 1.2 - Prob. 26AR Ch. 1.2 - Prob. 27AR Ch. 1.2 - Prob. 28AR Ch. 1.2 - Prob. 29AR Ch. 1.2 - Prob. 30AR Ch. 1.2 - Prob. 31AR Ch. 1.2 - Prob. 32AR Ch. 1.2 - Prob. 33AR Ch. 1.2 - Prob. 34AR Ch. 1.2 - Prob. 35AR Ch. 1.2 - Prob. 36AR Ch. 1.2 - Prob. 37AR Ch. 1.2 - Prob. 38AR Ch. 1.2 - Prob. 39AR Ch. 1.2 - Prob. 40AR Ch. 1.2 - Prob. 41AR Ch. 1.2 - Prob. 42AR Ch. 1.2 - Prob. 43AR Ch. 1.2 - Prob. 44AR Ch. 1.2 - Prob. 45AR Ch. 1.2 - Prob. 46AR Ch. 1.3 - Prob. 1CE Ch. 1.3 - Prob. 2CE Ch. 1.3 - Prob. 3CE Ch. 1.3 - Prob. 4CE Ch. 1.3 - Prob. 5CE Ch. 1.3 - Prob. 6CE Ch. 1.3 - Prob. 7CE Ch. 1.3 - Prob. 8CE Ch. 1.3 - Prob. 9CE Ch. 1.3 - Prob. 10CE Ch. 1.3 - Prob. 11CE Ch. 1.3 - Prob. 12CE Ch. 1.3 - Prob. 13CE Ch. 1.3 - Prob. 14CE Ch. 1.3 - Prob. 15CE Ch. 1.3 - Prob. 16CE Ch. 1.3 - Prob. 17CE Ch. 1.3 - Prob. 18CE Ch. 1.3 - Prob. 19CE Ch. 1.3 - Prob. 20CE Ch. 1.3 - Prob. 21CE Ch. 1.3 - Prob. 22CE Ch. 1.3 - Prob. 23CE Ch. 1.3 - Prob. 24CE Ch. 1.3 - Prob. 25CE Ch. 1.3 - Prob. 26CE Ch. 1.3 - Prob. 1WE Ch. 1.3 - Prob. 2WE Ch. 1.3 - Prob. 3WE Ch. 1.3 - Prob. 4WE Ch. 1.3 - Prob. 5WE Ch. 1.3 - Prob. 6WE Ch. 1.3 - Prob. 7WE Ch. 1.3 - Prob. 8WE Ch. 1.3 - Prob. 9WE Ch. 1.3 - Prob. 10WE Ch. 1.3 - Prob. 11WE Ch. 1.3 - Prob. 12WE Ch. 1.3 - Prob. 13WE Ch. 1.3 - Prob. 14WE Ch. 1.3 - Prob. 15WE Ch. 1.3 - Prob. 16WE Ch. 1.3 - Prob. 17WE Ch. 1.3 - Prob. 18WE Ch. 1.3 - Prob. 19WE Ch. 1.3 - Prob. 20WE Ch. 1.3 - Prob. 21WE Ch. 1.3 - Prob. 22WE Ch. 1.3 - Prob. 23WE Ch. 1.3 - Prob. 24WE Ch. 1.3 - Prob. 25WE Ch. 1.3 - Prob. 26WE Ch. 1.3 - Prob. 27WE Ch. 1.3 - Prob. 28WE Ch. 1.3 - Prob. 29WE Ch. 1.3 - Prob. 30WE Ch. 1.3 - Prob. 31WE Ch. 1.3 - Prob. 32WE Ch. 1.3 - Prob. 33WE Ch. 1.3 - Prob. 34WE Ch. 1.3 - Prob. 35WE Ch. 1.3 - Prob. 36WE Ch. 1.3 - Prob. 37WE Ch. 1.3 - Prob. 38WE Ch. 1.3 - Prob. 39WE Ch. 1.3 - Prob. 40WE Ch. 1.3 - Prob. 41WE Ch. 1.3 - Prob. 42WE Ch. 1.3 - Prob. 43WE Ch. 1.3 - Prob. 44WE Ch. 1.3 - Prob. 45WE Ch. 1.3 - Prob. 46WE Ch. 1.3 - Prob. 47WE Ch. 1.3 - Prob. 48WE Ch. 1.4 - Prob. 1CE Ch. 1.4 - Prob. 2CE Ch. 1.4 - Prob. 3CE Ch. 1.4 - Prob. 4CE Ch. 1.4 - Prob. 5CE Ch. 1.4 - Prob. 6CE Ch. 1.4 - Prob. 7CE Ch. 1.4 - Prob. 8CE Ch. 1.4 - Prob. 9CE Ch. 1.4 - Prob. 10CE Ch. 1.4 - Prob. 11CE Ch. 1.4 - Prob. 12CE Ch. 1.4 - Prob. 13CE Ch. 1.4 - Prob. 14CE Ch. 1.4 - Prob. 15CE Ch. 1.4 - Prob. 16CE Ch. 1.4 - Prob. 17CE Ch. 1.4 - Prob. 18CE Ch. 1.4 - Prob. 19CE Ch. 1.4 - Prob. 20CE Ch. 1.4 - Prob. 21CE Ch. 1.4 - Prob. 22CE Ch. 1.4 - Prob. 23CE Ch. 1.4 - Prob. 24CE Ch. 1.4 - Prob. 25CE Ch. 1.4 - Prob. 26CE Ch. 1.4 - Prob. 27CE Ch. 1.4 - Prob. 28CE Ch. 1.4 - Prob. 29CE Ch. 1.4 - Prob. 30CE Ch. 1.4 - Prob. 31CE Ch. 1.4 - Prob. 32CE Ch. 1.4 - Prob. 33CE Ch. 1.4 - Prob. 34CE Ch. 1.4 - Prob. 35CE Ch. 1.4 - Prob. 36CE Ch. 1.4 - Prob. 37CE Ch. 1.4 - Prob. 38CE Ch. 1.4 - Prob. 1WE Ch. 1.4 - Prob. 2WE Ch. 1.4 - Prob. 3WE Ch. 1.4 - Prob. 4WE Ch. 1.4 - Prob. 5WE Ch. 1.4 - Prob. 6WE Ch. 1.4 - Prob. 7WE Ch. 1.4 - Prob. 8WE Ch. 1.4 - Prob. 9WE Ch. 1.4 - Prob. 10WE Ch. 1.4 - Prob. 11WE Ch. 1.4 - Prob. 12WE Ch. 1.4 - Prob. 13WE Ch. 1.4 - Prob. 14WE Ch. 1.4 - Prob. 15WE Ch. 1.4 - Prob. 16WE Ch. 1.4 - Prob. 17WE Ch. 1.4 - Prob. 18WE Ch. 1.4 - Prob. 19WE Ch. 1.4 - Prob. 20WE Ch. 1.4 - Prob. 21WE Ch. 1.4 - Prob. 22WE Ch. 1.4 - Prob. 23WE Ch. 1.4 - Prob. 24WE Ch. 1.4 - Prob. 25WE Ch. 1.4 - Prob. 26WE Ch. 1.4 - Prob. 27WE Ch. 1.4 - Prob. 28WE Ch. 1.4 - Prob. 29WE Ch. 1.4 - Prob. 30WE Ch. 1.4 - Prob. 31WE Ch. 1.4 - Prob. 32WE Ch. 1.4 - Prob. 33WE Ch. 1.4 - Prob. 34WE Ch. 1.4 - Prob. 35WE Ch. 1.4 - Prob. 36WE Ch. 1.5 - Prob. 1CE Ch. 1.5 - Prob. 2CE Ch. 1.5 - Prob. 3CE Ch. 1.5 - Prob. 4CE Ch. 1.5 - Prob. 5CE Ch. 1.5 - Prob. 6CE Ch. 1.5 - Prob. 7CE Ch. 1.5 - Prob. 8CE Ch. 1.5 - Prob. 9CE Ch. 1.5 - Prob. 10CE Ch. 1.5 - Prob. 11CE Ch. 1.5 - Prob. 12CE Ch. 1.5 - Prob. 13CE Ch. 1.5 - Prob. 14CE Ch. 1.5 - Prob. 15CE Ch. 1.5 - Prob. 16CE Ch. 1.5 - Prob. 1WE Ch. 1.5 - Prob. 2WE Ch. 1.5 - Prob. 3WE Ch. 1.5 - Prob. 4WE Ch. 1.5 - Prob. 5WE Ch. 1.5 - Prob. 6WE Ch. 1.5 - Prob. 7WE Ch. 1.5 - Prob. 8WE Ch. 1.5 - Prob. 9WE Ch. 1.5 - Prob. 10WE Ch. 1.5 - Prob. 11WE Ch. 1.5 - Prob. 12WE Ch. 1.5 - Prob. 13WE Ch. 1.5 - Prob. 14WE Ch. 1.5 - Prob. 15WE Ch. 1.5 - Prob. 16WE Ch. 1.5 - Prob. 17WE Ch. 1.5 - Prob. 18WE Ch. 1.5 - Prob. 19WE Ch. 1.5 - Prob. 20WE Ch. 1.5 - Prob. 1E Ch. 1.5 - Prob. 2E Ch. 1.5 - Prob. 3E Ch. 1.5 - Prob. 4E Ch. 1.5 - Prob. 5E Ch. 1.5 - Prob. 6E Ch. 1.5 - Prob. 1ST2 Ch. 1.5 - Prob. 2ST2 Ch. 1.5 - Prob. 3ST2 Ch. 1.5 - Prob. 4ST2 Ch. 1.5 - Prob. 5ST2 Ch. 1.5 - Prob. 6ST2 Ch. 1.5 - Prob. 7ST2 Ch. 1.5 - Prob. 8ST2 Ch. 1.5 - Prob. 9ST2 Ch. 1.5 - Prob. 10ST2 Ch. 1.5 - Prob. 11ST2 Ch. 1.5 - Prob. 12ST2 Ch. 1 - Prob. 1CR Ch. 1 - Prob. 2CR Ch. 1 - Prob. 3CR Ch. 1 - Prob. 4CR Ch. 1 - Prob. 5CR Ch. 1 - Prob. 6CR Ch. 1 - Prob. 7CR Ch. 1 - Prob. 8CR Ch. 1 - Prob. 9CR Ch. 1 - Prob. 10CR Ch. 1 - Prob. 11CR Ch. 1 - Prob. 12CR Ch. 1 - Prob. 13CR Ch. 1 - Prob. 14CR Ch. 1 - Prob. 15CR Ch. 1 - Prob. 16CR Ch. 1 - Prob. 17CR Ch. 1 - Prob. 18CR Ch. 1 - Prob. 19CR Ch. 1 - Prob. 20CR Ch. 1 - Prob. 1CT Ch. 1 - Prob. 2CT Ch. 1 - Prob. 3CT Ch. 1 - Prob. 4CT Ch. 1 - Prob. 5CT Ch. 1 - Prob. 6CT Ch. 1 - Prob. 7CT Ch. 1 - Prob. 8CT Ch. 1 - Prob. 9CT Ch. 1 - Prob. 10CT Ch. 1 - Prob. 11CT Ch. 1 - Prob. 12CT Ch. 1 - Prob. 13CT Ch. 1 - Prob. 14CT Ch. 1 - Prob. 15CT Ch. 1 - Prob. 16CT Ch. 1 - Prob. 17CT Ch. 1 - Prob. 18CT Ch. 1 - Prob. 19CT Ch. 1 - Prob. 20CT Ch. 1 - Prob. 21CT Ch. 1 - Prob. 22CT Ch. 1 - Prob. 23CT Ch. 1 - Prob. 24CT

Additional Math Textbook Solutions

Find more solutions based on key concepts

Evaluate the integrals in Exercise 1–22. 7.

University Calculus: Early Transcendentals (4th Edition)

Ages A study of all the students at a small college showed a mean age of 20.7 and a standard deviation of 2.5 y...

Introductory Statistics

Testing Claims About Proportions. In Exercises 9-32, test the given claim. Identify the null hypothesis, altern...

Elementary Statistics (13th Edition)

Fill in each blank so that the resulting statement is true. If n is a counting number, bn, read ______, indicat...

College Algebra (7th Edition)

Fill in each blank so that the resulting statement is true. The quadratic function f(x)=a(xh)2+k,a0, is in ____...

Algebra and Trigonometry (6th Edition)

Find the point-slope form of the line passing through the given points. Use the first point as (x1, .y1). Plot ...

College Algebra with Modeling & Visualization (5th Edition)

Knowledge Booster

$Geometry$

Learn more about

Need a deep-dive on the concept behind this application? Look no further. Learn more about this topic, geometry and related others by exploring similar questions and additional content below.