
(a)
To find: the surface area of the cube.
(a)
Answer to Problem 15PPS
The surface area of the cube is
Explanation of Solution
Given:
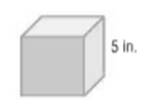
Formula used:
The surface area S of a square pyramid is S = L + 2B
Calculation:
The objective is to find the surface area of the cube.
The lateral area L of a square pyramid is given by the formula
L = Ph
Where P is the perimeter of the base and h is the height the square pyramid.
The surface area S of a square pyramid is given by the formula
S = L + 2B
Where L is the lateral surface area and B is the area of the base.
On combining the last two formulas, the surface area is given by
Find the surface area of the square box
Put side = 5 in the surface area formula to find the surface area of the cube.
Therefore, the surface area of the cube is
Conclusion:
Therefore, the surface area of the cube is
(b)
To complete: the given table.
(b)
Answer to Problem 15PPS
| Scale Factor of Dilation | Original | ||
| Length of Side | 5 | ||
| Surface Area |
Explanation of Solution
Given:
| Scale Factor of Dilation | Original | ||
| Length of Side | ■ | ■ | ■ |
| Surface Area | ■ | ■ | ■ |
Calculation:
Consider the table
| Scale Factor of Dilation | Original | ||
| Length of Side | 5 | ||
| Surface Area |
The objective is to complete the table.
Put side = 10 in the volume formula to find the surface area of the cube.
Therefore, the surface area of the cube is
Put side = 15 in the volume formula to find the surface area of the cube.
Therefore, the surface area of the cube is
Therefore, the complete table is
| Scale Factor of Dilation | Original | ||
| Length of Side | 5 | ||
| Surface Area |
Conclusion:
Therefore, the given table is completed.
(c)
To compare: the original surface area to the surface area after dilation.
(c)
Answer to Problem 15PPS
The new surface area is 4 times the original surface area when the scale factor is 2
The new surface area is 9 times the original surface area when the scale factor is 3
Explanation of Solution
The objective is to compare the original surface area to the surface are after dilation.
When the side of the cube is dilation by a scale factor 2 the new surface area is 4 times the original surface area.
When the side of the cube is dilation by a scale factor 3 the new surface area is 9 times the original surface area.
(d)
To explain:whether the same relationship exists with rectangular prism or not
(d)
Answer to Problem 15PPS
The same relation exist with the surface are of a rectangular prism
Explanation of Solution
Calculation:
The same relation exist with the surface are of a rectangular prism too because a cube is form of rectangle prism whose sides are equal.
The new surface area is the square of the scale factor of the side multiplied to the original surface area.
The original formula for surface area is
When length and width are double the new surface area becomes
Conclusion:
Therefore, the same relation exist with the surface are of a rectangular prism
Chapter 12 Solutions
Pre-Algebra, Student Edition
Additional Math Textbook Solutions
Introductory Statistics
Intro Stats, Books a la Carte Edition (5th Edition)
Elementary Statistics (13th Edition)
A Problem Solving Approach To Mathematics For Elementary School Teachers (13th Edition)
Calculus: Early Transcendentals (2nd Edition)
Elementary Statistics
- I need help explaining on this example on how can I define the Time-Domain Function, Apply the Laplace Transformation Formula, andarrow_forwardma Classes Term. Spring 2025 Title Details Credit Hours CRN Schedule Type Grade Mode Level Date Status Message *MATHEMATICS FOR MANAGEME... MTH 245, 400 4 54835 Online Normal Grading Mode Ecampus Undergradu... 03/21/2025 Registered **Web Registered... *SOIL SCIENCE CSS 205, 400 0 52298 Online Normal Grading Mode Undergraduate 03/21/2025 Waitlisted Waitlist03/21/2025 PLANT PATHOLOGY BOT 451, 400 4 56960 Online Normal Grading Mode Undergraduate 03/21/2025 Registered **Web Registered... Records: 3 Schedule Schedule Detailsarrow_forwardHere is an augmented matrix for a system of equations (three equations and three variables). Let the variables used be x, y, and z: 1 2 4 6 0 1 -1 3 0 0 1 4 Note: that this matrix is already in row echelon form. Your goal is to use this row echelon form to revert back to the equations that this represents, and then to ultimately solve the system of equations by finding x, y and z. Input your answer as a coordinate point: (x,y,z) with no spaces.arrow_forward
- 1 3 -4 In the following matrix perform the operation 2R1 + R2 → R2. -2 -1 6 After you have completed this, what numeric value is in the a22 position?arrow_forward5 -2 0 1 6 12 Let A = 6 7 -1 and B = 1/2 3 -14 -2 0 4 4 4 0 Compute -3A+2B and call the resulting matrix R. If rij represent the individual entries in the matrix R, what numeric value is in 131? Input your answer as a numeric value only.arrow_forward1 -2 4 10 My goal is to put the matrix 5 -1 1 0 into row echelon form using Gaussian elimination. 3 -2 6 9 My next step is to manipulate this matrix using elementary row operations to get a 0 in the a21 position. Which of the following operations would be the appropriate elementary row operation to use to get a 0 in the a21 position? O (1/5)*R2 --> R2 ○ 2R1 + R2 --> R2 ○ 5R1+ R2 --> R2 O-5R1 + R2 --> R2arrow_forward
- The 2x2 linear system of equations -2x+4y = 8 and 4x-3y = 9 was put into the following -2 4 8 augmented matrix: 4 -3 9 This augmented matrix is then converted to row echelon form. Which of the following matrices is the appropriate row echelon form for the given augmented matrix? 0 Option 1: 1 11 -2 Option 2: 4 -3 9 Option 3: 10 ܂ -2 -4 5 25 1 -2 -4 Option 4: 0 1 5 1 -2 Option 5: 0 0 20 -4 5 ○ Option 1 is the appropriate row echelon form. ○ Option 2 is the appropriate row echelon form. ○ Option 3 is the appropriate row echelon form. ○ Option 4 is the appropriate row echelon form. ○ Option 5 is the appropriate row echelon form.arrow_forwardLet matrix A have order (dimension) 2x4 and let matrix B have order (dimension) 4x4. What results when you compute A+B? The resulting matrix will have dimensions of 2x4. ○ The resulting matrix will be a single number (scalar). The resulting matrix will have dimensions of 4x4. A+B is undefined since matrix A and B do not have the same dimensions.arrow_forwardIf -1 "[a446]-[254] 4b = -1 , find the values of a and b. ○ There is no solution for a and b. ○ There are infinite solutions for a and b. O a=3, b=3 O a=1, b=2 O a=2, b=1 O a=2, b=2arrow_forward
- A student puts a 3x3 system of linear equations is into an augmented matrix. The student then correctly puts the augmented matrix into row echelon form (REF), which yields the following resultant matrix: -2 3 -0.5 10 0 0 0 -2 0 1 -4 Which of the following conclusions is mathematically supported by the work shown about system of linear equations? The 3x3 system of linear equations has no solution. ○ The 3x3 system of linear equations has infinite solutions. The 3x3 system of linear equations has one unique solution.arrow_forwardSolve the following system of equations using matrices: -2x + 4y = 8 and 4x - 3y = 9 Note: This is the same system of equations referenced in Question 14. If a single solution exists, express your solution as an (x,y) coordinate point with no spaces. If there are infinite solutions write inf and if there are no solutions write ns in the box.arrow_forwardI need help explaining on this examplearrow_forward
 Algebra and Trigonometry (6th Edition)AlgebraISBN:9780134463216Author:Robert F. BlitzerPublisher:PEARSON
Algebra and Trigonometry (6th Edition)AlgebraISBN:9780134463216Author:Robert F. BlitzerPublisher:PEARSON Contemporary Abstract AlgebraAlgebraISBN:9781305657960Author:Joseph GallianPublisher:Cengage Learning
Contemporary Abstract AlgebraAlgebraISBN:9781305657960Author:Joseph GallianPublisher:Cengage Learning Linear Algebra: A Modern IntroductionAlgebraISBN:9781285463247Author:David PoolePublisher:Cengage Learning
Linear Algebra: A Modern IntroductionAlgebraISBN:9781285463247Author:David PoolePublisher:Cengage Learning Algebra And Trigonometry (11th Edition)AlgebraISBN:9780135163078Author:Michael SullivanPublisher:PEARSON
Algebra And Trigonometry (11th Edition)AlgebraISBN:9780135163078Author:Michael SullivanPublisher:PEARSON Introduction to Linear Algebra, Fifth EditionAlgebraISBN:9780980232776Author:Gilbert StrangPublisher:Wellesley-Cambridge Press
Introduction to Linear Algebra, Fifth EditionAlgebraISBN:9780980232776Author:Gilbert StrangPublisher:Wellesley-Cambridge Press College Algebra (Collegiate Math)AlgebraISBN:9780077836344Author:Julie Miller, Donna GerkenPublisher:McGraw-Hill Education
College Algebra (Collegiate Math)AlgebraISBN:9780077836344Author:Julie Miller, Donna GerkenPublisher:McGraw-Hill Education





