Chapter 12, Problem 43RE

(a)

To determine

To approximate: the limit by using a graphing utility to graph the function..

Explanation of Solution

Given information:

Given following limit

  $\underset{x\to 1^{+}}{\lim }\frac{\sqrt{2x+1}-\sqrt{3}}{x-1}$

Calculation:

Let $f\left(x\right)=\frac{\sqrt{2x+1}-\sqrt{3}}{x-1}$ and plot the function $f\left(x\right)$ .

To calculate the model using the T1-83 graphing calculator follows the steps:

Press $Y=$ and enter the equation

  

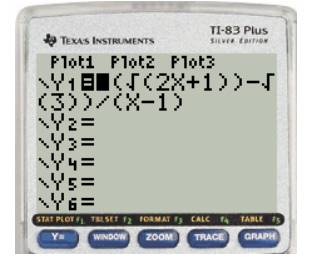
Press ZOOM and choose the appropriate zoom function, then plot window is like this

  

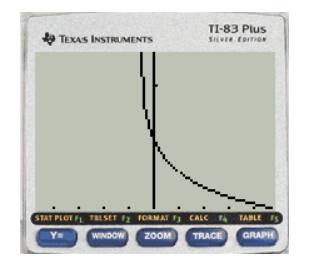
From the graph we can see that the function converges to a single bounded value as it approaches 1from right side..

(b)

To determine

To approximate: the limit by using the table feature of the graphing utility to create a table.

Answer to Problem 43RE

Limit converges to a value of 0.577.

Explanation of Solution

Calculation:

Numerically approximate the limit using $f\left(x\right)=\frac{\sqrt{2x+1}-\sqrt{3}}{x-1}$ and tabulate it using the T1-83 graphing calculator, with following steps:

Press Y= and enter the equation

  

Press $2^{nd}$ key and window to set table

  

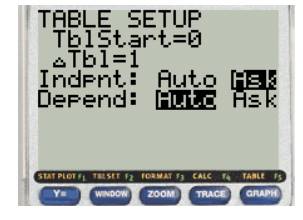
Press $2^{nd}$ key and graph button and enter the values of $x$ :

  

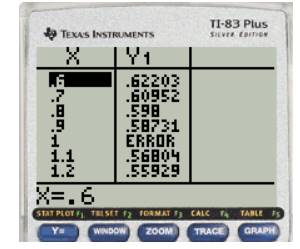
Limit converges to a value of 0.577.