
ToEvaluate:Thederivative of
Answer to Problem 60E
The derivative of
The point on the graph of
From the graph of
Explanation of Solution
Given:
The function
Concept Used:
The derivative of
The tangent line is horizontal when the slope of tangent line is zero.
The equation of the tangent line to the graph of a function
Calculation:
Forthe function
The derivative of
Therefore, the derivative of
The tangent line is horizontal when the slope of tangent line is zero.
Since the derivative of a function is the slope of its tangent line.
Substituting the derivative of
Substituting in the function
Therefore, the point on the graph of
For the equation of tangent line
Since, the tangent line is horizontal, so the slope of tangent line is
The point on the tangent line is
The equation of the tangent line to the graph of a function
Plotting tangent line and the graph of
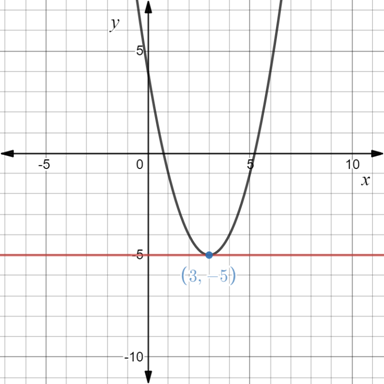
Therefore, from the above graph, it is verified that the point on the graph of
Conclusion:
Thederivative of
The point on the graph of
From the graph of
Chapter 12 Solutions
Precalculus with Limits
- on donne f(x) da fonction derive dhe do fonction fcsos calcule f'(x) orans chacun des Cas sulants: 3 1) f(x)=5x-11, 2- f (x) = ->³ 3-1(x) = x² 12x +π; 4-f(x)=- 5-f(x) = 33-4x6-609)=-3x²+ 7= f(x) = x + 1.8-f(x) = 4 s-f(x) = x++ X+1 -x-1 2 I 3x-4 девоarrow_forwardThe correct answer is Ccould you show me how to do it by finding a0 and and akas well as setting up the piecewise function and integratingarrow_forwardT 1 7. Fill in the blanks to write the calculus problem that would result in the following integral (do not evaluate the interval). Draw a graph representing the problem. So π/2 2 2πxcosx dx Find the volume of the solid obtained when the region under the curve on the interval is rotated about the axis.arrow_forward
- 38,189 5. Draw a detailed graph to and set up, but do not evaluate, an integral for the volume of the solid obtained by rotating the region bounded by the curve: y = cos²x_for_ |x| ≤ and the curve y y = about the line x = =플 2 80 F3 a FEB 9 2 7 0 MacBook Air 3 2 stv DGarrow_forwardFind f(x) and g(x) such that h(x) = (fog)(x) and g(x) = 3 - 5x. h(x) = (3 –5x)3 – 7(3 −5x)2 + 3(3 −5x) – 1 - - - f(x) = ☐arrow_forwardx-4 Let f(x)=5x-1, h(x) = Find (fo h)(0). 3 (fo h)(0) = (Type an integer or a fraction.)arrow_forward
- Fill in the blanks to write the calculus problem that would result in the following integral (do not evaluate the interval). Draw a graph representing the problem. π/2 So/² 2xcosx dx Find the volume of the solid obtained when the region under the curve 38,189 on the interval is rotated about the axis.arrow_forwardLet f(x) = -5x-1, g(x) = x² + 5, h(x) = · x+4 3 Find (hog of)(1). (hogof)(1)= (Simplify your answer. Type an integer or a decimal.)arrow_forwardFor the given function, find (a) the equation of the secant line through the points where x has the given values and (b) the equation of the tangent line when x has the first value. y= f(x) = x²+x; x=-1,x=2 a. Which of the following formulas can be used to find the slope of the secant line? ○ A. 2-(-1) f(2) f(-1) 2+(-1) C. 1(2)+(-1) The equation of the secant line is 1(2)+(-1) О в. 2+(-1) f(2)-(-1) D. 2-(-1)arrow_forward
 Calculus: Early TranscendentalsCalculusISBN:9781285741550Author:James StewartPublisher:Cengage Learning
Calculus: Early TranscendentalsCalculusISBN:9781285741550Author:James StewartPublisher:Cengage Learning Thomas' Calculus (14th Edition)CalculusISBN:9780134438986Author:Joel R. Hass, Christopher E. Heil, Maurice D. WeirPublisher:PEARSON
Thomas' Calculus (14th Edition)CalculusISBN:9780134438986Author:Joel R. Hass, Christopher E. Heil, Maurice D. WeirPublisher:PEARSON Calculus: Early Transcendentals (3rd Edition)CalculusISBN:9780134763644Author:William L. Briggs, Lyle Cochran, Bernard Gillett, Eric SchulzPublisher:PEARSON
Calculus: Early Transcendentals (3rd Edition)CalculusISBN:9780134763644Author:William L. Briggs, Lyle Cochran, Bernard Gillett, Eric SchulzPublisher:PEARSON Calculus: Early TranscendentalsCalculusISBN:9781319050740Author:Jon Rogawski, Colin Adams, Robert FranzosaPublisher:W. H. Freeman
Calculus: Early TranscendentalsCalculusISBN:9781319050740Author:Jon Rogawski, Colin Adams, Robert FranzosaPublisher:W. H. Freeman
 Calculus: Early Transcendental FunctionsCalculusISBN:9781337552516Author:Ron Larson, Bruce H. EdwardsPublisher:Cengage Learning
Calculus: Early Transcendental FunctionsCalculusISBN:9781337552516Author:Ron Larson, Bruce H. EdwardsPublisher:Cengage Learning





