Chapter 11.4, Problem 1MP

a.

To determine

The least common denominator for the two terms of the expression of surface area of the lunch box.

Answer to Problem 1MP

  $x$

Explanation of Solution

Given:

The volume of the lunch box is, $355\text{in}{\text{.}}^3$

  

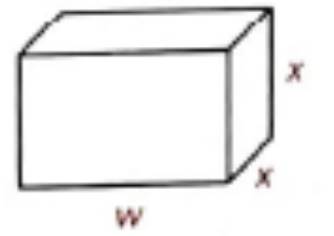
Concept Used:

• Least Common Denominator (LCD) is the smallest number that is divisible by the denominator of all the fractions that are being added or subtracted.
• Solving an equation containing rational expressions
1. Multiply both sides of equations by LCD(least common denominator) of all denominators.
2. Remove any grouping symbols and solve the resulting equation for the variable asked in equation

Calculation:

The surface area of the lunch box is given by,

  $S=2x^2+4wx\mathrm{......}\left(i\right)$

And the volume of the box is given by,

  $\begin{array}{c}V=w\cdot x\cdot x\\ V=w{x}^2\\ 355=w{x}^2\\ \Rightarrow w=\frac{355}{x^2}\end{array}$

Substitute this value of w in ( i ) to get

  $\begin{array}{l}S=2x^2+4\left(\frac{355}{x^2}\right)x\\ S=2x^2+\frac{1420}{x}\end{array}$

So, in the expression of surface area, the first term has no denominator, so it can be considered 1 as its denominator. The denominator of second term is x , so the least common denominator of 1 and x should be x .

Thus, the least common denominator of the two terms of the expression of surface area is x .

b.

To determine

The expression for the surface area of the lunch box as a single rational expression.

Answer to Problem 1MP

  $\frac{2x^3+1420}{x}$

Explanation of Solution

Given:

The volume of the lunch box is, $355\text{in}{\text{.}}^3$

  

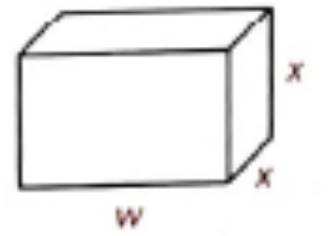
Concept Used:

• Least Common Denominator (LCD) is the smallest number that is divisible by the denominator of all the fractions that are being added or subtracted.
• Solving an equation containing rational expressions
3. Multiply both sides of equations by LCD(least common denominator) of all denominators.
4. Remove any grouping symbols and solve the resulting equation for the variable asked in equation

Calculation:

The expression for the surface area of the lunch box is given by,

  $S=2x^2+\frac{1420}{x}$

So, in the expression of surface area, the first term has no denominator, so it can be considered 1 as its denominator. The denominator of second term is x , so the least common denominator of 1 and x should be x . So, multiply the first term by x up and down and then simplify the numerators over the common denominator as shown below,

  $\begin{array}{l}S=2x^2\cdot \frac{x}{x}+\frac{1420}{x}\\ S=\frac{2x^3}{x}+\frac{1420}{x}\\ S=\frac{2x^3+1420}{x}\end{array}$

Thus, the single rational expression for the surface area is $\frac{2x^3+1420}{x}$ .