Chapter 11.3, Problem 5CYU

(a)

To determine

To find: The relative frequency table showing the theoretical probabilities.

Answer to Problem 5CYU

Therelative frequency table is shown in table 1

Explanation of Solution

Given:

The given figure is shown in Figure 1

  

Figure 1

Calculation:

Consider the random variable is X that represents the sum of the values of two spins of the spinning wheels.

The minimum value of the wheel is 2 and maximum is 12, the X can take any value 4 to 24. Thus, the even space of the random variable is,

  $S=\left\{4,6,7,8,9,\mathrm{.......},19,20,22,24\right\}$

Consider the definition of the theatrical probability as,

  $P\left(X\right)=\frac{\text{total}\text{number}\text{of}\text{favourable}\text{event}}{\text{Total}\text{number}\text{of}\text{event}}$

The random variable can take any value of 4 in one ways as 2 in spin 1 and 2 in spin 2.

The wheel spun the number that can appear are $\left\{2,4,5,6,7,8,10,12\right\}$ . This is the total number of event that corresponds to each of the spun is 8. Here, the area of each sector is neglected as each of the sector looks same to each other thus,

  $P\left(2\text{in}1\text{st}\text{spin}\right)=\frac{1}{8}$

And,

  $P\left(2\text{in}{2}^{\text{nd}}\text{spin}\right)=\frac{1}{8}$

Hence,

  $\begin{array}{c}P\left(X=4\right)=\left(\frac{1}{8}\right)\left(\frac{1}{8}\right)\\ =\frac{1}{64}\end{array}$

Similarly the random variable X can take the value 6 in two ways as,

1st spin	2	4
2nd spin	4	2

Then, the probability is,

  $\begin{array}{c}P\left(6\right)=\left(\frac{1}{8}\right)\left(\frac{1}{8}\right)+\left(\frac{1}{8}\right)\left(\frac{1}{8}\right)\\ =\frac{1}{32}\end{array}$

Similarly the random variable X can take the value 12 in two ways as,

1st spin	2	5	4	8	6	10	2
2nd spin	5	2	8	4	6	2	10

Then, the probability is,

  $\begin{array}{c}P\left(12\right)=\left(\frac{1}{8}\right)\left(\frac{1}{8}\right)+\left(\frac{1}{8}\right)\left(\frac{1}{8}\right)+\left(\frac{1}{8}\right)\left(\frac{1}{8}\right)+\left(\frac{1}{8}\right)\left(\frac{1}{8}\right)\\ =\frac{7}{64}\end{array}$

Similarly the random variable X can take the value 20 in two ways as,

1st spin	10	12	8
2nd spin	10	8	12

Then, the probability is,

  $\begin{array}{c}P\left(20\right)=\left(\frac{1}{8}\right)\left(\frac{1}{8}\right)+\left(\frac{1}{8}\right)\left(\frac{1}{8}\right)+\left(\frac{1}{8}\right)\left(\frac{1}{8}\right)\\ =\frac{3}{64}\end{array}$

Thus, the relative frequency table is shown in Table 1

Table 1

$X=x_i$	Frequency	$P\left(X=x_i\right)$
4	1	$\frac{1}{64}$
6	2
7	2	$\frac{1}{32}$
8	3	$\frac{3}{64}$

(b)

To determine

To find: The graph for the theoretical probability distribution.

Answer to Problem 5CYU

Thegraph is shown in Figure 1

Explanation of Solution

Calculation:

From the theoretical data shown in Table 1 the graph for the data is shown in Figure 2

  

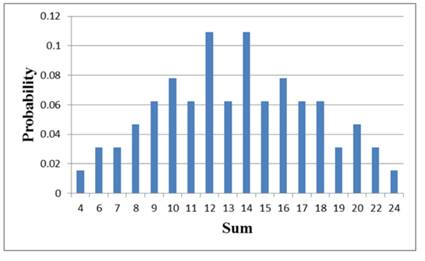
Figure 2

(c)

To determine

To find: The relative frequency table for 100 trials.

Answer to Problem 5CYU

The relative frequency table is shown in table 2

Explanation of Solution

Perform 100 trials of the spinning the wheel two times and record the sum of the values and its frequency. The calculate the corresponding probability using the same concept as mentioned in part (a)

The required table is shown in Table 2

Table 2

$X=x_i$	Frequency	$P\left(X=x_i\right)$
4	1	$\frac{1}{64}$
6	1	$\frac{1}{64}$
7	3	$\frac{3}{64}$
8	3	$\frac{3}{64}$
9	2	$\frac{1}{32}$
10	6	$\frac{3}{32}$
11	5	$\frac{5}{64}$
12	7	$\frac{7}{64}$
13	5	$\frac{5}{64}$
14	3	$\frac{1}{8}$
15	3	$\frac{3}{64}$
16	3	$\frac{3}{64}$
17	4	$\frac{1}{16}$
18	5	$\frac{5}{64}$
19	2	$\frac{1}{32}$
20	3	$\frac{3}{64}$
22	2	$\frac{1}{32}$
24	1	$\frac{1}{64}$

(d)

To determine

To find: The relative frequency table showing the theoretical probabilities.

Answer to Problem 5CYU

The relative frequency table is shown in table 1

Explanation of Solution

From the theoretical data shown in Table 1 the graph for the data is shown in Figure 3

  

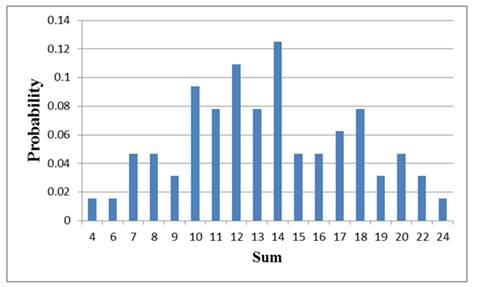
Figure 3

(e)

To determine

To find: The expected value of the random variable X .

Answer to Problem 5CYU

Thevalue of the random variable is $13.5$ .

Explanation of Solution

Consider the formula to determine the expected value of the random variable is,

  $E\left(X\right)={\displaystyle \sum _{i=1}^{n}P\left(X=x_i\right)}$

Then,

  $\begin{array}{c}E\left(X\right)=\left(\begin{array}{l}4\left(\frac{1}{64}\right)+6\left(\frac{1}{32}\right)+8\left(\frac{3}{64}\right)+10\left(\frac{5}{64}\right)+11\left(\frac{1}{16}\right)+\\ 12\left(\frac{7}{64}\right)+13\left(\frac{1}{16}\right)+14\left(\frac{7}{64}\right)+15\left(\frac{1}{16}\right)+16\left(\frac{5}{64}\right)\\ 17\left(\frac{1}{16}\right)+18\left(\frac{1}{16}\right)+16\left(\frac{1}{32}\right)+20\left(\frac{3}{64}\right)+22\left(\frac{1}{32}\right)\\ +24\left(\frac{1}{64}\right)\end{array}\right)\backslash \\ =13.5\end{array}$

(f)

To determine

To find: The standard deviation of the random variable X.

Answer to Problem 5CYU

The value of the standard deviation is $4.2866$ .

Explanation of Solution

Consider the formula to determine standard deviation of the random variable X is,

  $\sigma =\sqrt{{\displaystyle \sum _{i=1}^n\left[x_i-E\left(X\right)\right]P\left(x=x_i\right)}}$

Therefore,

  $\begin{array}{l}{\sigma }^2=\left(\begin{array}{l}{\left(4-13.5\right)}^{2}P\left(X=4\right)+\left(6-13.5\right)P\left(X=6\right)+\mathrm{...}\\ +{\left(22-13.5\right)}^{2}P\left(X=22\right)+{\left(24-13.5\right)}^2\left(X=24\right)\end{array}\right)\\ {\sigma }^2=18.3750\\ \sigma =4.2866\end{array}$